Positieve correlatie

In dit artikel leer je wat positieve correlatie betekent in de statistiek, voorbeelden van variabelen met positieve correlatie en wat de verschillen zijn tussen andere soorten correlatie.

Wat is een positieve correlatie?

In de statistieken is een positieve correlatie een soort correlatie tussen twee verschillende variabelen. Meer specifiek betekent een positieve correlatie tussen twee variabelen dat als de waarde van de ene variabele toeneemt, de andere variabele ook toeneemt.

Om een correlatie tussen twee variabelen als positief te beschouwen, moet de waarde van de correlatiecoëfficiënt tussen 0 (niet inbegrepen) en 1 (inclusief) liggen.

Merk op dat positieve correlatie ook directe correlatie kan worden genoemd.

Voorbeeld van positieve correlatie

Gezien de definitie van positieve correlatie, vindt u hieronder een voorbeeld van twee variabelen die een dergelijke correlatie vertonen.

• In de volgende frequentietabel zijn de wiskunde- en statistiekscores van een steekproef van twintig leerlingen als gegevens verzameld. Analyseer de relatie tussen de twee variabelen.

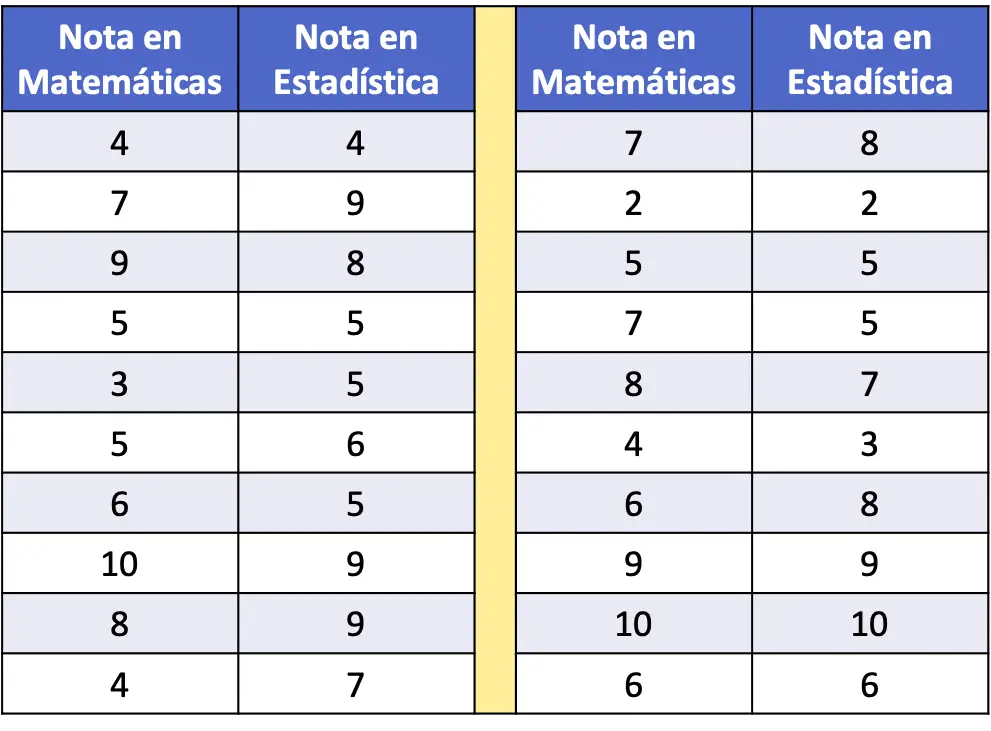
Voordat de correlatiecoëfficiënt wordt berekend, wordt aanbevolen om eerst de statistische gegevensset weer te geven in een spreidingsdiagram voor voorlopig onderzoek.

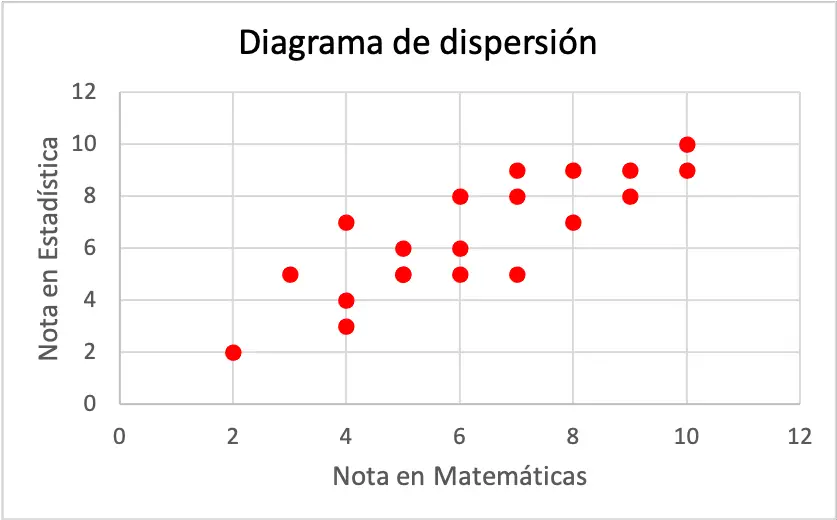
Zoals de grafiek laat zien, lijkt het erop dat de twee variabelen een positieve lineaire correlatie hebben, aangezien naarmate het wiskundecijfer stijgt, het statistiekcijfer ook toeneemt. Maar om met zekerheid het type correlatie te bepalen, is het noodzakelijk om de correlatiecoëfficiënt te berekenen :

De waarde van de Pearson-correlatiecoëfficiënt is groter dan 0 en zeer dicht bij 1, de correlatie tussen de twee onderzochte variabelen is dus inderdaad positief.

Interpretatie van positieve correlatie

Om het begrip van de betekenis van positieve correlatie in statistieken af te ronden, zullen we in deze sectie zien hoe we de waarde van een positieve correlatie tussen twee variabelen kunnen interpreteren.

Hoe hoger de waarde van de correlatiecoëfficiënt, hoe meer de twee variabelen positief gecorreleerd zijn. Dus als de waarde van de correlatiecoëfficiënt dicht bij 1 ligt, betekent dit dat de correlatie tussen de twee variabelen positief en zeer sterk is.

Aan de andere kant, wanneer de waarde van de correlatiecoëfficiënt laag is en bijna nul, betekent dit dat de correlatie tussen de twee variabelen positief maar zwak is. Zelfs als de correlatiecoëfficiënt nul of negatief wordt, betekent dit dat de correlatie respectievelijk nul of negatief is. Hieronder zullen we de verschillen tussen deze drie soorten correlatie zien.

Ten slotte moet worden opgemerkt dat een positieve correlatie geen oorzakelijk verband tussen de variabelen impliceert. Dat wil zeggen: als twee variabelen een positieve correlatie hebben, betekent dit dat ze lineair gerelateerd zijn, maar dat de ene variabele niet noodzakelijkerwijs de oorzaak is van de andere.

Net als in de vorige sectie zijn cijfers voor wiskunde en statistiek positief gecorreleerd, maar het behalen van een goed cijfer voor wiskunde garandeert niet automatisch een goed cijfer voor statistiek; beide vakken moeten eerder worden bestudeerd. Concluderend: het cijfer voor wiskunde is niet de oorzaak van het cijfer voor statistiek; de twee variabelen zijn eenvoudigweg met elkaar verbonden.

Positieve, negatieve en nulcorrelatie

Naast een positieve correlatie kunnen twee variabelen in de statistieken ook een negatieve of nulcorrelatie hebben. Daarom zullen we in deze sectie zien hoe deze drie soorten correlaties worden onderscheiden.

• Positieve correlatie : de ene variabele neemt toe als de andere ook toeneemt. De waarde van de correlatiecoëfficiënt ligt tussen 0 (niet inbegrepen) en 1 (inclusief).
• Negatieve correlatie : wanneer de ene variabele toeneemt, neemt de andere af, en omgekeerd: als de ene variabele afneemt, neemt de andere toe. De waarde van de correlatiecoëfficiënt ligt tussen -1 (inclusief) en 0 (niet inclusief).
• Nulcorrelatie : er is geen verband tussen de twee variabelen. De correlatiecoëfficiënt is gelijk aan 0.

In de volgende grafieken ziet u elk type correlatie weergegeven: