Posterieure waarschijnlijkheid: definitie + voorbeeld

De a posteriori waarschijnlijkheid is de bijgewerkte waarschijnlijkheid dat een gebeurtenis zal plaatsvinden nadat rekening is gehouden met nieuwe informatie.

We zouden bijvoorbeeld geïnteresseerd kunnen zijn in de waarschijnlijkheid dat een gebeurtenis „A“ zal plaatsvinden nadat we rekening hebben gehouden met een gebeurtenis „B“ die zojuist heeft plaatsgevonden. We kunnen deze posterieure waarschijnlijkheid berekenen met behulp van de volgende formule:

P(A|B) = P(A) * P(B|A) / P(B)

Goud:

P(A|B) = de waarschijnlijkheid dat gebeurtenis A zal plaatsvinden, gegeven dat gebeurtenis B heeft plaatsgevonden. Merk op dat “| » betekent “gegeven”.

P(A) = de waarschijnlijkheid dat gebeurtenis A zal plaatsvinden.

P(B) = de waarschijnlijkheid dat gebeurtenis B zal plaatsvinden.

P(B|A) = de waarschijnlijkheid dat gebeurtenis B zal plaatsvinden, gegeven dat gebeurtenis A heeft plaatsgevonden.

Voorbeeld: Berekening van de posterieure waarschijnlijkheid

Een bos bestaat voor 20% uit eiken en voor 80% uit esdoorns. Stel dat we weten dat 90% van de eikenbomen gezond is, terwijl slechts 50% van de esdoorns gezond is. Stel dat je van een afstand kunt zien dat een bepaalde boom gezond is. Hoe groot is de kans dat de boom een eik is?

Bedenk dat de waarschijnlijkheid dat gebeurtenis A zal plaatsvinden, gegeven dat gebeurtenis B heeft plaatsgevonden, gelijk is aan:

P(A|B) = P(A) * P(B|A) / P(B)

In dit voorbeeld is de kans dat de boom een eik is, gegeven dat de boom gezond is,:

P(Eiken|Gezond) = P(Eiken) * P(Gezond|Eiken) / P(Gezond)

P(Eik) = De kans dat een bepaalde boom een eik is, is 0,2 omdat 20% van alle bomen in het bos eiken zijn.

P(Gezond) = De kans dat een bepaalde boom gezond is, kan als volgt worden berekend: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Gezond|Eik) = De kans dat een boom gezond is, gegeven het feit dat het een eik is, is 0,9 , aangezien ons is verteld dat 90% van de eiken gezond is.

Met behulp van deze drie getallen kunnen we de waarschijnlijkheid bepalen dat de boom een eik is, gegeven dat hij gezond is:

P(Eiken|Gezond) = P(Eiken) * P(Gezond|Eiken) / P(Gezond) = (0,2) * (0,9) / (0,58) = 0,3103 .

Laten we, voor een intuïtief begrip van deze waarschijnlijkheid, aannemen dat het volgende raster dit bos van 100 bomen voorstelt. Precies 20 van de bomen zijn eiken en 18 daarvan zijn gezond. De overige 80 bomen zijn esdoorns en 40 daarvan zijn gezond.

(O = Eik, M = Esdoorn, Groen = Gezond, Rood = Ongezond)

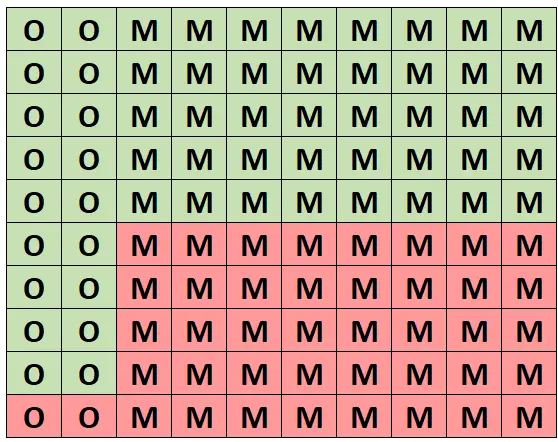
Van alle bomen zijn er precies 58 gezond en 18 van die gezonde bomen zijn eiken. Dus als we weten dat we een gezonde boom hebben geselecteerd, is de kans dat het een eik is 18/58 = 0,3103 .

Wanneer moet je posterieure waarschijnlijkheid gebruiken?

Posterieure waarschijnlijkheid wordt gebruikt op een breed scala aan gebieden, waaronder financiën, geneeskunde, economie en weersvoorspellingen.

Het punt van het gebruik van posterieure waarschijnlijkheden is het actualiseren van een eerdere overtuiging die we ergens over hadden zodra we nieuwe informatie verkrijgen.

Bedenk uit het vorige voorbeeld dat we wisten dat de kans dat een bepaalde boom in het bos een eik was, 20% was. Dit wordt een voorafgaande waarschijnlijkheid genoemd. Als we gewoon willekeurig een boom zouden kiezen, wisten we dat de kans dat het een eik was 0,20 was.

Toen we echter de nieuwe informatie kregen dat de door ons geselecteerde boom gezond was, konden we deze nieuwe informatie gebruiken om vast te stellen dat de posterieure waarschijnlijkheid dat deze boom een eik was, in plaats daarvan 0,3103 was.

In de echte wereld ontdekken mensen voortdurend nieuwe informatie. Deze nieuwe informatie helpt ons onze eerdere overtuigingen bij te werken. In statistische termen betekent dit dat we in staat zijn om latere waarschijnlijkheden te genereren van gebeurtenissen die plaatsvinden, wat ons helpt een nauwkeuriger inzicht in de wereld te krijgen en ons in staat stelt nauwkeurigere voorspellingen te doen over toekomstige gebeurtenissen.