Hoe u een puntproduct kunt berekenen op een ti-84-rekenmachine
Gegeven de vector a = [a 1 , a 2 , a 3 ] en de vector b = [b 1 , b 2 , b 3 ], wordt het scalaire product van de vector a en de vector b, aangeduid als ab , gegeven door:
ab = een 1 * b 1 + een 2 * b 2 + een 3 * b 3
Als a = [2, 5, 6] en b = [4, 3, 2] bijvoorbeeld, dan zou het puntproduct van a en b gelijk zijn aan:
ab = 2*4 + 5*3 + 6*2
ab = 8 + 15 + 12
ab = 35
We kunnen de volgende syntaxis gebruiken om het puntproduct van twee vectoren op een TI-84-rekenmachine te berekenen:
sum ({2, 5, 6} * {4, 3, 2})
Het volgende stapsgewijze voorbeeld laat zien hoe u deze syntaxis in de praktijk kunt gebruiken.
Voorbeeld: Bereken het puntproduct op de TI-84-rekenmachine
Volg de volgende stappen om het puntproduct tussen twee vectoren te berekenen:
Stap 1: Voer de opdracht sum(.
Druk eerst op 2nd en vervolgens op STAT , blader vervolgens naar MATH en druk op sum :
Stap 2: Voer de linker accolade in.
Druk vervolgens op 2nd en vervolgens op ( om de eerste accolade in te voeren:
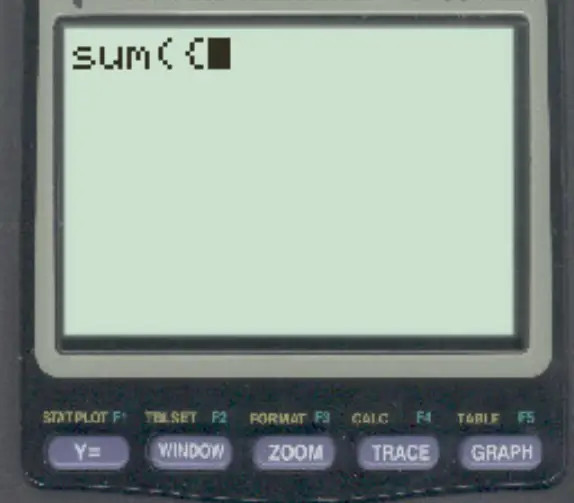
Stap 3: Voer de gegevens in
Voer vervolgens voor elke vector de volgende waarden in:
- Vector a: 2, 5, 6
- Vectorb: 4, 3, 2
Zorg ervoor dat u een vermenigvuldigingsteken tussen de twee vectoren plaatst en sluit het einde van de opdracht sum() af met een haakje rechts. Druk vervolgens op ENTER :
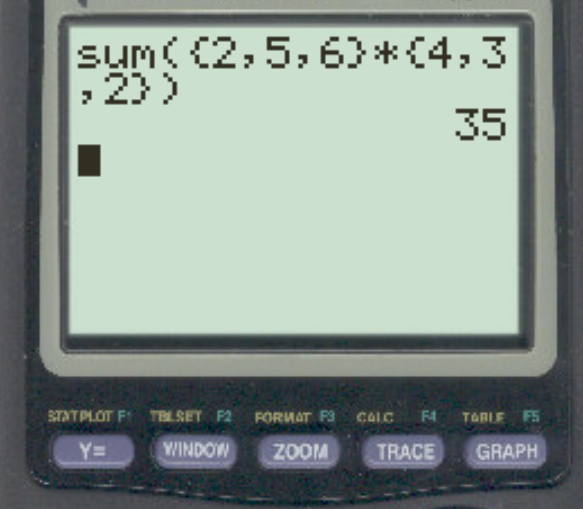
Het puntproduct blijkt 35 te zijn. Dit komt overeen met de waarde die we handmatig hebben berekend.
Aanvullende bronnen
Hoe het puntproduct in Excel te berekenen
Hoe u een puntproduct in Google Spreadsheets kunt berekenen
Hoe het puntproduct in R te berekenen
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder