Normaliteit testen in python (4 methoden)

Veel statistische tests gaan ervan uit dat datasets normaal verdeeld zijn.

Er zijn vier veelgebruikte manieren om deze hypothese in Python te controleren:

1. (Visuele methode) Maak een histogram.

• Als het histogram ongeveer de vorm van een klok heeft, wordt aangenomen dat de gegevens normaal verdeeld zijn.

2. (Visuele methode) Maak een QQ-plot.

• Als de punten op de grafiek grofweg langs een rechte diagonale lijn liggen, wordt aangenomen dat de gegevens normaal verdeeld zijn.

3. (Formele statistische test) Voer een Shapiro-Wilk-test uit.

• Als de p-waarde van de test groter is dan α = 0,05, wordt aangenomen dat de gegevens normaal verdeeld zijn.

4. (Formele statistische test) Voer een Kolmogorov-Smirnov-test uit.

• Als de p-waarde van de test groter is dan α = 0,05, wordt aangenomen dat de gegevens normaal verdeeld zijn.

De volgende voorbeelden laten zien hoe u elk van deze methoden in de praktijk kunt gebruiken.

Methode 1: Maak een histogram

De volgende code laat zien hoe u een histogram maakt voor een gegevensset die een lognormale verdeling volgt:

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

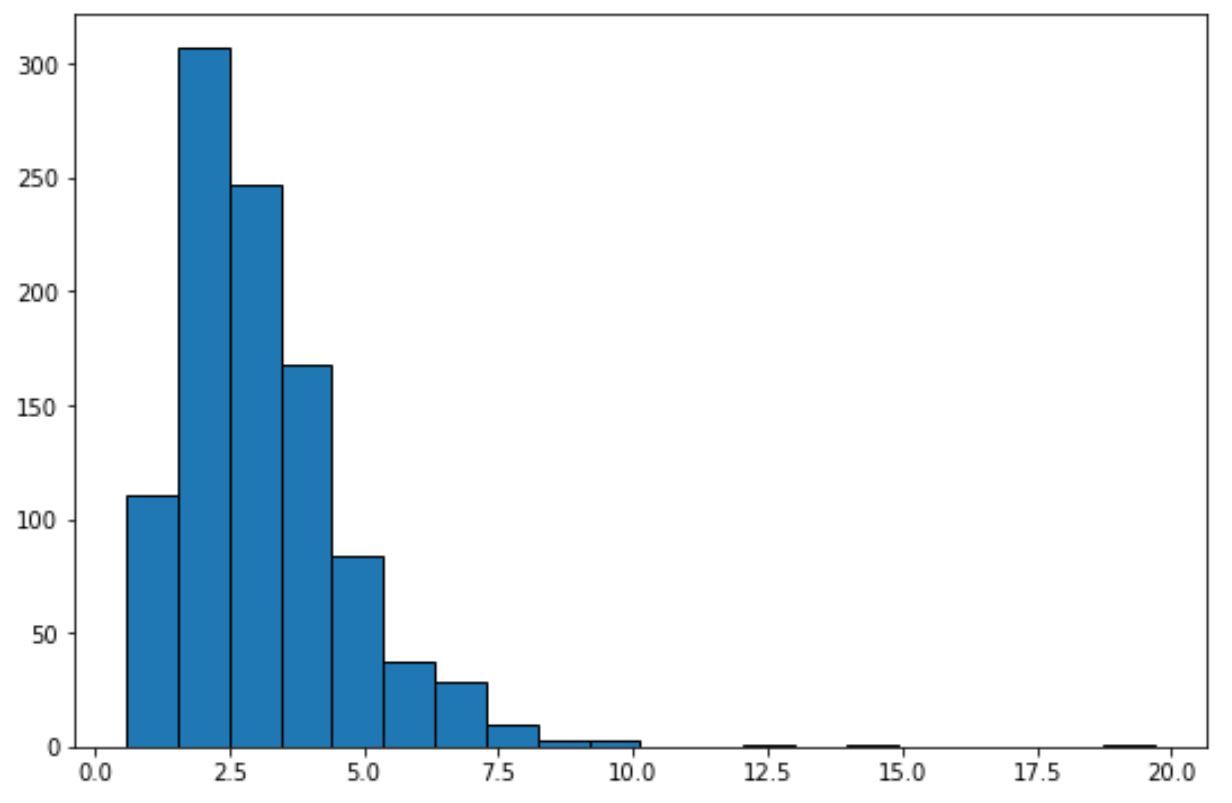
Alleen al door naar dit histogram te kijken, kunnen we zien dat de dataset geen “klokvorm” vertoont en niet normaal verdeeld is.

Methode 2: Maak een QQ-plot

De volgende code laat zien hoe u een QQ-plot maakt voor een gegevensset die een lognormale verdeling volgt:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

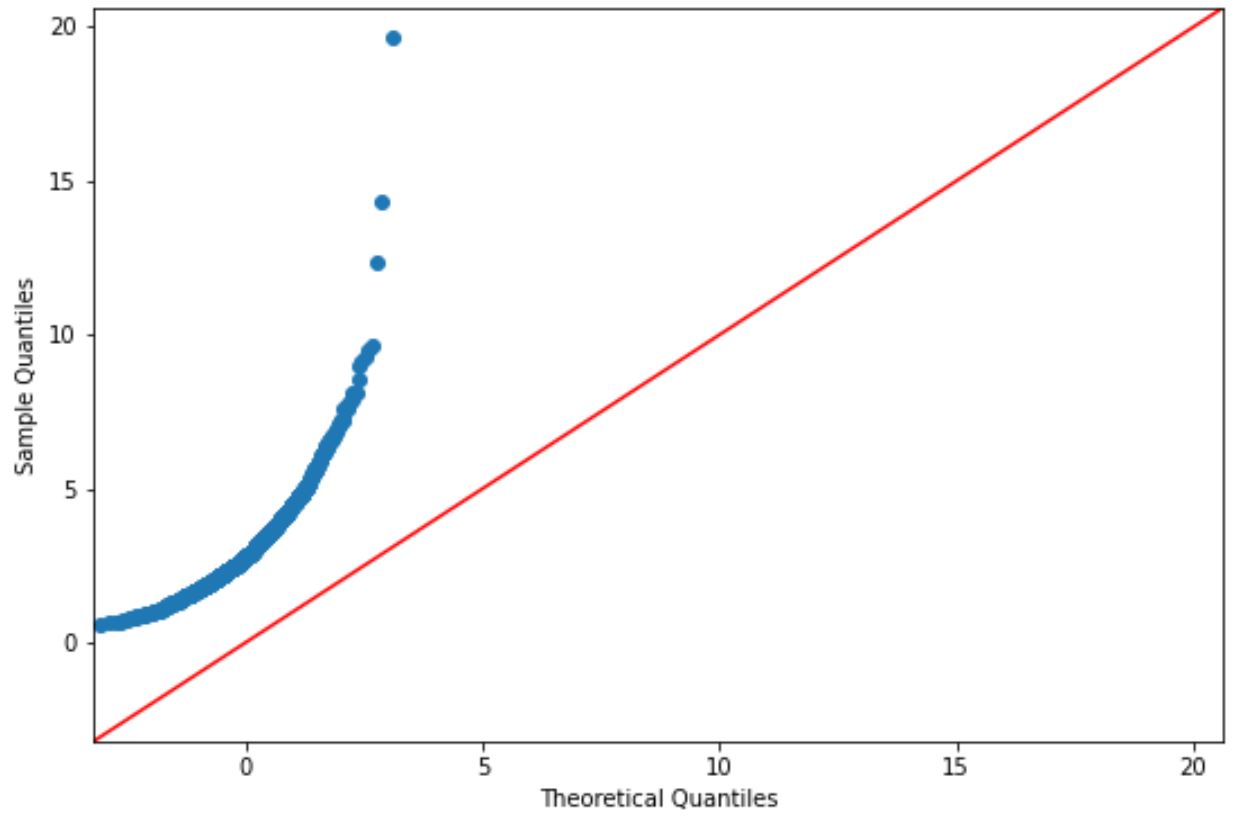
Als de plotpunten ongeveer langs een rechte diagonale lijn liggen, gaan we er doorgaans van uit dat een dataset normaal verdeeld is.

De punten in deze grafiek komen echter duidelijk niet overeen met de rode lijn, dus we kunnen niet aannemen dat deze gegevensset normaal verdeeld is.

Dit zou logisch moeten zijn, aangezien we de gegevens hebben gegenereerd met behulp van een lognormale verdelingsfunctie.

Methode 3: Voer een Shapiro-Wilk-test uit

De volgende code laat zien hoe u een Shapiro-Wilk uitvoert voor een gegevensset die een log-normale verdeling volgt:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Uit het resultaat kunnen we zien dat de teststatistiek 0,857 is en de overeenkomstige p-waarde 3,88e-29 (extreem dicht bij nul).

Omdat de p-waarde kleiner is dan 0,05, verwerpen we de nulhypothese van de Shapiro-Wilk-test.

Dit betekent dat we voldoende bewijs hebben om te zeggen dat de steekproefgegevens niet uit een normale verdeling komen.

Methode 4: Voer een Kolmogorov-Smirnov-test uit

De volgende code laat zien hoe u een Kolmogorov-Smirnov-test uitvoert voor een gegevensset die een lognormale verdeling volgt:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Uit het resultaat kunnen we zien dat de teststatistiek 0,841 is en de overeenkomstige p-waarde 0,0 .

Omdat de p-waarde kleiner is dan 0,05, verwerpen we de nulhypothese van de Kolmogorov-Smirnov-test.

Dit betekent dat we voldoende bewijs hebben om te zeggen dat de steekproefgegevens niet uit een normale verdeling komen.

Hoe om te gaan met niet-normale gegevens

Als een bepaalde dataset niet normaal verdeeld is , kunnen we vaak een van de volgende transformaties uitvoeren om deze normaler verdeeld te maken:

1. Logtransformatie: transformeer x-waarden naar log(x) .

2. Vierkantsworteltransformatie: Transformeer de waarden van x naar √x .

3. Derdemachtsworteltransformatie: transformeer de waarden van x naar x ^1/3 .

Door deze transformaties uit te voeren, wordt de dataset doorgaans normaler verdeeld.

Lees deze tutorial om te zien hoe u deze transformaties in Python uitvoert.