Hoe u een restplot maakt in python

Een residuele plot is een type plot dat gepaste waarden weergeeft tegen de residuen van een regressiemodel .

Dit type plot wordt vaak gebruikt om te evalueren of een lineair regressiemodel al dan niet geschikt is voor een bepaalde dataset en om residuen te controleren op heteroskedasticiteit .

In deze tutorial wordt uitgelegd hoe u een residuele plot maakt voor een lineair regressiemodel in Python.

Voorbeeld: restplot in Python

Voor dit voorbeeld gebruiken we een dataset die de kenmerken van 10 basketbalspelers beschrijft:

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

Residuele plot voor eenvoudige lineaire regressie

Stel dat we een eenvoudig lineair regressiemodel passen met punten als voorspellende variabele en cijfer als responsvariabele:

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

We kunnen een residuele of gepaste plot maken met behulp van de plot_regress_exog() functie uit de statsmodels bibliotheek:

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

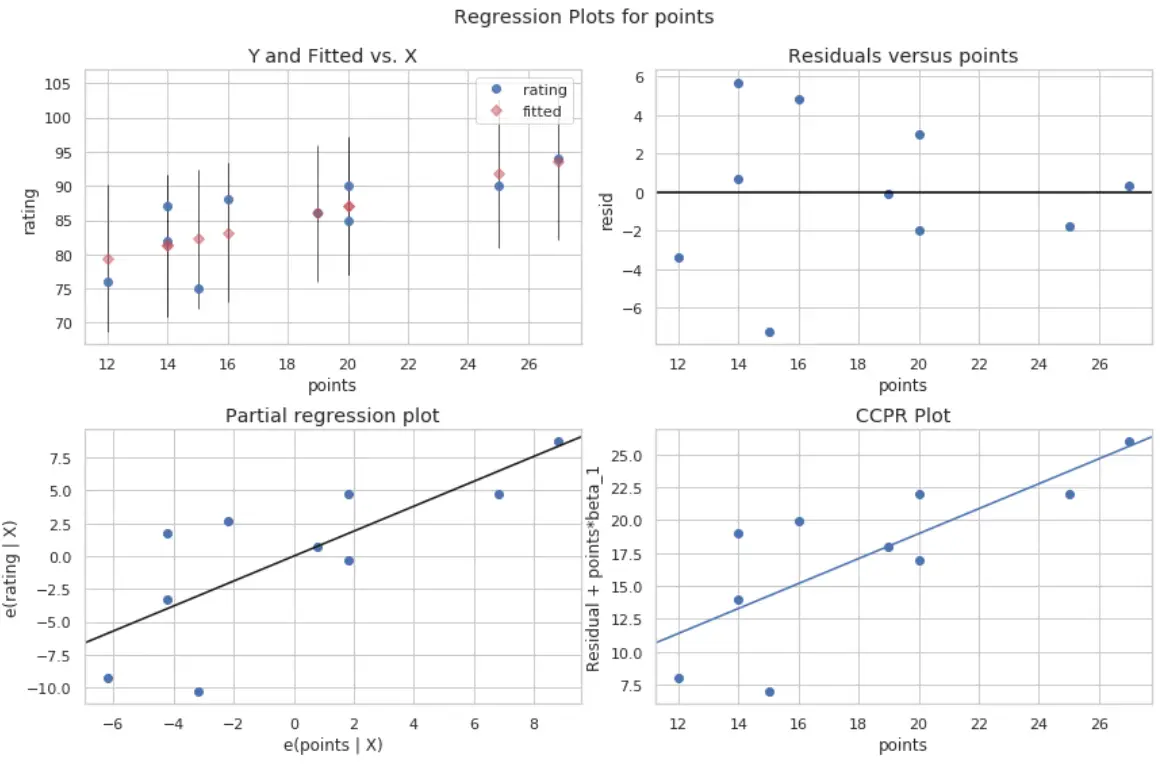
Er worden vier percelen geproduceerd. De grafiek in de rechterbovenhoek is de restgrafiek versus de aangepaste grafiek. De x-as in deze grafiek toont de werkelijke waarden van de punten van de voorspellende variabele en de y-as toont het residu voor die waarde.

Omdat de residuen willekeurig rond nul verspreid lijken te zijn, geeft dit aan dat heteroscedasticiteit geen probleem is met de voorspellende variabele.

Residuele plots voor meervoudige lineaire regressie

Stel dat we in plaats daarvan een meervoudig lineair regressiemodel toepassen met assists en rebounds als voorspellende variabele en rating als responsvariabele:

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

Wederom kunnen we voor elk van de individuele voorspellers een residuele versus voorspellende plot maken met behulp van de plot_regress_exog() functie uit de statsmodels-bibliotheek.

Dit is bijvoorbeeld hoe de rest/voorspellerplot eruit ziet voor hulp bij voorspellende variabelen:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

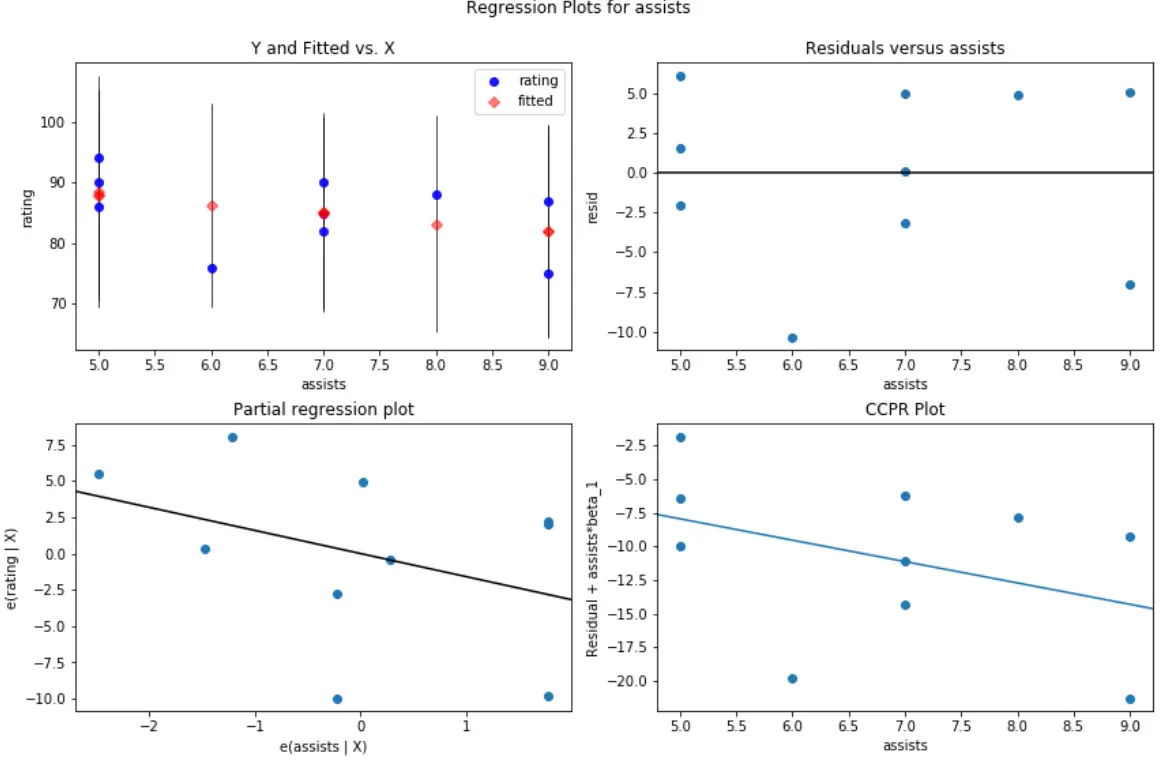
En dit is hoe de rest/voorspellerplot eruit ziet voor de bounces van de voorspellende variabele:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

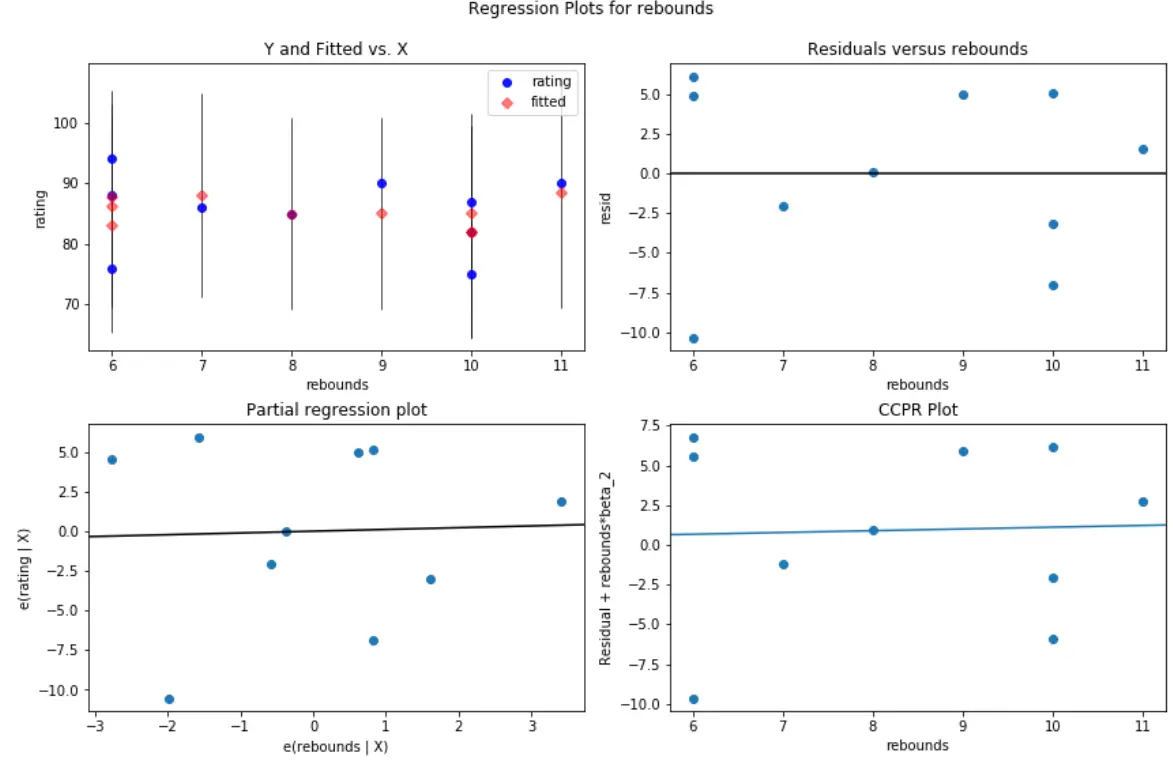
In beide grafieken lijken de residuen willekeurig rond nul verspreid te zijn, wat aangeeft dat heteroskedasticiteit geen probleem is met een van de voorspellende variabelen in het model.