Quasi-standaarddeviatie

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat quasi-standaarddeviatie in statistieken is en hoe deze wordt berekend. Zo vind je de quasi-standaardafwijkingsformule, een opgeloste oefening en bovendien een online calculator om de quasi-standaardafwijking van elke dataset te berekenen.

Wat is quasi-standaardafwijking?

In de statistiek is de quasi-standaardafwijking een maatstaf voor de spreiding die de variabiliteit van de steekproef aangeeft. Concreet is de quasi-standaardafwijking gelijk aan de vierkantswortel van de som van de kwadraten van de afwijkingen gedeeld door het totale aantal gegevenspunten min één.

Het symbool voor de quasi-standaarddeviatie is σ _n-1 os _n-1 .

Quasi-standaardafwijking wordt ook wel quasi-standaardafwijking genoemd, en wordt ook wel steekproefstandaardafwijking genoemd, omdat deze meestal wordt berekend met behulp van waarden uit een statistische steekproef. Hieronder zullen we in detail ingaan op het verschil tussen quasi-standaardafwijking en standaardafwijking.

Quasi-standaardafwijkingsformule

De quasi-standaardafwijking is gelijk aan de vierkantswortel van de som van de kwadraten van de afwijkingen van de gegevensreeks gedeeld door het totale aantal waarnemingen min één. Daarom is de formule voor het berekenen van de quasi-standaardafwijking :

formule voor quasi-standaardafwijking (of quasi-standaardafwijking).

Goud:

$\sigma_{n-1}$

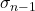
Dit is de quasi-standaarddeviatie.
$x_i$

is de gegevenswaarde

$i$

.
$n$

is het totale aantal gegevens.
$\overline{x}$

is het gemiddelde van de dataset.

👉 U kunt de onderstaande rekenmachine gebruiken om de quasi-standaardafwijking voor elke dataset te berekenen.

Voorbeeld van het berekenen van quasi-standaardafwijking

Gezien de definitie van quasi-standaardafwijking, ziet u hieronder een eenvoudig voorbeeld van hoe u de quasi-standaardafwijking van een dataset kunt berekenen.

Het budget van een bedrijf voor zijn onderzoeks- en ontwikkelingsafdeling is zeer volatiel, omdat het afhangt van de economische winst die het bedrijf het voorgaande jaar heeft behaald. Het budget voor deze afdeling over de afgelopen vijf jaar was dus: 3, 6, 2, 9, 4 miljoen euro. Bereken de quasi-standaarddeviatie van deze gegevensreeks.

Het eerste dat we moeten doen om de quasi-standaardafwijking te bepalen, is het rekenkundig gemiddelde van de steekproef berekenen. Om dit te doen, tellen we alle gegevens bij elkaar op en delen we deze door het totale aantal waarnemingen, namelijk vijf:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Vervolgens passen we de quasi-standaardafwijkingsformule toe:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

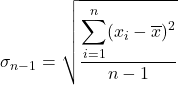
We vervangen de gegevens in de formule:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

En tenslotte berekenen we de quasi-standaardafwijking:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

Kortom, de quasi-standaardafwijking van de gegevenssteekproef is 2,77 miljoen.

➤ Zie: Quasivariantie

Quasi-standaardafwijkingscalculator

Sluit een statistische gegevensset aan op de onderstaande online calculator om de quasi-standaardafwijking ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Quasi-standaardafwijking en standaardafwijking

Ten slotte zullen we zien wat het verschil is tussen quasi-standaarddeviatie en standaarddeviatie, aangezien het twee verschillende statistische metingen zijn die een zeer vergelijkbare naam hebben en op een zeer vergelijkbare manier worden berekend.

Het verschil tussen de quasi-standaardafwijking en de standaardafwijking is de noemer van de formule. Om de quasi-standaardafwijking te berekenen, deelt u door n-1, maar de standaardafwijking wordt berekend door te delen door n.

Daarom zijn quasi-standaardafwijking en standaardafwijking wiskundig gerelateerd, aangezien quasi-standaardafwijking gelijk is aan standaardafwijking maal de vierkantswortel van n (totaal aantal gegevenspunten) over n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

Uit de voorgaande vergelijking kunnen we afleiden dat voor dezelfde set gegevens de waarde van de quasi-standaardafwijking altijd groter zal zijn dan de waarde van de standaardafwijking.

Bovendien wordt de quasi-standaardafwijkingsformule vaak gebruikt om de standaardafwijking van een steekproef te berekenen, omdat deze vertekening elimineert. De quasi-standaarddeviatie is daarom een goede schatter van de populatiestandaarddeviatie. Dit is de reden waarom het bij het maken van een statistische gevolgtrekking uit een steekproef heel gebruikelijk is om te zeggen dat de standaardafwijking wordt berekend, terwijl het in werkelijkheid de quasi-standaardafwijking is die wordt berekend.

➤ Zie: Eigenschappen van standaarddeviatie

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder