R versus r-square: wat is het verschil?

Twee termen die leerlingen vaak verwarren in de statistiek zijn R en R-kwadraat , vaak geschreven als ^R2 .

In de context van een eenvoudige lineaire regressie :

• A: De correlatie tussen de voorspellende variabele, x, en de responsvariabele, y.
• R ² : Aandeel van de variantie in de responsvariabele dat kan worden verklaard door de voorspellende variabele in het regressiemodel.

En in de context van een meervoudige lineaire regressie :

• A: De correlatie tussen de waargenomen waarden van de responsvariabele en de voorspelde waarden van de responsvariabele die door het model worden gemaakt.
• R ² : Aandeel van de variantie van de responsvariabele dat kan worden verklaard door de voorspellende variabelen van het regressiemodel.

Merk op dat de waarde van R ² tussen 0 en 1 ligt. Hoe dichter de waarde bij 1 ligt, hoe sterker de relatie tussen de voorspellende variabele(n) en de responsvariabele.

De volgende voorbeelden laten zien hoe u R- en R-kwadraatwaarden kunt interpreteren in eenvoudige lineaire regressie- en meervoudige lineaire regressiemodellen.

Voorbeeld 1: Eenvoudige lineaire regressie

Stel dat we de volgende dataset hebben die de gestudeerde uren en examenscores van 12 studenten in een bepaalde wiskundecursus laat zien:

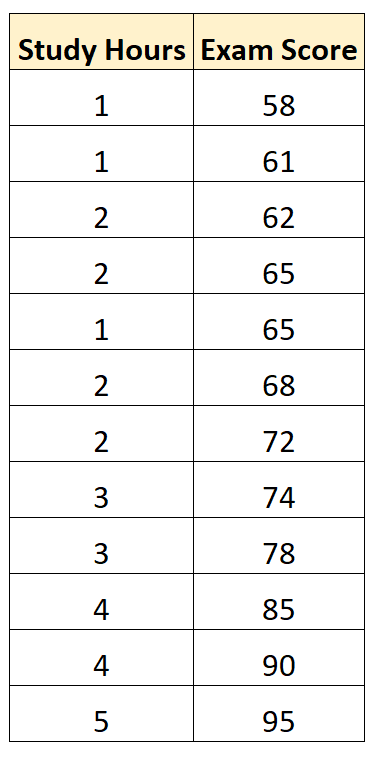
Met behulp van statistische software (zoals Excel, R, Python, SPSS, etc.) kunnen we een eenvoudig lineair regressiemodel opstellen met ’studie-uren‘ als voorspellende variabele en ‚examencijfer‘ alsresponsvariabele .

We kunnen de volgende uitvoer voor dit model vinden:

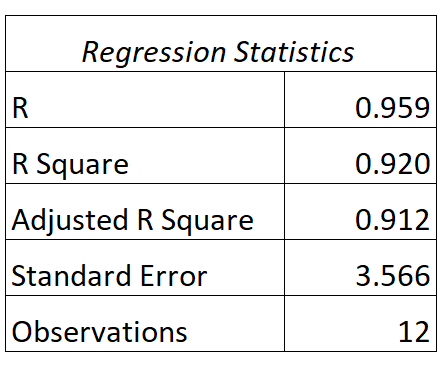
Zo interpreteert u de R- en R-kwadraatwaarden van dit model:

• A: De correlatie tussen het aantal gestudeerde uren en de examenscore is 0,959 .
• ^R2 : De R-kwadraat voor dit regressiemodel is 0,920 . Dit leert ons dat 92,0% van de variatie in examenscores kan worden verklaard door het aantal gestudeerde uren.

Merk ook op dat de R ² -waarde eenvoudigweg gelijk is aan de R-waarde, in het kwadraat:

^R2 = R * R = 0,959 * 0,959 = 0,920

Voorbeeld 2: Meervoudige lineaire regressie

Stel dat we de volgende dataset hebben die het aantal gestudeerde uren, het huidige cijfer van de leerling en het examencijfer laat zien dat twaalf leerlingen voor een bepaalde wiskundecursus hebben behaald:

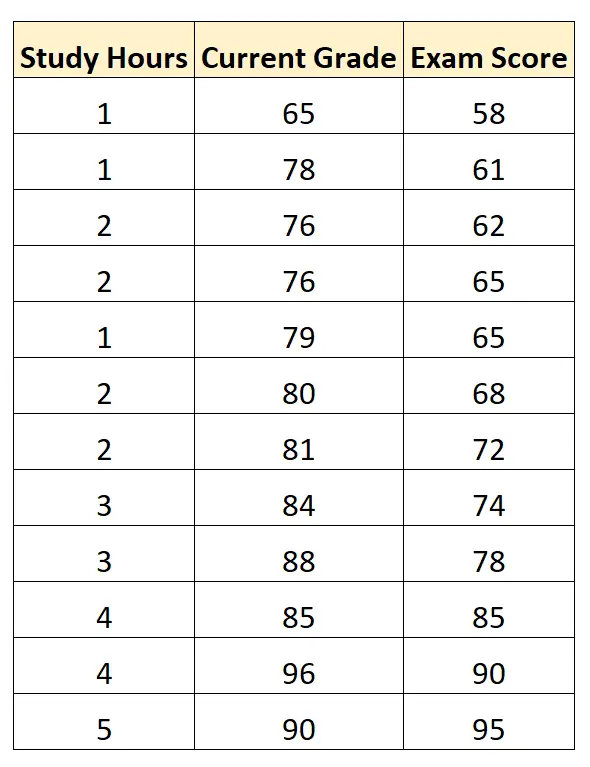
Met behulp van statistische software kunnen we een meervoudig lineair regressiemodel opstellen met ‘studie-uren’ en ‘huidig cijfer’ als voorspellende variabelen en ‘examencijfer’ als responsvariabele.

We kunnen de volgende uitvoer voor dit model vinden:

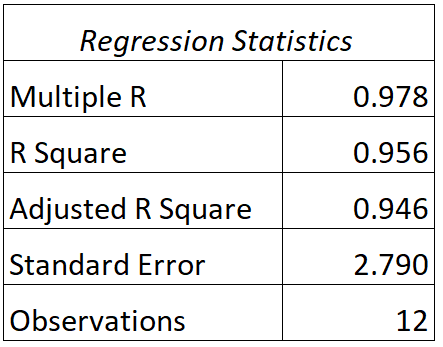
Zo interpreteert u de R- en R-kwadraatwaarden van dit model:

• A: De correlatie tussen de werkelijke testscores en de voorspelde testscores van het model is 0,978 .
• ^R2 : De R-kwadraat voor dit regressiemodel is 0,956 . Dit vertelt ons dat 95,6% van de variatie in examenscores kan worden verklaard door het aantal gestudeerde uren en het huidige cijfer van de student in de klas.

Merk ook op dat de R ² -waarde eenvoudigweg gelijk is aan de R-waarde, in het kwadraat:

^R2 = R * R = 0,978 * 0,978 = 0,956

Aanvullende bronnen

Wat is een goede R-kwadraatwaarde?
Een vriendelijke gids voor de som van de kwadraten: SST, SSR, SSE