Een inleiding tot de rayleigh-distributie

De Rayleigh-verdeling is een continue kansverdeling die wordt gebruikt om willekeurige variabelen te modelleren die alleen waarden kunnen aannemen die gelijk zijn aan of groter dan nul.

Het heeft de volgende waarschijnlijkheidsdichtheidsfunctie:

f(x; σ) = (x/σ ² )e ^{-x 2 /(2σ 2 )}

waarbij σ de schaalparameter van de verdeling is.

Eigenschappen van de Rayleigh-verdeling

De Rayleigh-verdeling heeft de volgende eigenschappen:

• Gemiddeld: σ√ π/2
• Afwijking: ((4-π)/2)σ ²
• Modus: σ

Omdat π een bekende numerieke waarde heeft, kunnen we de eigenschappen als volgt vereenvoudigen:

• Gemiddeld: 1,253σ
• Afwijking: 0,429σ ²
• Modus: σ

Visualisatie van de Rayleigh-verdeling

De volgende grafiek toont de vorm van de Rayleigh-verdeling, aangezien er verschillende waarden voor de schaalparameter nodig zijn:

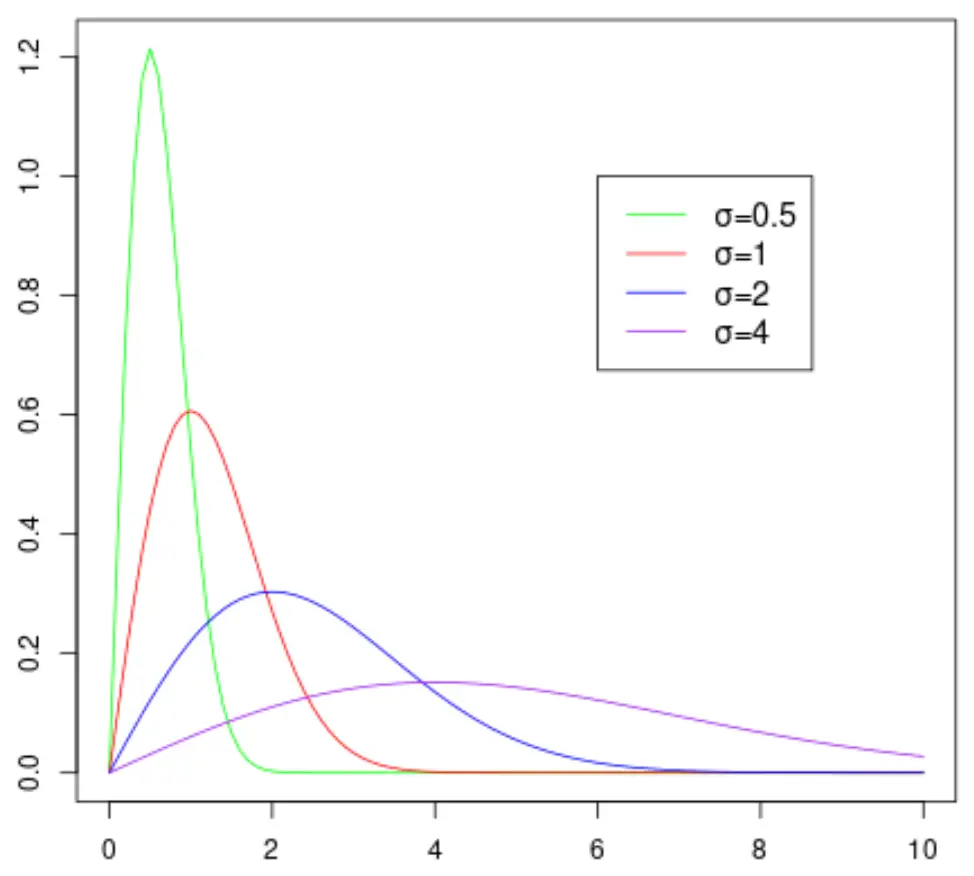
Merk op dat hoe groter de waarde van de schaalparameter σ, hoe breder de verdeling wordt.

Bonus: voor degenen die nieuwsgierig zijn, hebben we de volgende R-code gebruikt om de bovenstaande grafiek te genereren:

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

Relatie met andere distributies

De Rayleigh-verdeling heeft de volgende relatie met andere kansverdelingen:

1. Wanneer de schaalparameter (σ) gelijk is aan 1, is de Rayleigh-verdeling gelijk aan een Chi-kwadraatverdeling met 2 vrijheidsgraden.

2. De Rayleigh-verdeling is een speciaal geval van de Weibull-verdeling met een vormparameter k = 2.

3. De Rayleigh-verdeling met schaalparameter σ is gelijk aan de Rijstverdeling met Rijst(0, σ).

Toepassingen

In de praktijk wordt de Rayleigh-verdeling in verschillende toepassingen gebruikt, waaronder:

1. De Rayleigh-verdeling wordt gebruikt om het gedrag van golven in de oceaan te modelleren, inclusief de tijd die golven nodig hebben om hun top te bereiken en de maximale hoogte die de golven bereiken.

2. De Rayleigh-verdeling wordt gebruikt om het gedrag van achtergrondgegevens in magnetische resonantiebeeldvorming, beter bekend als MRI, te modelleren.

3. De Rayleigh-verdeling wordt op het gebied van voeding gebruikt om de relatie tussen nutriëntenniveaus en voedingsrespons bij mens en dier te modelleren.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over andere verdelingen in statistieken:

Een inleiding tot de normale verdeling
Een inleiding tot de binominale verdeling
Een inleiding tot de Poisson-verdeling