Regressie lijn

Von Dr.benjamin anderson August 2, 2023 Statistieken Keine Kommentare

Dit artikel legt uit wat regressielijn is in statistieken. U vindt dus hoe u de regressielijn tussen twee variabelen kunt berekenen, een opgeloste oefening en bovendien een online rekenmachine om de regressielijn voor elk gegevensmonster te berekenen.

Wat is de regressielijn?

In de statistiek is de regressielijn de lijn die wordt verkregen uit een eenvoudig lineair regressiemodel . Preciezer gezegd: de regressielijn is de lijn die het beste past bij een spreidingsdiagram en daarom het beste een reeks statistische gegevens beschrijft.

De regressielijnvergelijking relateert dus wiskundig de onafhankelijke variabele X en de afhankelijke variabele Y van een reeks gegevens. Hoewel de regressielijn doorgaans niet in staat is de waarde van elke waarneming nauwkeurig te bepalen, kan deze wel een benadering van de waarde ervan opleveren.

Zoals je in de vorige grafiek kunt zien, helpt de regressielijn ons de trend van een dataset te zien en welk type relatie er bestaat tussen de onafhankelijke variabele en de afhankelijke variabele. Hieronder zullen we kijken naar toepassingen van de regressielijn.

Regressielijnformule

Nu we de definitie van de regressielijn kennen, gaan we kijken hoe we de vergelijking van de lijn van een lineair regressiemodel kunnen berekenen.

Zoals elke lijn bestaat de vergelijking van de regressielijn uit een constante (b ₀ ) en een helling (b ₁ ):

$y=b_0+b_1x$

De formules voor het berekenen van de coëfficiënten van de lineaire regressielijn zijn dus als volgt:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

Goud:

$b_0$

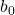
is de constante van de regressielijn.
$b_1$

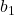
is de helling van de regressielijn.
$x_i$

is de waarde van de onafhankelijke variabele X van gegevens i.
$y_i$

is de waarde van de afhankelijke variabele Y van gegevens i.
$\overline{x}$

is het gemiddelde van de waarden van de onafhankelijke variabele
$\overline{y}$

is het gemiddelde van de waarden van de afhankelijke variabele Y.

👉 U kunt de onderstaande rekenmachine gebruiken om de regressielijn voor elke gegevensset te berekenen.

Concreet voorbeeld van de regressielijn

Om het concept van een regressielijn verder te verkennen, vindt u hieronder een uitgewerkt voorbeeld van hoe u een regressielijn kunt maken.

Na het afleggen van een statistiektentamen is aan vijf studenten gevraagd hoeveel uren studie ze aan het tentamen hebben besteed, de gegevens staan in onderstaande tabel. Bereken de regressielijn uit de verzamelde statistische gegevens om de studie-uren lineair te relateren aan het behaalde cijfer. Bepaal vervolgens welk cijfer een leerling die 8 uur heeft gestudeerd krijgt.

Om de regressielijn voor de voorbeeldgegevens te vinden, moeten we de coëfficiënten b ₀ en b ₁ van de vergelijking bepalen en om dit te doen moeten we de formules gebruiken die we in het bovenstaande gedeelte hebben gezien.

Om de formules voor de lineaire regressielijn toe te passen, moeten we echter eerst het gemiddelde van de onafhankelijke variabele en het gemiddelde van de afhankelijke variabele berekenen:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Nu we de gemiddelden van de variabelen kennen, berekenen we de coëfficiënt b ₁ van het model met behulp van de bijbehorende formule:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Ten slotte berekenen we de coëfficiënt b ₀ van het model met behulp van de bijbehorende formule:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Kort gezegd is de vergelijking van de lineaire regressielijn van het probleem als volgt:

$y=2,0294+0,4412x$

Hieronder ziet u de grafische weergave van de voorbeeldgegevens, evenals de rechte lijn van het eenvoudige lineaire regressiemodel:

Zodra we de regressielijn hebben berekend, kunt u, om het cijfer te voorspellen dat een student die 8 uur heeft gestudeerd, deze waarde zal behalen eenvoudigweg deze waarde vervangen door de vergelijking van de verkregen regressielijn:

$y=2,0294+0,4412\cdot 8=5,56$

Volgens het uitgevoerde lineaire regressiemodel krijgt een student dus een score van 5,56 op het examen als hij acht uur heeft gestudeerd.

Waar wordt een regressielijn voor gebruikt?

Hoofdzakelijk heeft de regressielijn twee toepassingen: de regressielijn wordt gebruikt om te bepalen welk type relatie er bestaat tussen twee variabelen en aan de andere kant kunt u met de regressielijn ook een voorspelling doen over de waarde van een nieuwe waarneming.

De helling van de regressielijn vertelt ons hoe de correlatie tussen de onafhankelijke variabele en de afhankelijke variabele is. Als de helling positief is, betekent dit dat de afhankelijke variabele direct evenredig is met de onafhankelijke variabele, terwijl als de helling negatief is, dit impliceert dat de variabelen omgekeerd evenredig zijn. Als de hellingscoëfficiënt ten slotte heel dicht bij nul ligt, betekent dit dat de correlatie tussen de twee variabelen erg zwak is.

Als de vergelijking van de regressielijn bekend is, kan bovendien de waarde van de afhankelijke variabele worden voorspeld voor een nieuwe waarde van de onafhankelijke variabele, zoals we in het bovenstaande voorbeeld hebben gedaan. Dus hoe beter de regressielijn wordt aangepast, hoe beter de voorspellingen die deze zal doen.

Regressielijncalculator

Voer een voorbeeld van gegevens in de volgende rekenmachine in om de regressielijn tussen de twee variabelen te berekenen. U moet de gegevensparen scheiden, zodat in het eerste vak alleen de waarden van de onafhankelijke variabele X staan en in het tweede vak alleen de waarden van de afhankelijke variabele Y.

Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder