Inleiding tot ridge-regressie

Bij gewone meervoudige lineaire regressie gebruiken we een reeks p- voorspellingsvariabelen en een responsvariabele om in een model van de vorm te passen:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Goud:

• Y : De responsvariabele
• _Xj : de j ^-de voorspellende variabele
• _βj : Het gemiddelde effect op Y van een toename van één eenheid in _Xj , waarbij alle andere voorspellers vast blijven
• ε : De foutterm

De waarden van β ₀ , β ₁ , B ₂ , …, β _p worden gekozen met behulp van de kleinste kwadratenmethode , die de som van de kwadraten van de residuen (RSS) minimaliseert:

RSS = Σ(y _i – ŷ _i ) ²

Goud:

• Σ : Een Grieks symbool dat som betekent
• y _i : de werkelijke responswaarde voor de ^i-de waarneming
• ŷ _i : De voorspelde responswaarde op basis van het meervoudige lineaire regressiemodel

Wanneer voorspellende variabelen echter sterk gecorreleerd zijn, kan multicollineariteit een probleem worden. Dit kan schattingen van modelcoëfficiënten onbetrouwbaar maken en een hoge variantie vertonen.

Eén manier om dit probleem te omzeilen zonder bepaalde voorspellende variabelen volledig uit het model te verwijderen, is door een methode te gebruiken die bekend staat als ridge regressie , die in plaats daarvan het volgende probeert te minimaliseren:

RSS + λΣβ _j ²

waarbij j van 1 naar p gaat en λ ≥ 0.

Deze tweede term in de vergelijking staat bekend als de opnameboete .

Wanneer λ = 0 heeft deze strafterm geen effect en levert nokregressie dezelfde coëfficiëntschattingen op als de kleinste kwadraten. Naarmate λ het oneindige nadert, wordt de krimp echter steeds invloedrijker en naderen de schattingen van de piekregressiecoëfficiënt nul.

Over het algemeen zullen de minst invloedrijke voorspellende variabelen in het model het snelst naar nul dalen.

Waarom Ridge-regressie gebruiken?

Het voordeel van Ridge-regressie ten opzichte van regressie met de kleinste kwadraten is de afweging tussen bias en variantie .

Bedenk dat Mean Square Error (MSE) een metriek is die we kunnen gebruiken om de nauwkeurigheid van een bepaald model te meten en die als volgt wordt berekend:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Variantie + Bias ² + Onherleidbare fout

Het basisidee van Ridge-regressie is om een kleine vertekening te introduceren, zodat de variantie aanzienlijk kan worden verminderd, wat leidt tot een lagere algehele MSE.

Om dit te illustreren, bekijken we de volgende grafiek:

Merk op dat naarmate λ toeneemt, de variantie aanzienlijk afneemt met een zeer kleine toename van de bias. Vanaf een bepaald punt neemt de variantie echter minder snel af en leidt de afname van de coëfficiënten tot een significante onderschatting ervan, wat leidt tot een scherpe toename van de bias.

We kunnen uit de grafiek zien dat de MSE van de test het laagst is als we een waarde voor λ kiezen die een optimale afweging tussen vertekening en variantie oplevert.

Wanneer λ = 0 heeft de strafterm in de nokregressie geen effect en levert daarom dezelfde coëfficiëntschattingen op als de kleinste kwadraten. Door λ echter tot een bepaald punt te verhogen, kunnen we de algehele MSE van de test verminderen.

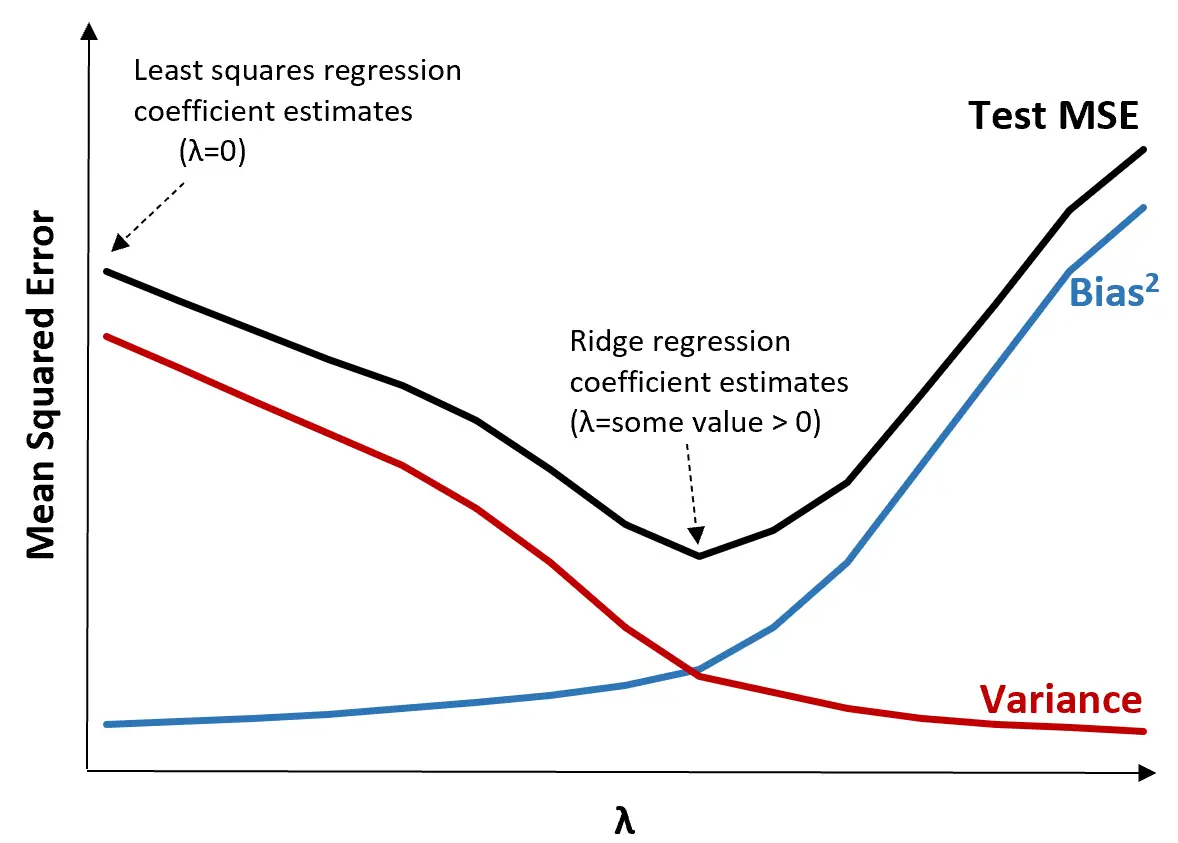
Dit betekent dat modelaanpassing door middel van ridge-regressie kleinere testfouten zal opleveren dan modelaanpassing door middel van kleinste-kwadratenregressie.

Stappen om Ridge-regressie in de praktijk uit te voeren

De volgende stappen kunnen worden gebruikt om nokregressie uit te voeren:

Stap 1: Bereken de correlatiematrix en VIF-waarden voor de voorspellende variabelen.

Eerst moeten we een correlatiematrix maken en de VIF-waarden (variantie-inflatiefactor) voor elke voorspellende variabele berekenen.

Als we een sterke correlatie detecteren tussen de voorspellende variabelen en hoge VIF-waarden (sommige teksten definiëren een „hoge“ VIF-waarde als 5, terwijl andere 10 gebruiken), dan is randregressie waarschijnlijk geschikt.

Als er echter geen multicollineariteit in de gegevens aanwezig is, is het misschien niet nodig om ridge-regressie uit te voeren. In plaats daarvan kunnen we gewone regressie met de kleinste kwadraten uitvoeren.

Stap 2: Standaardiseer elke voorspellende variabele.

Voordat we ridge-regressie uitvoeren, moeten we de gegevens zo schalen dat elke voorspellende variabele een gemiddelde van 0 en een standaarddeviatie van 1 heeft. Dit zorgt ervoor dat geen enkele voorspellende variabele een buitensporige invloed heeft bij het uitvoeren van een ridge-regressie.

Stap 3: Pas het nokregressiemodel aan en kies een waarde voor λ.

Er is geen exacte formule die we kunnen gebruiken om te bepalen welke waarde we voor λ moeten gebruiken. In de praktijk zijn er twee veel voorkomende manieren om λ te kiezen:

(1) Maak een Ridge-traceerplot. Dit is een grafiek die de waarden van de coëfficiëntschattingen visualiseert naarmate λ toeneemt richting oneindig. Meestal kiezen we λ als de waarde waarbij de meeste coëfficiëntschattingen beginnen te stabiliseren.

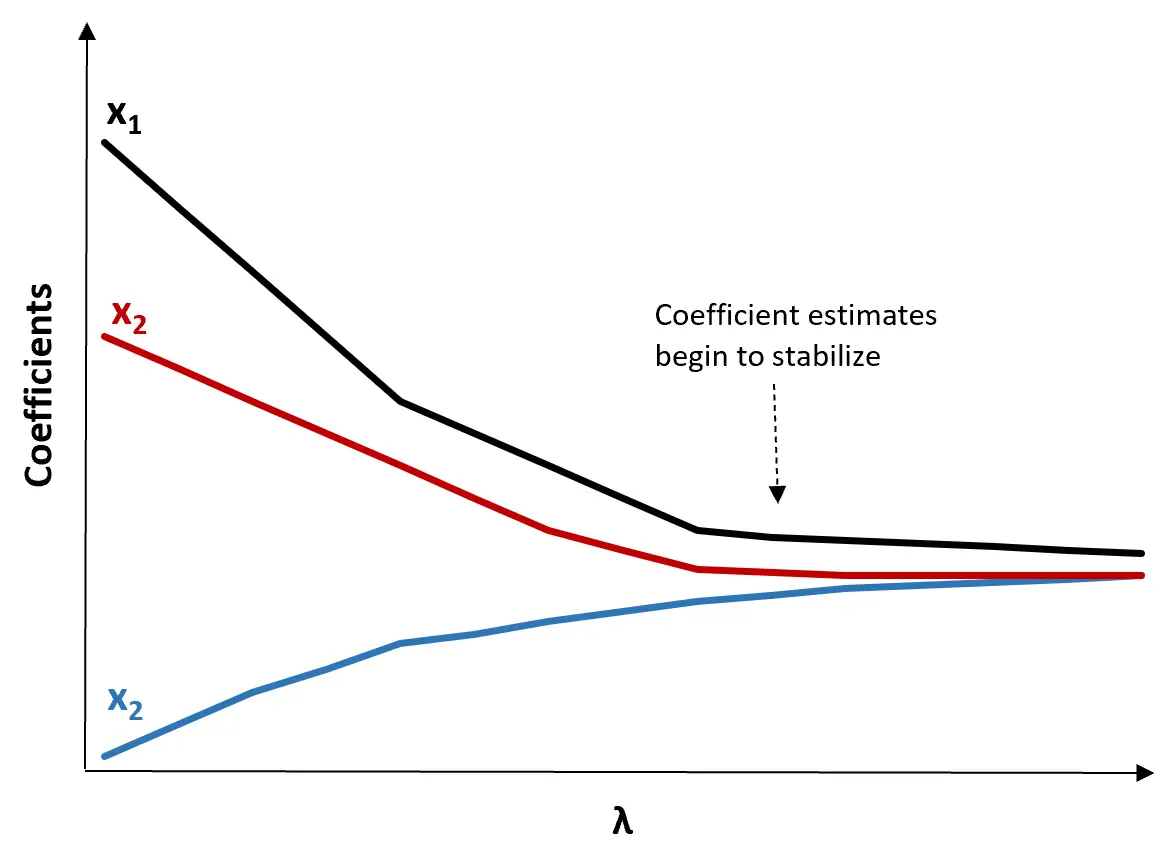
(2) Bereken de MSE-test voor elke waarde van λ.

Een andere manier om λ te kiezen is door eenvoudigweg de test-MSE van elk model met verschillende waarden van λ te berekenen en λ te kiezen als de waarde die de laagste test-MSE oplevert.

Voor- en nadelen van Ridge-regressie

Het grootste voordeel van Ridge-regressie is het vermogen om een lagere testgemiddelde kwadratenfout (MSE) te produceren dan de kleinste kwadraten wanneer multicollineariteit aanwezig is.

Het grootste nadeel van Ridge-regressie is echter het onvermogen om variabelen te selecteren, aangezien alle voorspellende variabelen in het uiteindelijke model worden opgenomen. Omdat sommige voorspellers zeer dicht bij nul zullen worden teruggebracht, kan dit het moeilijk maken om de modelresultaten te interpreteren.

In de praktijk heeft Ridge-regressie het potentieel om een model te produceren dat betere voorspellingen kan doen vergeleken met een kleinste-kwadratenmodel, maar het is vaak moeilijker om de resultaten van het model te interpreteren.

Afhankelijk van of modelinterpretatie of voorspellingsnauwkeurigheid belangrijker voor u is, kunt u ervoor kiezen om in verschillende scenario’s gewone kleinste kwadraten of nokregressie te gebruiken.

Ridge-regressie in R & Python

In de volgende tutorials wordt uitgelegd hoe u ridge-regressie uitvoert in R en Python, de twee meest gebruikte talen voor het aanpassen van ridge-regressiemodellen:

Ridge-regressie in R (stap voor stap)
Ridge-regressie in Python (stap voor stap)