Regressie door de oorsprong: definitie en voorbeeld

Eenvoudige lineaire regressie is een methode die kan worden gebruikt om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te kwantificeren.

Een eenvoudig lineair regressiemodel heeft de volgende vorm:

y = β ₀ + β ₁ x

Goud:

• y : De waarde van de responsvariabele
• β ₀ : De waarde van de responsvariabele wanneer x = 0 (de “intercept”-term genoemd)
• β ₁ : De gemiddelde toename van de responsvariabele geassocieerd met een toename van één eenheid in x
• x : De waarde van de voorspellende variabele

Een aangepaste versie van dit model staat bekend als regressie door de oorsprong , waardoor y gelijk is aan 0 wanneer x gelijk is aan 0.

Dit type model heeft de volgende vorm:

y = _β1x

Merk op dat de intercept-term volledig uit het model is verwijderd.

Dit model wordt soms gebruikt als onderzoekers weten dat de responsvariabele nul moet zijn als de voorspellende variabele nul is.

In de echte wereld wordt dit type model het vaakst gebruikt in bosbouw- of ecologische studies .

Onderzoekers kunnen bijvoorbeeld de boomomtrek gebruiken om de boomhoogte te voorspellen. Als een bepaalde boom een omtrek van nul heeft, moet deze ook een hoogte van nul hebben.

Dus als een regressiemodel op deze gegevens wordt toegepast, zou het niet logisch zijn als de oorspronkelijke term niet nul zou zijn.

Het volgende voorbeeld laat het verschil zien tussen het aanpassen van een gewoon eenvoudig lineair regressiemodel en een model dat regressie via de oorsprong implementeert.

Voorbeeld: regressie via de oorsprong

Stel dat een bioloog een regressiemodel wil passen met behulp van de boomomtrek om de boomhoogte te voorspellen. Ze gaat eropuit en verzamelt de volgende metingen voor een steekproef van 15 bomen:

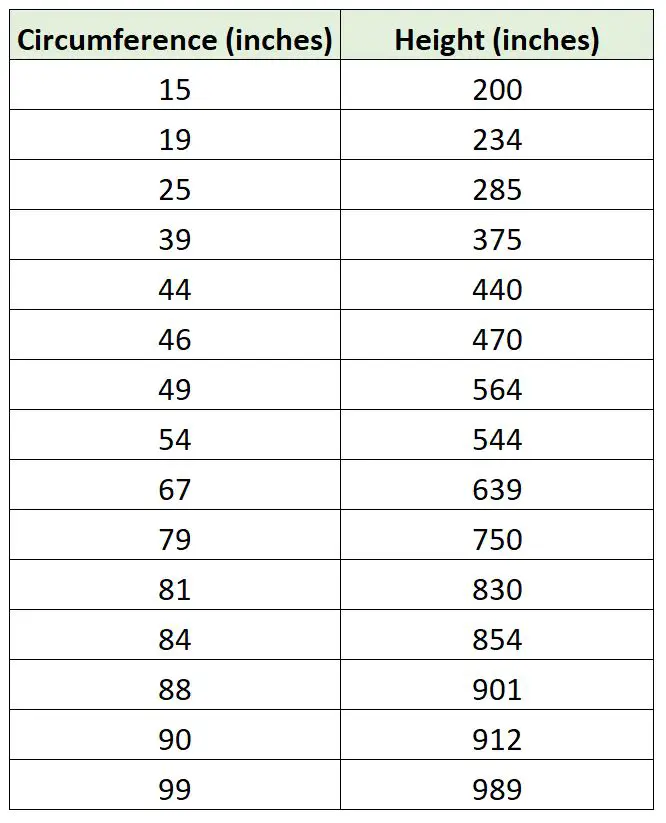
We kunnen de volgende code in R gebruiken om een eenvoudig lineair regressiemodel te fitten met een regressiemodel dat geen intercepts gebruikt en de twee regressielijnen uit te zetten:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

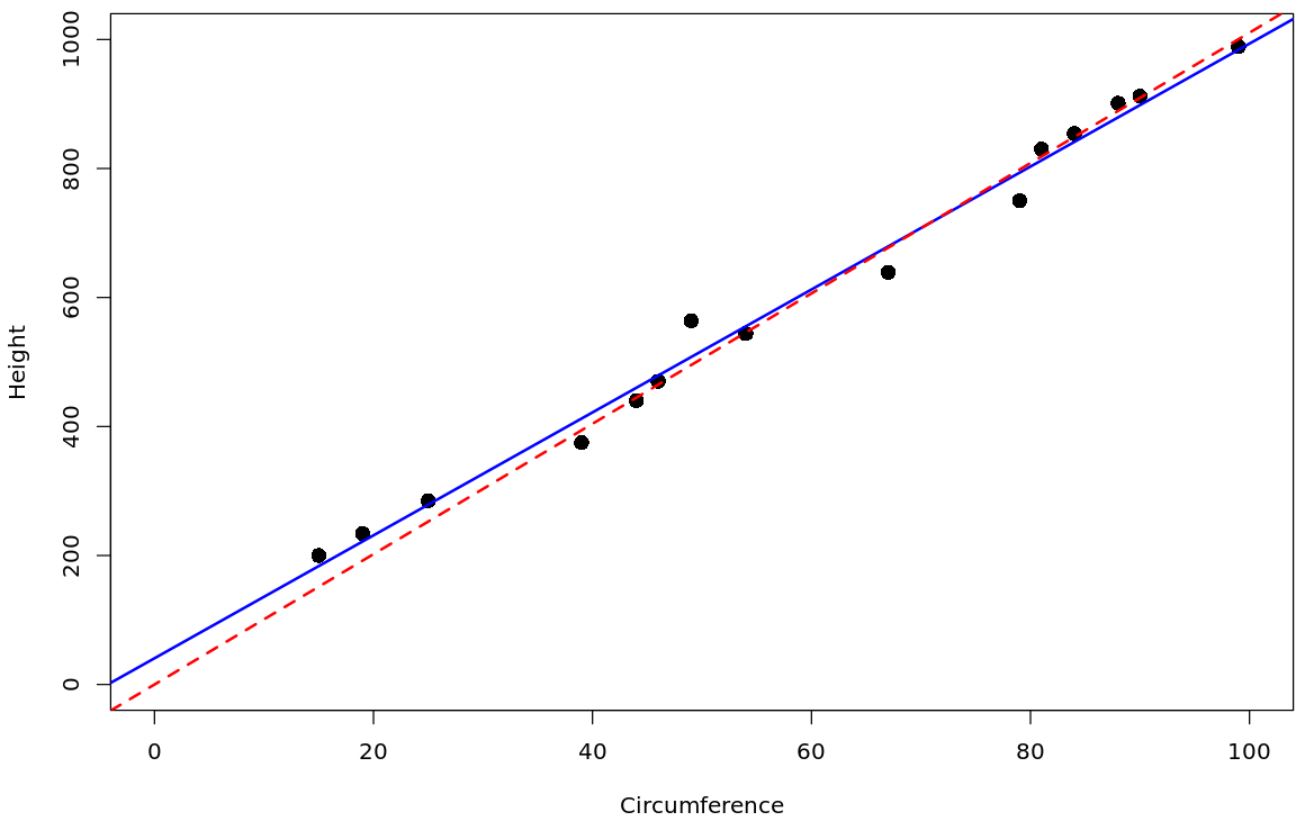
De rode stippellijn vertegenwoordigt het regressiemodel dat door de oorsprong gaat, en de blauwe ononderbroken lijn vertegenwoordigt het gewone, eenvoudige lineaire regressiemodel.

We kunnen de volgende code in R gebruiken om de coëfficiëntschattingen voor elk model te verkrijgen:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

De aangepaste vergelijking voor het eenvoudige lineaire regressiemodel is:

Hoogte = 40,6969 + 9,5296 (omtrek)

En de gepaste vergelijking voor het regressiemodel via de oorsprong is:

Hoogte = 10,1057 (omtrek)

Merk op dat de coëfficiëntschattingen voor de omtrekvariabele enigszins afwijken.

Voorzorgsmaatregelen voor het gebruik van regressie via de oorsprong

Voordat u intercept-regressie gebruikt, moet u er absoluut zeker van zijn dat een waarde van 0 voor de voorspellende variabele een waarde van 0 voor de responsvariabele impliceert. In veel scenario’s is het bijna onmogelijk om het zeker te weten.

En als je regressie via de oorsprong gebruikt om een zekere mate van vrijheid te besparen bij het schatten van de oorsprong, maakt het zelden een substantieel verschil als je steekproefomvang groot genoeg is.

Als u ervoor kiest om regressie via de oorsprong te gebruiken, zorg er dan voor dat u uw redenering schetst in uw uiteindelijke analyse of rapport.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over lineaire regressie:

Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
Een regressietabel lezen en interpreteren