Hoe u de betekenis van een regressiehelling kunt testen

Laten we zeggen dat we de volgende dataset hebben die de vierkante meters en de prijs van 12 verschillende huizen toont:

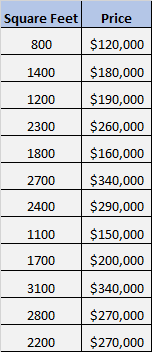
We willen weten of er een significante relatie bestaat tussen vierkante meters en prijs.

Om een idee te krijgen hoe de gegevens eruit zien, maken we eerst een spreidingsdiagram met vierkante voet op de x-as en de prijs op de y-as:

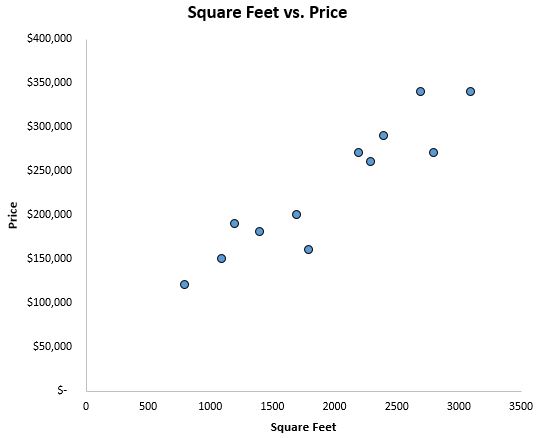
We kunnen duidelijk zien dat er een positieve correlatie bestaat tussen vierkante meters en prijs. Naarmate het aantal vierkante meters toeneemt, stijgt ook de prijs van het huis.

Om er echter achter te komen of er een statistisch significante relatie bestaat tussen vierkante meters en prijs, moeten we een eenvoudige lineaire regressie uitvoeren.

We voeren dus een eenvoudige lineaire regressie uit met vierkante voet als voorspeller en de prijs als respons en krijgen het volgende resultaat:

Of u nu een eenvoudige lineaire regressie uitvoert in Excel, SPSS, R of andere software, u krijgt een resultaat dat lijkt op het resultaat dat hierboven wordt weergegeven.

Houd er rekening mee dat een eenvoudige lineaire regressie de best passende lijn oplevert, wat de vergelijking is van de lijn die het beste ‘past’ bij de gegevens in ons spreidingsdiagram. Deze lijn met de beste pasvorm wordt gedefinieerd als:

ŷ = _b0 + _b1 x

waarbij ŷ de voorspelde waarde van de responsvariabele is, b ₀ het snijpunt is, b ₁ de regressiecoëfficiënt is en x de waarde van de voorspellende variabele is.

De waarde van b ₀ wordt gegeven door de coëfficiënt van de oorsprong, namelijk 47588,70.

De waarde van b ₁ wordt gegeven door de coëfficiënt van de voorspellende variabele Square Feet , die 93,57 is.

De best passende lijn in dit voorbeeld is dus ŷ = 47588,70+ 93,57x

Zo interpreteert u deze lijn die het beste past:

• b ₀ : Wanneer de waarde van vierkante voet nul is, is de verwachte gemiddelde prijswaarde $ 47.588,70. (In dit geval heeft het niet echt zin om het snijpunt te interpreteren, aangezien een huis nooit nul vierkante meter kan hebben)
• b ₁ : Voor elke extra vierkante meter bedraagt de gemiddelde verwachte prijsstijging € 93,57.

We weten nu dus dat voor elke extra vierkante meter de gemiddelde verwachte prijsstijging $ 93,57 bedraagt.

Om te weten of deze toename statistisch significant is, moeten we een hypothesetest uitvoeren voor B ₁ of een betrouwbaarheidsinterval construeren voor B ₁ .

Opmerking : een hypothesetest en een betrouwbaarheidsinterval zullen altijd dezelfde resultaten opleveren.

Constructie van een betrouwbaarheidsinterval voor een regressiehelling

Om een betrouwbaarheidsinterval voor een regressiehelling te construeren, gebruiken we de volgende formule:

Betrouwbaarheidsinterval = b ₁ +/- (t _{1-∝/2, n-2} ) * (standaardfout van b ₁ )

Goud:

• b ₁ is de hellingscoëfficiënt gegeven in het regressieresultaat
• (t _{1-∝/2, n-2} ) is de kritische t-waarde voor het 1-∝ betrouwbaarheidsniveau met n-2 vrijheidsgraden waarbij n het totale aantal waarnemingen in onze dataset is
• (standaardfout van b ₁ ) is de standaardfout van b ₁ gegeven in het regressieresultaat

In ons voorbeeld ziet u hoe u een betrouwbaarheidsinterval van 95% kunt construeren voor B ₁ :

• b ₁ is 93,57 uit de regressie-uitvoer.
• Omdat we een betrouwbaarheidsinterval van 95% gebruiken, ∝ = 0,05 en n-2 = 12-2 = 10, dus t _{0,975, 10} is 2,228 volgens de t-verdelingstabel
• (de standaardfout van _b1 ) is 11,45 op basis van de regressie-uitvoer

Ons 95% betrouwbaarheidsinterval voor B ₁ is dus:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Dit betekent dat we er 95% zeker van zijn dat de werkelijke gemiddelde prijsstijging voor elke extra vierkante meter tussen €68,06 en €119,08 ligt.

Houd er rekening mee dat $ 0 niet in dit interval ligt, dus de relatie tussen vierkante meters en prijs is statistisch significant bij een betrouwbaarheidsniveau van 95%.

Een hypothesetest uitvoeren voor een regressiehelling

Om een hypothesetest voor een regressiehelling uit te voeren, volgen we de vijf standaardstappen voor elke hypothesetest :

Stap 1. Formuleer de hypothesen.

De nulhypothese (H0): B ₁ = 0

De alternatieve hypothese: (Ha): B ₁ ≠ 0

Stap 2. Bepaal een significantieniveau dat u wilt gebruiken.

Omdat we in het vorige voorbeeld een betrouwbaarheidsinterval van 95% hebben geconstrueerd, zullen we hier de equivalente aanpak gebruiken en ervoor kiezen een significantieniveau van 0,05 te gebruiken.

Stap 3. Zoek de teststatistiek en de bijbehorende p-waarde.

In dit geval is de teststatistiek t = coëfficiënt van b ₁ / standaardfout van b ₁ met n-2 vrijheidsgraden. We kunnen deze waarden vinden uit het regressieresultaat:

De teststatistiek t = 92,89 / 13,88 = 6,69.

Met behulp van de T-score naar P-waardecalculator met een score van 6,69 met 10 vrijheidsgraden en een tweezijdige test, is de p-waarde = 0,000 .

Stap 4. Verwerp de nulhypothese of verwerp deze niet.

Omdat de p-waarde onder ons significantieniveau van 0,05 ligt, verwerpen we de nulhypothese.

Stap 5. Interpreteer de resultaten.

Sinds we de nulhypothese hebben verworpen, hebben we voldoende bewijs om te zeggen dat de werkelijke gemiddelde prijsstijging voor elke extra vierkante meter niet nul is.