Wat is een regressor? (definitie & voorbeelden)

In de statistiek is een regressor de naam die wordt gegeven aan elke variabele in een regressiemodel dat wordt gebruikt om een responsvariabele te voorspellen.

Een regressor wordt ook wel genoemd:

• Eenverklarende variabele
• Een onafhankelijke variabele
• Een gemanipuleerde variabele
• Een variabele voorspelling
• Een karakter eigenschap

Al deze termen worden door elkaar gebruikt, afhankelijk van het type vakgebied waarin u werkt: statistiek, machinaal leren, econometrie, biologie, enz.

Opmerking: Soms wordt een responsvariabele ‚regresseerbaar‘ genoemd.

Regressoren in regressiemodellen

De meeste regressiemodellen hebben de volgende vorm:

Y = β ₀ + B ₁ x ₁ + B ₂ x ₂ + B ₃ x ₃ + ε

Goud:

• Y: de responsvariabele
• β _i : de coëfficiënten voor de regressoren
• x _i : De regressoren
• ε: De foutterm

Het punt van het bouwen van een regressiemodel is om te begrijpen hoe veranderingen in een regressor leiden tot veranderingen in een responsvariabele (of ‘regressor’).

Merk op dat regressiemodellen een of meer regressoren kunnen hebben.

Als er slechts één regressor is, wordt het model een eenvoudig lineair regressiemodel genoemd en als er meerdere regressors zijn, wordt het model een meervoudig lineair regressiemodel genoemd om aan te geven dat er meerdere regressors zijn.

De volgende voorbeelden illustreren hoe regressoren in verschillende regressiemodellen moeten worden geïnterpreteerd.

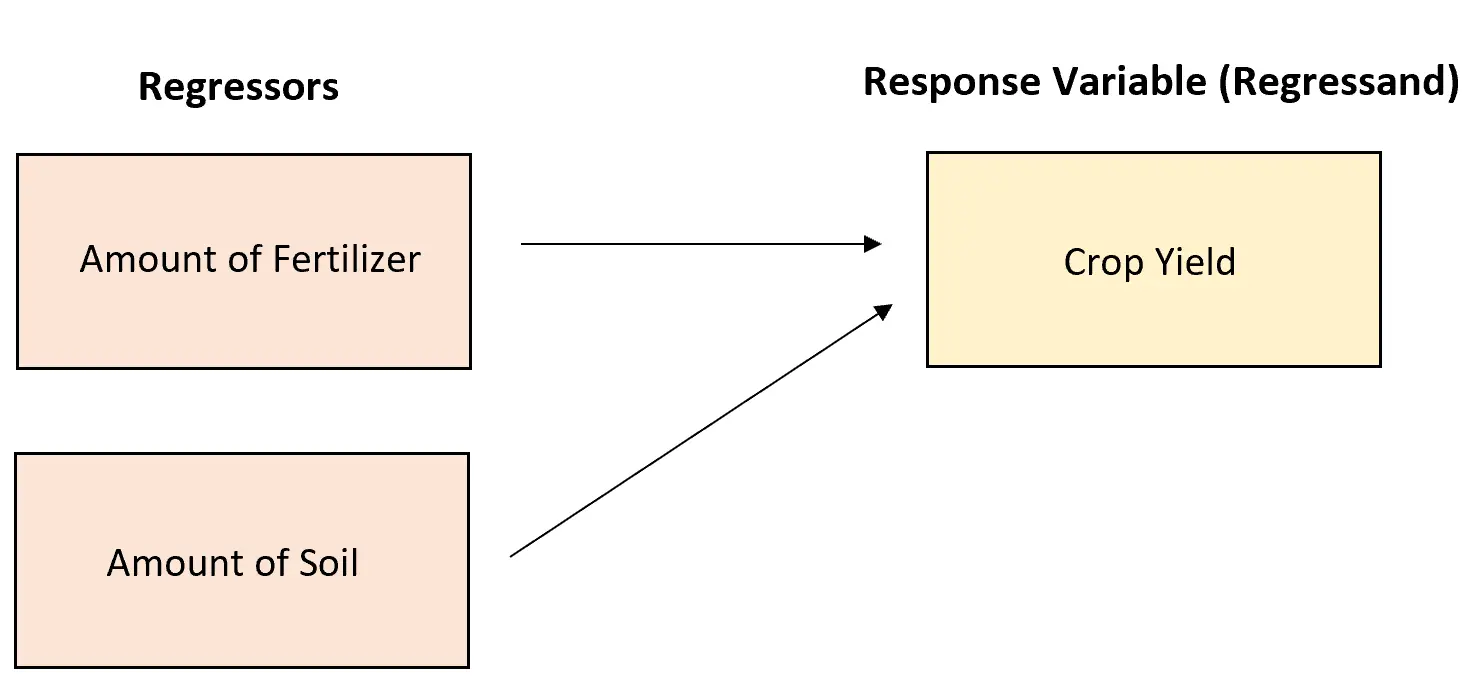
Voorbeeld 1: Gewasopbrengst

Stel dat een boer inzicht wil krijgen in de factoren die de totale gewasopbrengst (in kilo’s) beïnvloeden. Het verzamelt gegevens en bouwt het volgende regressiemodel:

Gewasopbrengst = 154,34 + 3,56*(kg kunstmest) + 1,89*(kg grond)

Dit model heeft twee regressoren: Kunstmest en Bodem.

Hier leest u hoe u deze twee regressoren interpreteert:

• Meststof: Voor elk extra pond kunstmest dat wordt gebruikt, neemt de gewasopbrengst met gemiddeld 3,56 pond toe, ervan uitgaande dat de hoeveelheid grond constant blijft.
• Bodem: Voor elk extra pond grond dat wordt gebruikt, neemt de gewasopbrengst met gemiddeld 1,89 pond toe, ervan uitgaande dat de hoeveelheid kunstmest constant blijft.

Voorbeeld 2: Examenresultaten

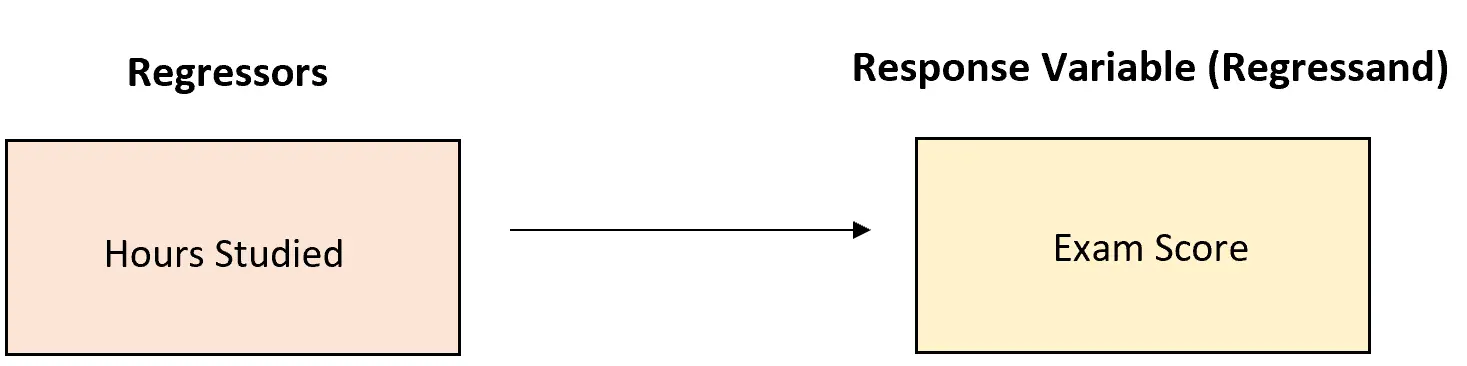
Stel dat een hoogleraar wil begrijpen hoe het aantal gestudeerde uren de examenscores beïnvloedt. Het verzamelt gegevens en bouwt het volgende regressiemodel:

Examenscore = 68,34 + 3,44* (uren gestudeerd)

Dit model bevat een regressor: bestudeerde uren. We interpreteren de coëfficiënt van deze regressor zo dat voor elk extra bestudeerd uur de examenscore met gemiddeld 3,44 punten stijgt.

Aanvullende bronnen

Hoe regressiecoëfficiënten te interpreteren
Hoe u de betekenis van een regressiehelling kunt testen
Een regressietabel lezen en interpreteren