Rekenkundig gemiddelde
Hier leggen we uit wat het rekenkundig gemiddelde is en hoe het wordt berekend. U vindt voorbeelden van rekenkundige gemiddelden en zelfs een rekenmachine om het rekenkundig gemiddelde van een statistische steekproef te vinden. Ten slotte kunt u zien wat de eigenschappen zijn van dit type gemiddelde en hoe het rekenkundig gemiddelde wordt verkregen met gegevens die in intervallen zijn gegroepeerd.
Wat is het rekenkundige gemiddelde?
Het rekenkundig gemiddelde is een centraal waardekenmerk van een reeks statistische gegevens. Om het rekenkundig gemiddelde te berekenen, worden alle waarden opgeteld en gedeeld door het totale aantal gegevens.
Bovendien is het rekenkundig gemiddelde een van de belangrijkste indicatoren die worden gebruikt om een statistische studie van een steekproef uit te voeren.
De formule voor het rekenkundig gemiddelde is daarom als volgt:
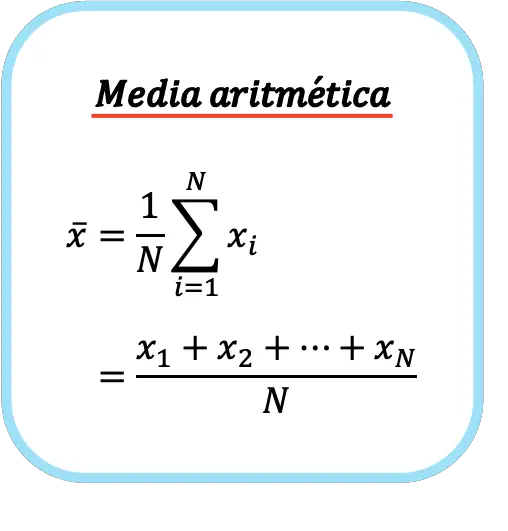
Het symbool voor het rekenkundig gemiddelde is een horizontale band boven de letter x.
![]()
U kunt het steekproefgemiddelde ook onderscheiden van het populatiegemiddelde met het gemiddelde symbool: het gemiddelde van een steekproef wordt uitgedrukt met het symbool
![]()
Aan de andere kant gebruiken we voor het gemiddelde van een bevolking de Griekse letter
![]()
Opgemerkt moet worden dat het rekenkundig gemiddelde van een populatie gelijk is aan de verwachte waarde van de statistische variabele.
Het rekenkundig gemiddelde, ook wel het rekenkundig gemiddelde genoemd, is niet het enige type gemiddelde dat bestaat; er zijn onder meer ook het gewogen gemiddelde, het kwadratische gemiddelde, het geometrische gemiddelde en het harmonische gemiddelde. Hoe elk van deze wordt berekend, kunt u zien in de zoekmachine van onze website.
Hoe het rekenkundig gemiddelde te berekenen
Om het rekenkundig gemiddelde te berekenen, moeten de volgende stappen worden uitgevoerd:
- Voeg alle statistische gegevens uit het monster toe.
- Deel de vorige som door het totale aantal gegevens.
- Het verkregen resultaat is het rekenkundig gemiddelde van de statistische steekproef.
👉 U kunt de onderstaande rekenmachine gebruiken om het rekenkundig gemiddelde van elke dataset te berekenen.
Voorbeeld van het berekenen van het rekenkundig gemiddelde
Gegeven de definitie van rekenkundig gemiddelde, zullen we zien hoe we het rekenkundig gemiddelde van een reeks gegevens kunnen verkrijgen door stap voor stap een voorbeeld op te lossen.
- Een leerling behaalde in een schooljaar de volgende cijfers: voor wiskunde een 9, voor taal een 7, voor geschiedenis een 6, voor economie een 8 en voor natuurkunde een 7,5. Wat is het rekenkundig gemiddelde van al jouw cijfers?
Om het rekenkundig gemiddelde te vinden, moeten we alle cijfers bij elkaar optellen en vervolgens delen door het totale aantal vakken in de cursus, dat is 5. Daarom passen we de formule voor het rekenkundig gemiddelde toe:
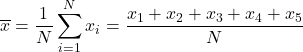
We vervangen de gegevens in de formule en berekenen het rekenkundig gemiddelde:
![]()
Zoals u kunt zien, wordt in het rekenkundig gemiddelde aan elke waarde hetzelfde gewicht toegekend, dat wil zeggen dat elk stukje gegevens binnen het geheel hetzelfde gewicht heeft.
Rekenkundige gemiddelde rekenmachine
Voer gegevens uit een statistisch monster in de volgende rekenmachine in om het rekenkundig gemiddelde ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.
Rekenkundig gemiddelde voor gegroepeerde gegevens
Met gegroepeerde gegevens bedoelen we dat de gegevens zijn gestructureerd als groepen of intervallen. Dit gebeurt meestal wanneer de statistische steekproefomvang erg groot is.
De berekening van het rekenkundig gemiddelde varieert dus enigszins wanneer de gegevens worden gegroepeerd, ook al is het concept hetzelfde.
Om het rekenkundig gemiddelde te berekenen van gegevens die in intervallen zijn gegroepeerd , moet de klassescore van elke groep worden vermenigvuldigd met de absolute frequentie ervan en vervolgens worden gedeeld door de som van alle absolute frequenties.
![]()
Let op: De klassescore van een interval wordt berekend door de som van de eindpunten van het interval te delen door twee. De klassenoot van het interval [3,7) zou bijvoorbeeld zijn:
![]()
Zodat u kunt zien hoe dit wordt gedaan, vindt u hieronder een opgeloste oefening over het rekenkundig gemiddelde van gegevens gegroepeerd in intervallen:
- We willen het gewicht van een groep statistisch bestuderen, hiervoor hebben we een representatieve groep van 81 mensen geïnterviewd en hebben we de volgende gegevens verkregen:
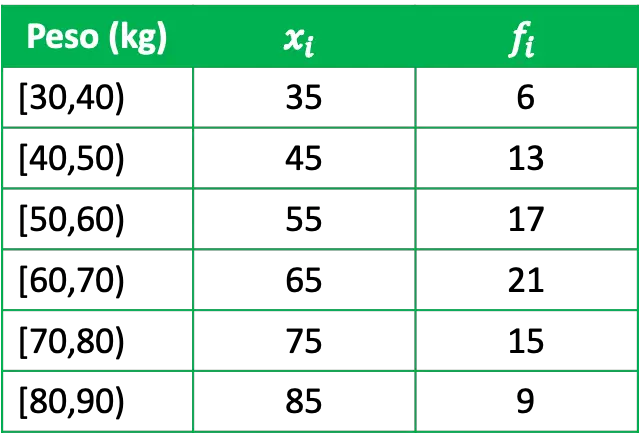
Waarbij x i de klassescore van elke groep is en f i de absolute frequentie ervan, dat wil zeggen het aantal mensen dat een gewicht heeft in dit interval.
Om het rekenkundig gemiddelde te bepalen, is het noodzakelijk om een kolom in de frequentietabel toe te voegen die het product is van de klassenoten door hun respectieve absolute frequenties:
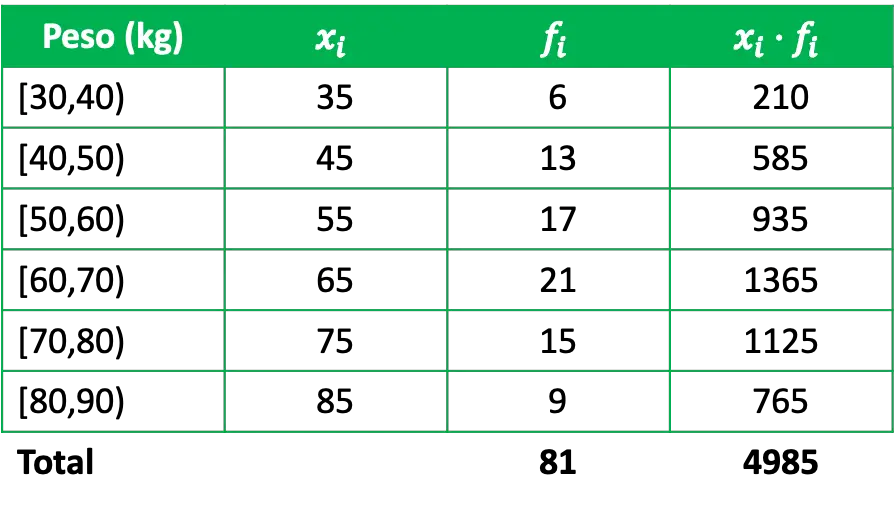
Om het rekenkundig gemiddelde van de gegroepeerde gegevens te berekenen, deelt u eenvoudigweg de som van de producten van de klassenoten op basis van hun frequenties door het totale aantal gegevens:
![]()
Eigenschappen van het rekenkundig gemiddelde
Het rekenkundig gemiddelde heeft de volgende kenmerken:
- De som van de afwijkingen van alle gegevens in een verdeling van het gemiddelde resulteert in nul.
![]()
- Als we hetzelfde bedrag toevoegen aan alle gegevens in een steekproef, neemt het steekproefgemiddelde met dat bedrag toe.
- Hetzelfde gebeurt bij vermenigvuldiging: als je alle waarden in een steekproef met een getal vermenigvuldigt, wordt het steekproefgemiddelde met dat getal vermenigvuldigd.
- Het rekenkundig gemiddelde kan alleen worden berekend in kwantitatieve variabelen . Met andere woorden: je kunt niet het gemiddelde nemen van kwalitatieve variabelen.
- Het rekenkundig gemiddelde zal altijd een waarde zijn tussen het minimum en het maximum van een verdeling.
![]()
- Dit type gemiddelde is zeer gevoelig voor zeer hoge of zeer lage waarden, waardoor een uitschieter het resultaat van het rekenkundig gemiddelde aanzienlijk verandert.
- Het rekenkundig gemiddelde van een dataset is altijd gelijk aan of groter dan het geometrische gemiddelde van dezelfde dataset.
![]()
Bereken het rekenkundig gemiddelde met Excel
Het berekenen van het rekenkundig gemiddelde in Excel is heel eenvoudig, omdat u alleen maar de gegevens op een blad hoeft in te voeren en de functie GEMIDDELDE te gebruiken.
Om bijvoorbeeld het rekenkundig gemiddelde te bepalen van de gegevens uit de eerste opgeloste oefening die we hebben uitgelegd, kopieert u eenvoudigweg alle gegevens naar een Excel-document en schrijft u de volgende formule in een cel: =GEMIDDELDE(9;7;5; 8;7 ,5) . De functie retourneert het rekenkundig gemiddelde van de gegevens, namelijk 7,3.
Het is duidelijk dat het veel sneller is om het rekenkundig gemiddelde van bepaalde getallen te vinden met het Excel-programma dan om het met de hand te berekenen, vooral als de steekproefomvang erg groot is.