Hoe de relatieve standaarddeviatie in excel te berekenen

Relatieve standaardafwijking is een maatstaf voor de standaardafwijking van de steekproef ten opzichte van het steekproefgemiddelde voor een bepaalde gegevensset.

Het wordt als volgt berekend:

Relatieve standaardafwijking = s/ x * 100%

Goud:

• s: standaardafwijking van het monster
• x : steekproefgemiddelde

Deze metriek geeft ons een idee van hoe nauw waarnemingen rond het gemiddelde zijn geclusterd.

Stel bijvoorbeeld dat de standaardafwijking van een dataset 4 is. Als het gemiddelde 400 is, dan is de relatieve standaardafwijking 4/400 * 100% = 1%. Dit betekent dat de waarnemingen strak rond het gemiddelde zijn geclusterd.

Een dataset met een standaardafwijking van 40 en een gemiddelde van 400 zal echter een relatieve standaardafwijking van 10% hebben. Dit betekent dat de waarnemingen veel meer rond het gemiddelde verdeeld zijn vergeleken met de vorige dataset.

Deze zelfstudie geeft een voorbeeld van het berekenen van de relatieve standaardafwijking in Excel.

Voorbeeld: relatieve standaardafwijking in Excel

Stel dat we de volgende gegevensset in Excel hebben:

De volgende formules laten zien hoe u het steekproefgemiddelde, de steekproefstandaardafwijking en de steekproef relatieve standaardafwijking van de gegevensset kunt berekenen:

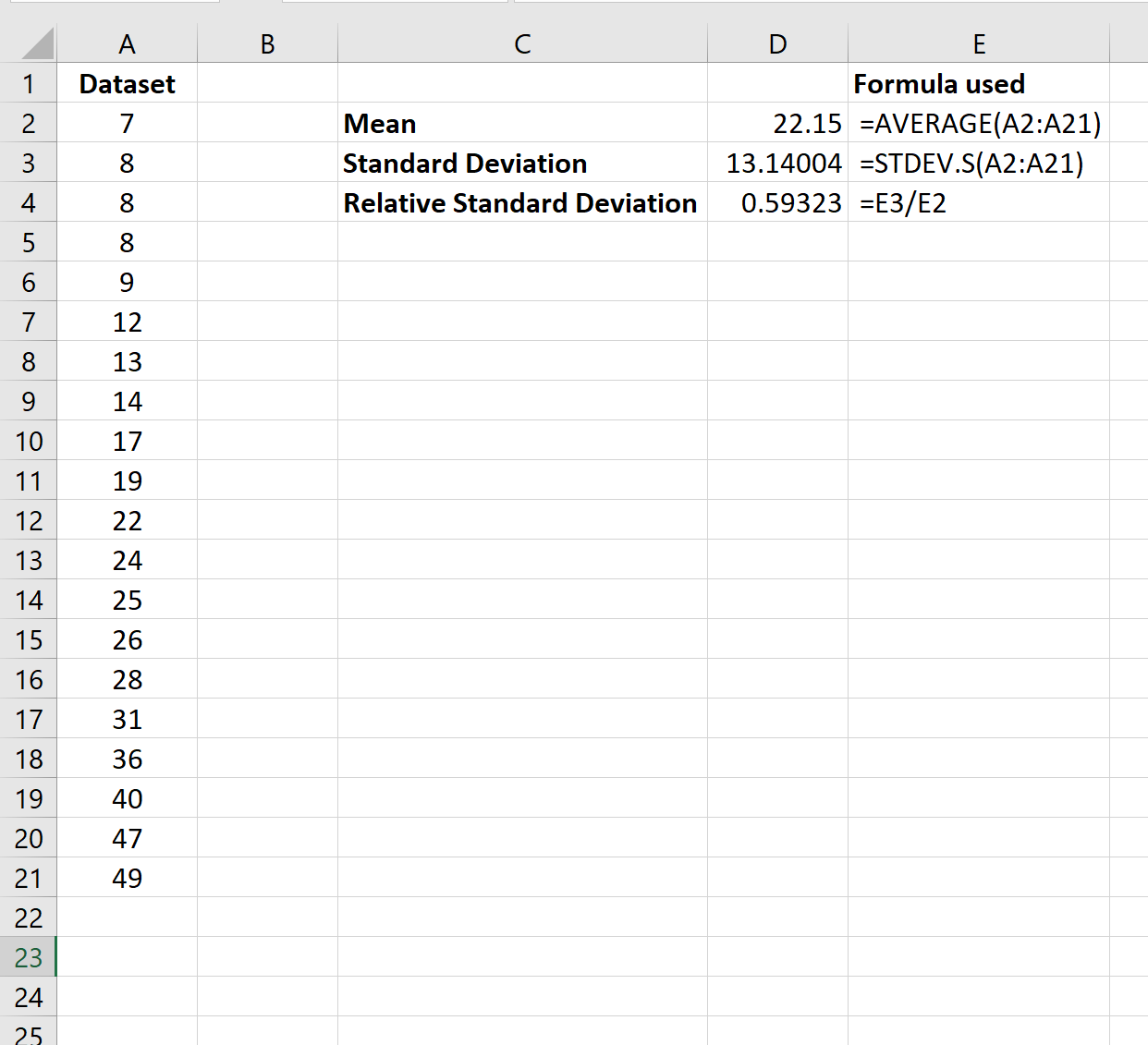
De relatieve standaardafwijking blijkt 0,59 te zijn.

Dit vertelt ons dat de standaardafwijking van de dataset 59% is van de grootte van het datasetgemiddelde. Dit getal is vrij groot, wat aangeeft dat de waarden redelijk verspreid zijn rond het steekproefgemiddelde.

Als we meerdere datasets hebben, kunnen we dezelfde formule gebruiken om de relatieve standaardafwijking (RSD) voor elke dataset te berekenen en de RSD’s tussen de datasets te vergelijken:

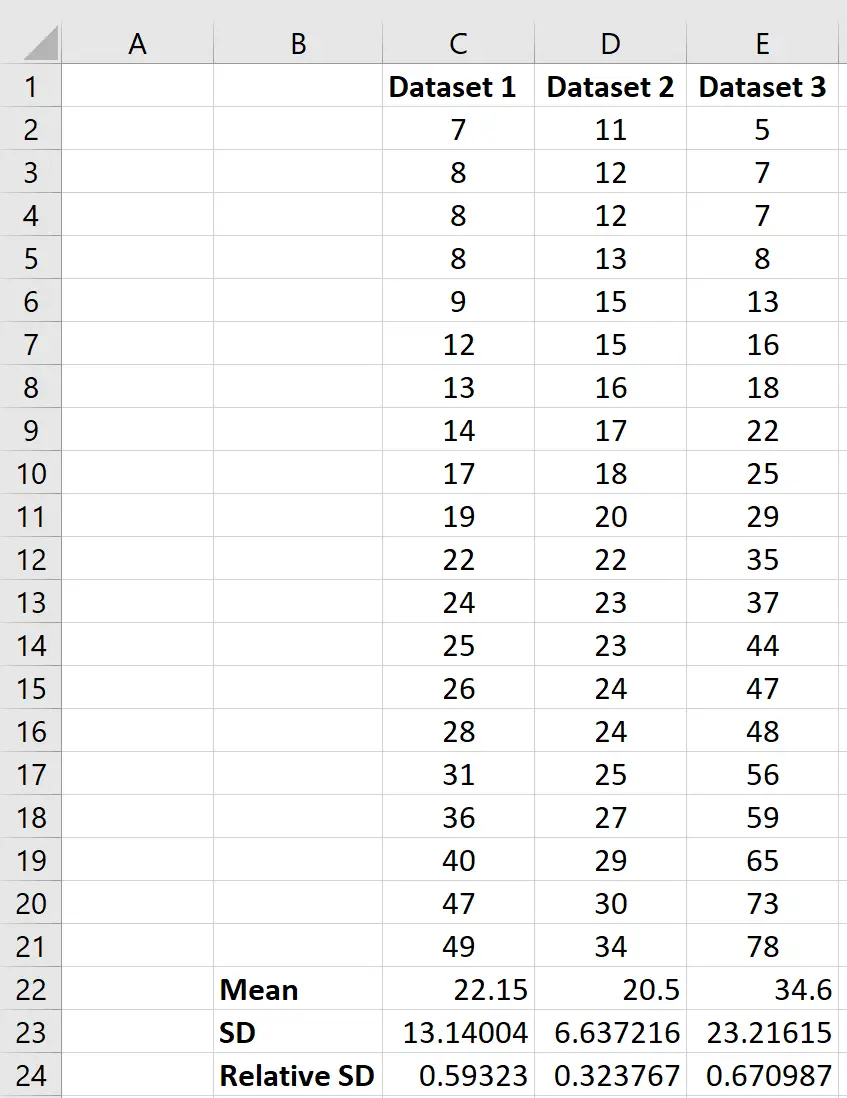
We kunnen zien dat dataset 3 de grootste relatieve standaardafwijking heeft, wat aangeeft dat de waarden in deze dataset het meest verspreid zijn ten opzichte van het datasetgemiddelde.

Omgekeerd kunnen we zien dat Dataset 2 de kleinste relatieve standaardafwijking heeft, wat aangeeft dat de waarden in deze dataset het minst verspreid zijn ten opzichte van het gemiddelde van deze specifieke dataset.

Meer Excel-tutorials vindt u hier .