Wat zijn residuen in de statistiek?

Een residu is het verschil tussen een waargenomen waarde en een voorspelde waarde inregressieanalyse .

Het wordt als volgt berekend:

Residueel = Waargenomen waarde – Voorspelde waarde

Bedenk dat het doel van lineaire regressie het kwantificeren van de relatie tussen een of meer voorspellende variabelen en een responsvariabele is. Om dit te doen, zoekt lineaire regressie naar de lijn die het beste ‘past’ bij de gegevens, de zogenaamde kleinste kwadratenregressielijn .

Deze lijn produceert een voorspelling voor elke waarneming in de dataset, maar het is onwaarschijnlijk dat de voorspelling van de regressielijn exact overeenkomt met de waargenomen waarde.

Het verschil tussen de voorspelling en de waargenomen waarde is het residu. Als we de waargenomen waarden uitzetten en de aangepaste regressielijn over elkaar leggen, zijn de residuen voor elke waarneming de verticale afstand tussen de waarneming en de regressielijn:

Een waarneming heeft een positief residu als de waarde ervan groter is dan de voorspelde waarde van de regressielijn.

Omgekeerd heeft een waarneming een negatief residu als de waarde ervan kleiner is dan de voorspelde waarde van de regressielijn.

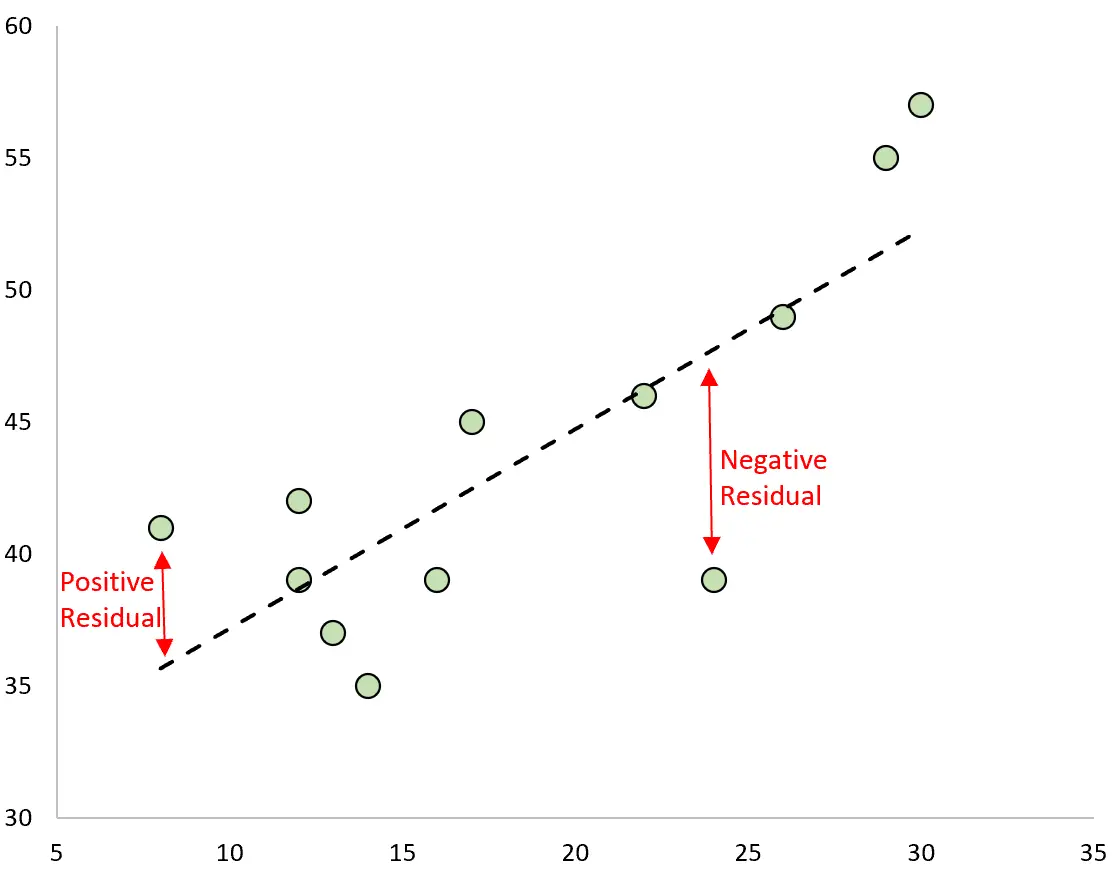
Sommige waarnemingen zullen positieve residuen hebben, terwijl andere negatieve residuen zullen hebben, maar alle residuen zullen opgeteld nul zijn .

Voorbeeld van het berekenen van residuen

Stel dat we de volgende dataset hebben met in totaal 12 waarnemingen:

Als we statistische software (zoals R , Excel , Python , Stata , etc.) gebruiken om een lineaire regressielijn in deze gegevensset te passen, zullen we ontdekken dat de best passende lijn blijkt te zijn:

y = 29,63 + 0,7553x

Met behulp van deze lijn kunnen we de voorspelde waarde voor elke Y-waarde berekenen op basis van de waarde van X. De voorspelde waarde van de eerste waarneming zou bijvoorbeeld zijn:

j = 29,63 + 0,7553*(8) = 35,67

We kunnen dan het residu voor deze waarneming als volgt berekenen:

Residueel = Waargenomen waarde – Voorspelde waarde = 41 – 35,67 = 5,33

We kunnen dit proces herhalen om het residu voor elke waarneming te vinden:

Als we een spreidingsdiagram maken om de waarnemingen met de gepaste regressielijn te visualiseren, zullen we zien dat sommige waarnemingen boven de lijn liggen, terwijl andere onder de lijn liggen:

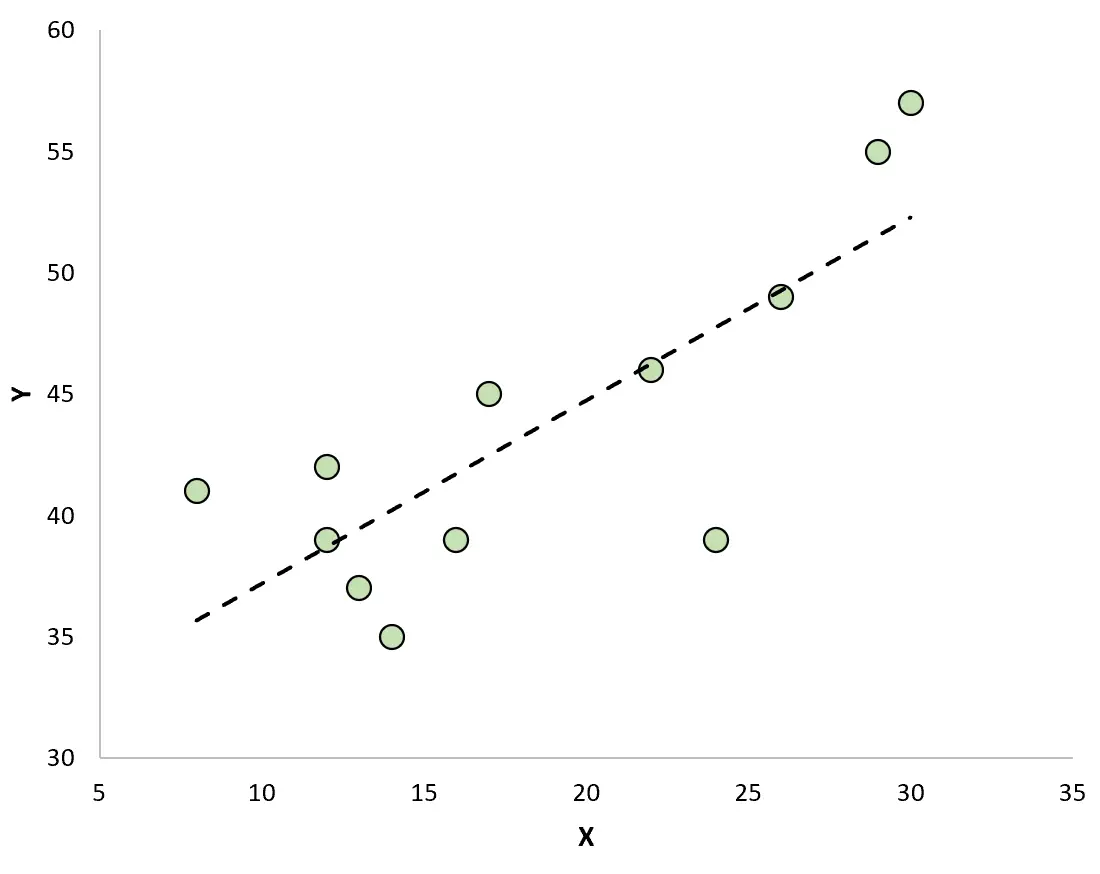
Eigenschappen van residuen

Residuen hebben de volgende eigenschappen:

• Elke waarneming in een dataset heeft een overeenkomstig residu. Dus als een dataset in totaal 100 waarnemingen bevat, zal het model 100 voorspelde waarden produceren, wat in totaal 100 residuen oplevert.
• De som van alle residuen is nul.
• De gemiddelde waarde van de reststoffen is nul.

Hoe worden reststoffen in de praktijk gebruikt?

In de praktijk worden residuen om drie verschillende redenen gebruikt bij regressie:

1. Evalueer de geschiktheid van het model.

Zodra we een gepaste regressielijn hebben gemaakt, kunnen we de residuele som van de kwadraten (RSS) berekenen, wat de som is van alle gekwadrateerde residuen. Hoe lager de RSS, hoe beter het regressiemodel bij de gegevens past.

2. Controleer de normaliteitsaanname.

Een van de belangrijkste aannames van lineaire regressie is dat de residuen normaal verdeeld zijn.

Om deze hypothese te testen, kunnen we een QQ-plot maken. Dit is een soort plot dat we kunnen gebruiken om te bepalen of de residuen van een model al dan niet een normale verdeling volgen.

Als de punten op de grafiek grofweg een rechte diagonale lijn vormen, wordt aan de aanname van normaliteit voldaan.

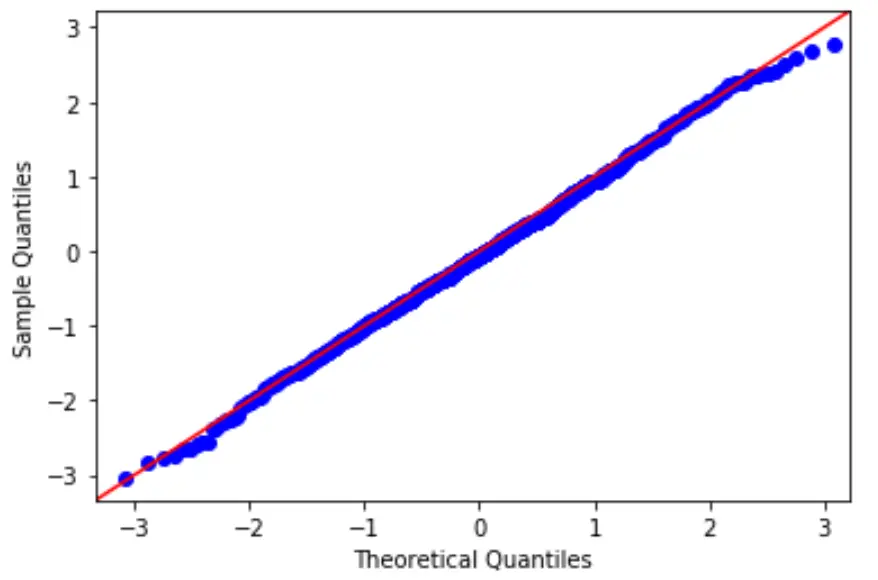
3. Controleer de aanname van homoscedasticiteit.

Een andere belangrijke aanname van lineaire regressie is dat de residuen een constante variantie hebben op elk niveau van x. Dit heet homoscedasticiteit. Wanneer dit niet het geval is, lijden de residuen aan heteroscedasticiteit .

Om te controleren of aan deze aanname wordt voldaan, kunnen we een residuenplot maken. Dit is een spreidingsdiagram dat de residuen weergeeft ten opzichte van de voorspelde waarden van het model.

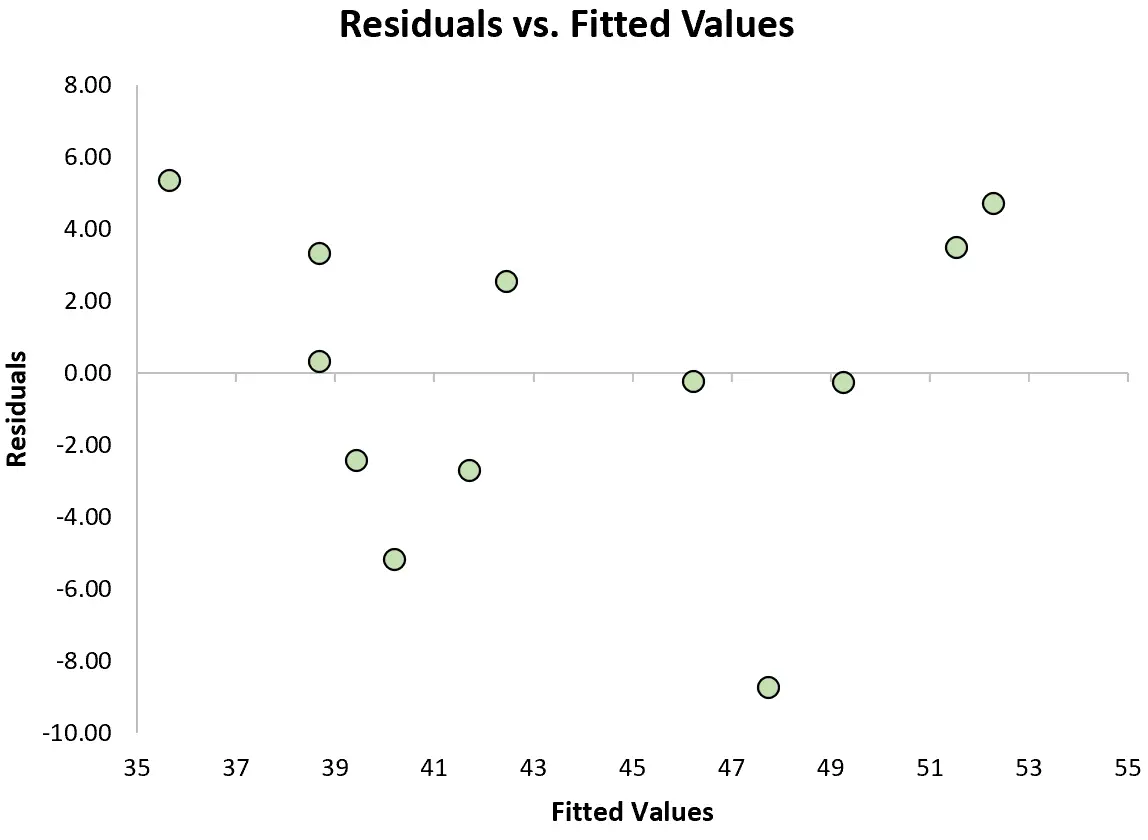
Als de residuen ongeveer gelijkmatig verdeeld zijn rond nul in de grafiek zonder duidelijke trend, dan zeggen we over het algemeen dat aan de aanname van homoscedasticiteit is voldaan.

Aanvullende bronnen

Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
De vier aannames van lineaire regressie
Hoe u een restplot in Excel maakt