Hoe gestudentiseerde residuen in r te berekenen

Een studentenresidu is eenvoudigweg een residu gedeeld door de geschatte standaarddeviatie.

In de praktijk zeggen we over het algemeen dat elke waarneming in een dataset waarvan het studentenresidu groter is dan de absolute waarde van 3, een uitbijter is.

We kunnen snel de gestudentiseerde residuen van elk regressiemodel in R verkrijgen met behulp van de functie studres() uit het MASS-pakket, dat de volgende syntaxis gebruikt:

Studres (model)

waarbij model elk lineair model vertegenwoordigt.

Voorbeeld: het berekenen van gestudentiseerde residuen in R

Stel dat we het volgende eenvoudige lineaire regressiemodel in R bouwen, met behulp van de ingebouwde mtcars- dataset:

 #build simple linear regression model
model <- lm(mpg ~ disp, data=mtcars)

We kunnen de functie studres() uit het MASS-pakket gebruiken om de gestudentiseerde residuen voor elke observatie in de dataset te berekenen:

 library (MASS)

#calculate studentized residuals
stud_resids <- studres(model)

#view first three studentized residuals
head(stud_resids, 3)

    Mazda RX4 Mazda RX4 Wag Datsun 710 
   -0.6236250 -0.6236250 -0.7405315 

We kunnen ook een snelle grafiek maken van de waarden van de voorspellende variabelen tegen de overeenkomstige bestudeerde residuen:

 #plot predictor variable vs. studentized residuals
plot(mtcars$disp, stud_resids, ylab=' Studentized Residuals ', xlab=' Displacement ') 

#add horizontal line at 0
abline(0, 0) 

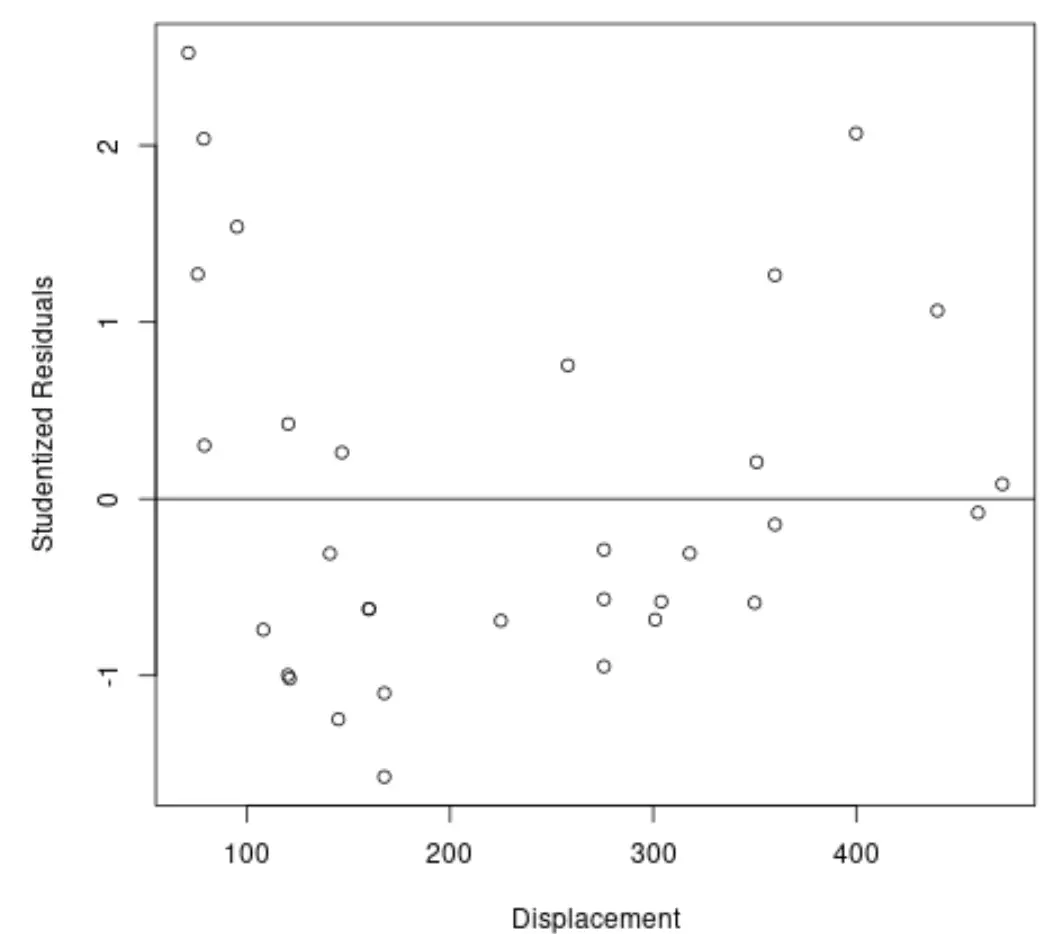
Uit de grafiek kunnen we zien dat geen van de waarnemingen een leerlingresidu heeft met een absolute waarde groter dan 3, dus er zijn geen duidelijke uitschieters in de dataset.

We kunnen ook de gestudentiseerde residuen van elke waarneming in de originele dataset toevoegen als we dat willen:

 #add studentized residuals to orignal dataset
final_data <- cbind (mtcars[c(' mpg ', ' disp ')], stud_resids)

#view final dataset
head(final_data)

                   mpg disp stud_resids
Mazda RX4 21.0 160 -0.6236250
Mazda RX4 Wag 21.0 160 -0.6236250
Datsun 710 22.8 108 -0.7405315
Hornet 4 Drive 21.4 258 0.7556078
Hornet Sportabout 18.7 360 1.2658336
Valiant 18.1 225 -0.6896297

We kunnen vervolgens elke waarneming sorteren van groot naar klein op basis van het studentenresidu om een idee te krijgen van welke waarnemingen het dichtst bij de uitschieters liggen:

 #sort studentized residuals descending
final_data[ order (-stud_resids),]

                     mpg disp stud_resids
Toyota Corolla 33.9 71.1 2.52397102
Pontiac Firebird 19.2 400.0 2.06825391
Fiat 128 32.4 78.7 2.03684699
Lotus Europa 30.4 95.1 1.53905536
Honda Civic 30.4 75.7 1.27099586
Hornet Sportabout 18.7 360.0 1.26583364
Chrysler Imperial 14.7 440.0 1.06486066
Hornet 4 Drive 21.4 258.0 0.75560776
Porsche 914-2 26.0 120.3 0.42424678
Fiat X1-9 27.3 79.0 0.30183728
Merc 240D 24.4 146.7 0.26235893
Ford Pantera L 15.8 351.0 0.20825609
Cadillac Fleetwood 10.4 472.0 0.08338531
Lincoln Continental 10.4 460.0 -0.07863385
Duster 360 14.3 360.0 -0.14476167
Merc 450SL 17.3 275.8 -0.28759769
Dodge Challenger 15.5 318.0 -0.30826585
Merc 230 22.8 140.8 -0.30945955
Merc 450SE 16.4 275.8 -0.56742476
AMC Javelin 15.2 304.0 -0.58138205
Camaro Z28 13.3 350.0 -0.58848471
Mazda RX4 Wag 21.0 160.0 -0.62362497
Mazda RX4 21.0 160.0 -0.62362497
Maserati Bora 15.0 301.0 -0.68315010
Valiant 18.1 225.0 -0.68962974
Datsun 710 22.8 108.0 -0.74053152
Merc 450SLC 15.2 275.8 -0.94814699
Toyota Corona 21.5 120.1 -0.99751166
Volvo 142E 21.4 121.0 -1.01790487
Merc 280 19.2 167.6 -1.09979261
Ferrari Dino 19.7 145.0 -1.24732999
Merc 280C 17.8 167.6 -1.57258064

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe maak je een restplot in R