Wat is een rest-/hefboomgrafiek? (definitie & #038; voorbeeld)

Een grafiek van residuen versus hefboomwerking is een soort diagnostische grafiek waarmee we invloedrijke observaties in een regressiemodel kunnen identificeren.

Hier ziet u hoe dit type plot verschijnt in de statistische programmeertaal R:

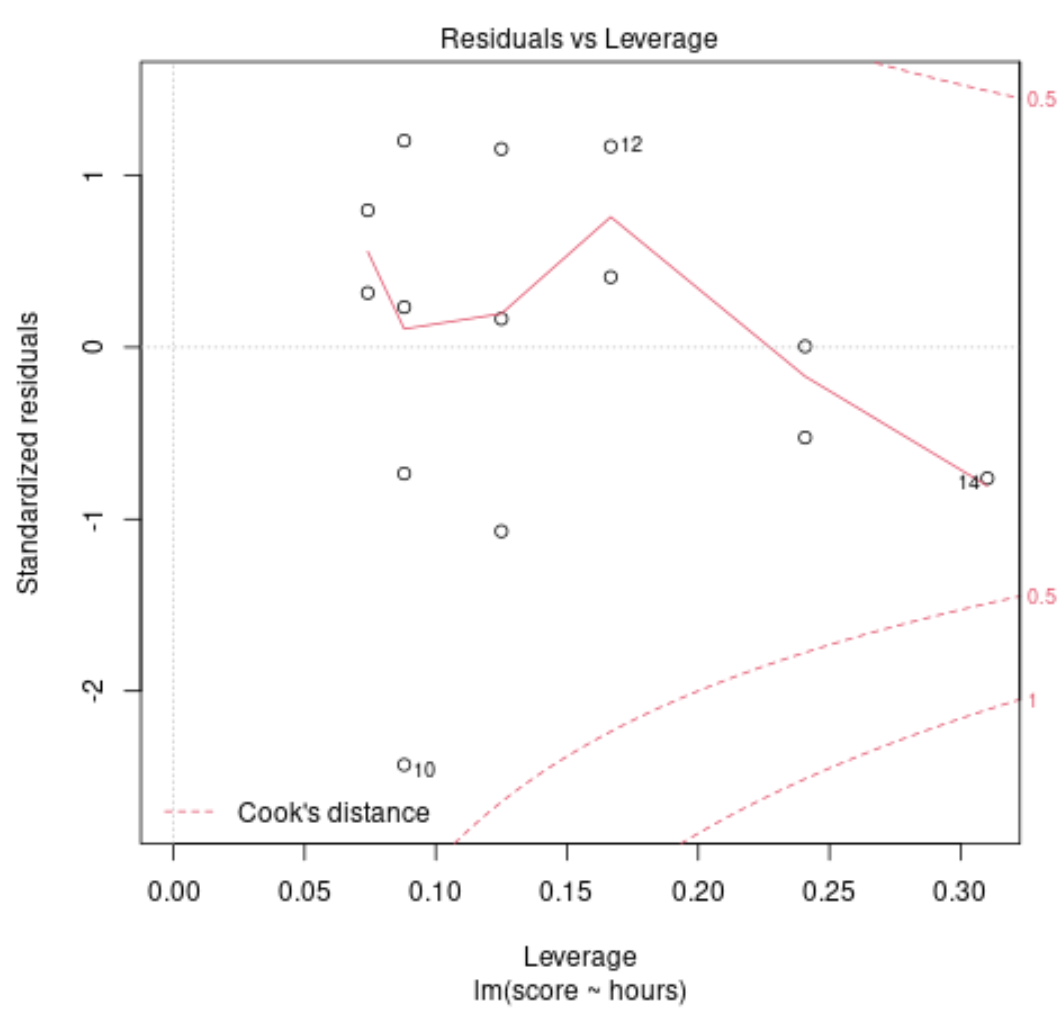
Elke waarneming in de dataset wordt weergegeven als een enkel punt in de grafiek. De x-as toont de hefboomwerking van elk punt en de y-as toont het gestandaardiseerde residu van elk punt.

Hefboomwerking verwijst naar de mate waarin de coëfficiënten van het regressiemodel zouden veranderen als een bepaalde observatie uit de dataset zou worden verwijderd.

Waarnemingen met een hoge hefboomwerking hebben een sterke invloed op de coëfficiënten van het regressiemodel. Als we deze waarnemingen verwijderen, zouden de modelcoëfficiënten aanzienlijk veranderen.

Gestandaardiseerde residuen verwijzen naar het gestandaardiseerde verschil tussen een voorspelde waarde voor een waarneming en de werkelijke waarde van de waarneming.

Opgemerkt moet worden dat een waarneming een hoge absolute waarde kan hebben voor een gestandaardiseerd residu, maar een lage waarde voor hefboomwerking.

Hoe u een grafiek van residuen versus hefboomwerking interpreteert

Als een punt op deze grafiek buiten de Cook-afstand (de rode stippellijnen) valt, wordt het als een invloedrijke waarneming beschouwd.

Laten we eens kijken naar de eerder getoonde grafiek van residuen versus hefboomwerking:

In het bovenstaande voorbeeld kunnen we zien dat observatie #10 het dichtst bij de Cook-afstandslimiet ligt, maar niet buiten de stippellijn gaat. Dit betekent dat er geen invloedrijke punten zijn in ons regressiemodel.

Stel echter dat we de volgende rest-/hefboomgrafiek hebben:

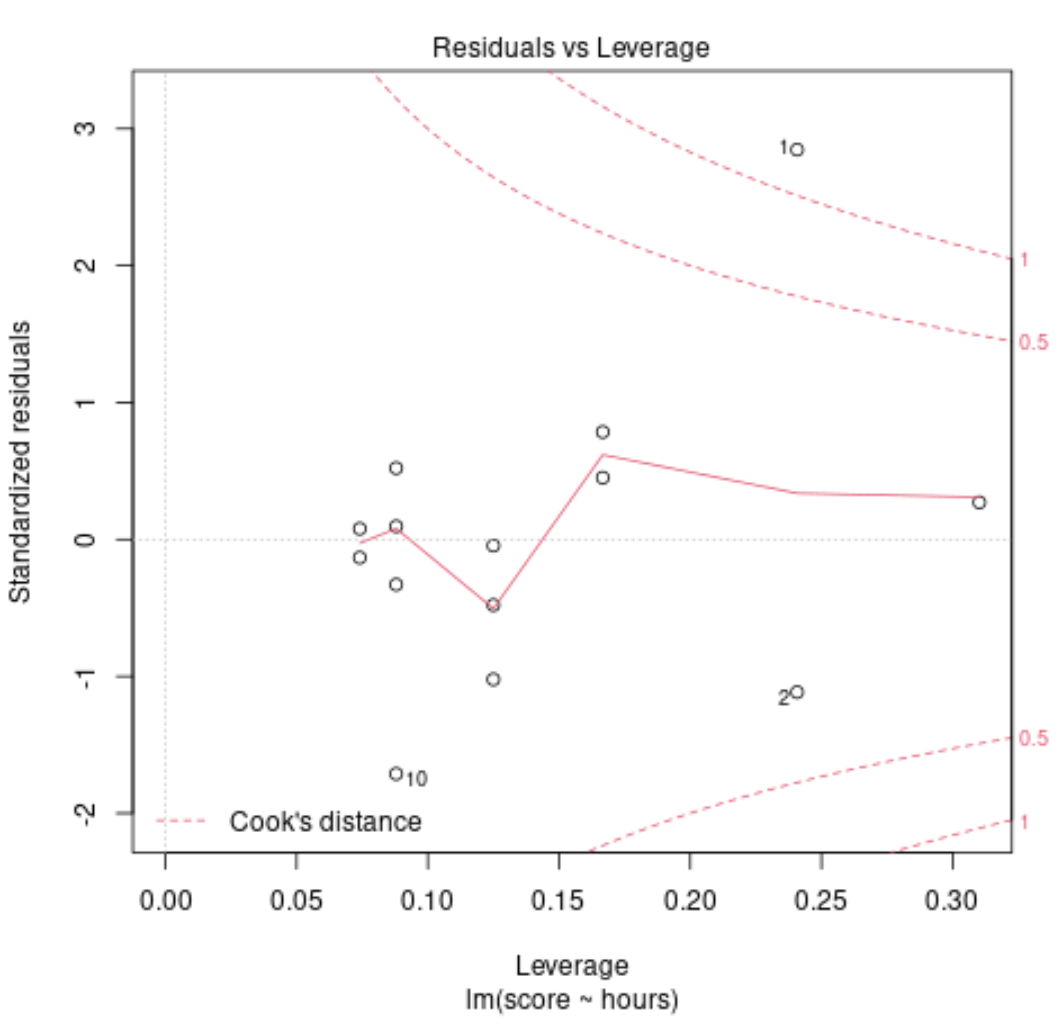
We kunnen zien dat observatie nr. 1 in de rechterbovenhoek zich buiten de rode stippellijnen bevindt. Dit geeft aan dat het een punt van invloed is .

Dit betekent dat als we deze observatie uit onze dataset zouden verwijderen en het regressiemodel opnieuw zouden passen, de modelcoëfficiënten aanzienlijk zouden veranderen.

Hoe om te gaan met invloedrijke observaties

Als u voor een model een grafiek van residuen versus hefboomwerking maakt en ziet dat een of meer waarnemingen als invloedrijk worden geïdentificeerd, kunt u verschillende dingen doen:

1. Controleer of de waarneming geen fout is.

Voordat u actie onderneemt, moet u eerst verifiëren dat invloedrijke waarnemingen niet het resultaat zijn van een gegevensinvoerfout of een andere vreemde gebeurtenis.

2. Probeer een ander regressiemodel toe te passen.

Invloedrijke observaties kunnen erop wijzen dat het door u gespecificeerde model niet goed bij de gegevens past. In dit geval kunt u een polynoomregressiemodel of een niet-lineair model proberen.

3. Verwijder invloedrijke reacties.

Ten slotte kunt u besluiten invloedrijke waarnemingen eenvoudigweg te verwijderen als het door u gespecificeerde model goed bij de gegevens lijkt te passen, met uitzondering van één of twee invloedrijke waarnemingen.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over het gebruik van residuen om de pasvorm van regressiemodellen te evalueren.

Wat zijn residuen in de statistiek?
Wat zijn gestandaardiseerde residuen?
Hoe diagnostische plots in R