Hoe u met de hand een restpad kunt maken

Een residuele plot is een type plot dat de waarden van een voorspellende variabele in een regressiemodel langs de x-as en de waarden van de residuen langs de y-as weergeeft.

Deze plot wordt gebruikt om te evalueren of de residuen van een regressiemodel normaal verdeeld zijn en of ze al dan niet heteroscedasticiteit vertonen.

Het volgende stapsgewijze voorbeeld laat zien hoe u handmatig een residuele plot voor een regressiemodel kunt maken.

Stap 1: Zoek de voorspelde waarden

Stel dat we een regressiemodel willen aanpassen aan de volgende gegevensset:

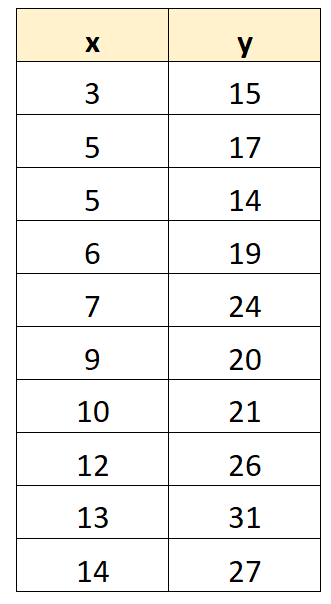
Met behulp van statistische software (zoals Excel, R, Python, SPSS, enz.) kunnen we zien dat het gepaste regressiemodel:

y = 10,4486 + 1,3037(x)

We kunnen dit model vervolgens gebruiken om de waarde van y te voorspellen, gebaseerd op de waarde van x. Als x = 3, voorspellen we bijvoorbeeld dat y zal zijn:

y = 10,4486 + 1,3037(3) = 14,359

We kunnen dit proces herhalen voor elke waarneming in onze dataset:

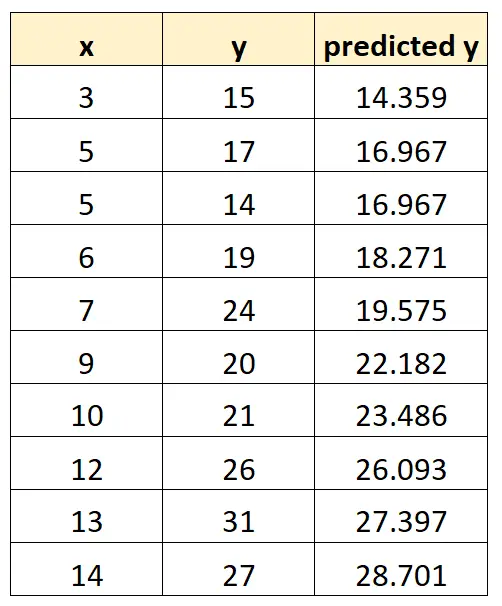
Stap 2: Zoek de residuen

Een residu voor een bepaalde waarneming in onze dataset wordt als volgt berekend:

Residu = waargenomen waarde – voorspelde waarde

Het residu van de eerste waarneming zou bijvoorbeeld als volgt worden berekend:

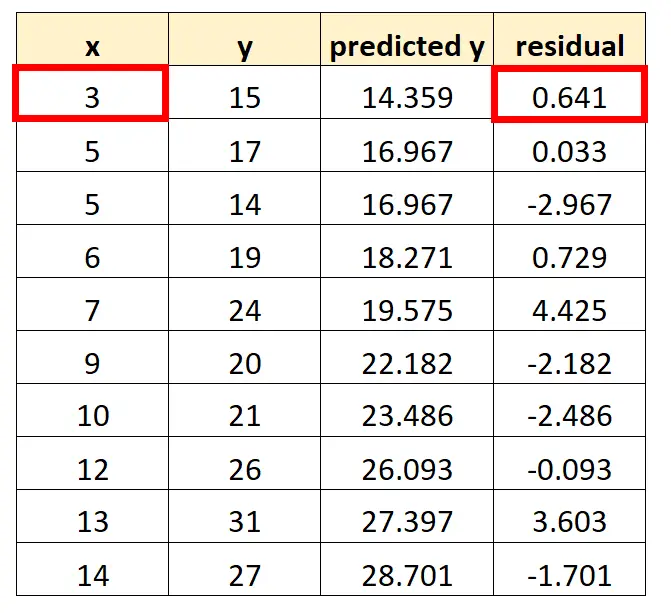
Residu = 15 – 14,359 = 0,641

We kunnen dit proces herhalen voor elke waarneming in onze dataset:

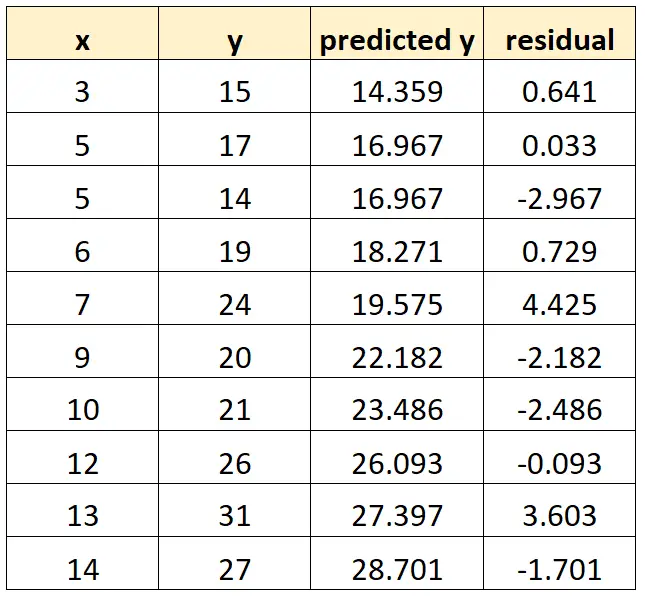
Stap 3: Maak het restplot

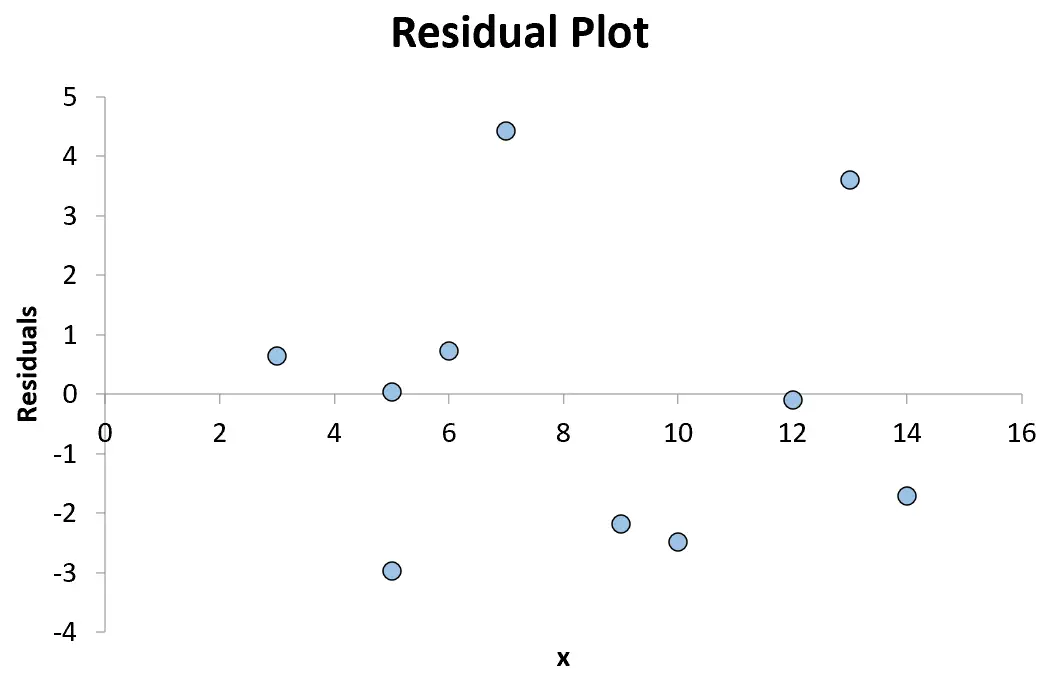
Ten slotte kunnen we een residuele grafiek maken door de x-waarden langs de x-as en de residuen langs de y-as te plaatsen.

Het eerste punt dat we in onze grafiek plaatsen is bijvoorbeeld (3, 0,641)

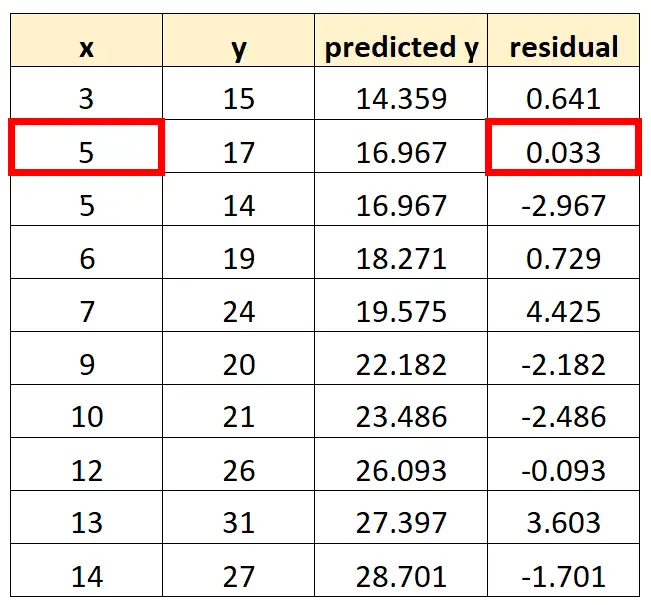
Het volgende punt dat we in onze grafiek zullen plaatsen is (5, 0,033)

We gaan door totdat we alle 10 paarsgewijze combinaties van x-waarden en residuen in de grafiek hebben geplaatst:

Elk punt boven nul in de grafiek vertegenwoordigt een positief residu. Dit betekent dat de waargenomen waarde voor y groter is dan de waarde voorspeld door het regressiemodel.

Elk punt kleiner dan nul vertegenwoordigt een negatief residu. Dit betekent dat de waargenomen waarde voor y lager is dan de waarde voorspeld door het regressiemodel.

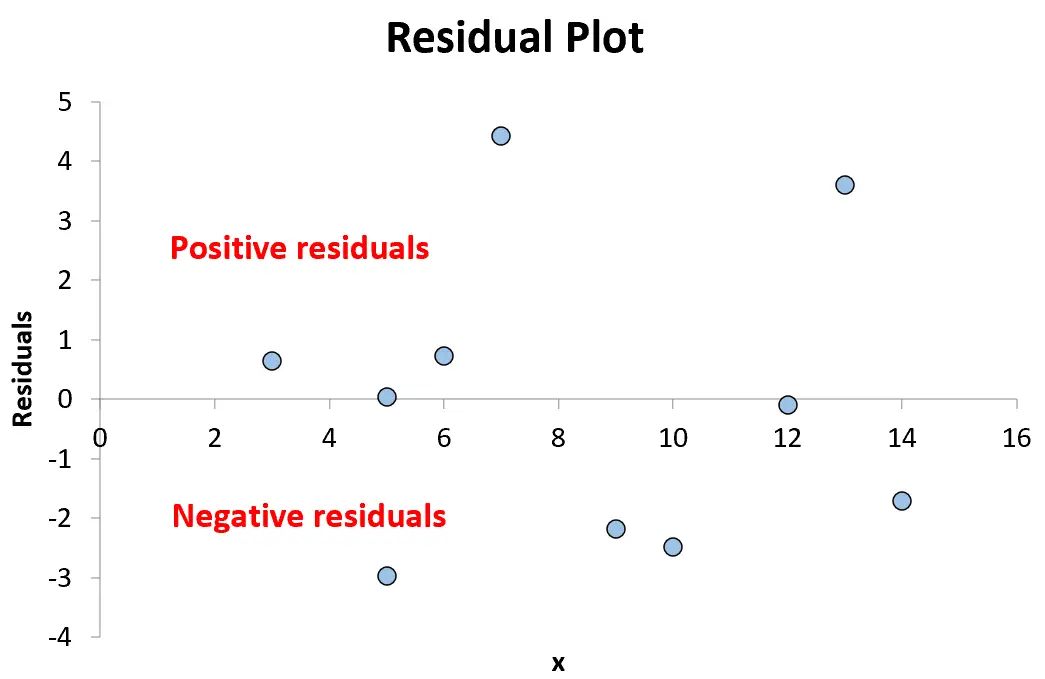
Omdat de punten in de grafiek willekeurig verspreid zijn rond een residu van 0 zonder duidelijk patroon, geeft dit aan dat de relatie tussen x en y lineair is en dat het passend is om een lineair regressiemodel te gebruiken.

En aangezien de residuen niet systematisch toenemen of afnemen naarmate de voorspellende variabele toeneemt, betekent dit dat heteroscedasticiteit geen probleem is met dit regressiemodel.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u restplots kunt maken met behulp van verschillende statistische software:

Hoe maak je een resterend plot op een TI-84-rekenmachine?
Hoe u een restplot in Excel maakt
Hoe maak je een restplot in R
Hoe u een restplot maakt in Python