Wat is het resterende gat? (definitie & #038; voorbeeld)

Residuele variantie (ook wel „onverklaarde variantie“ genoemd) verwijst naar de variantie in een model die niet kan worden verklaard door de modelvariabelen.

Hoe hoger de residuele variantie van een model, hoe minder het model de variatie in de gegevens kan verklaren.

Residuele variantie komt voor in de resultaten van twee verschillende statistische modellen:

1. ANOVA: gebruikt om de gemiddelden van drie of meer onafhankelijke groepen te vergelijken.

2. Regressie: gebruikt om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te kwantificeren.

De volgende voorbeelden laten zien hoe u de resterende variantie in elk van deze methoden kunt interpreteren.

Resterende variantie in ANOVA-modellen

Elke keer dat we een ANOVA-model (“variantieanalyse”) passen, krijgen we een ANOVA-tabel die er als volgt uitziet:

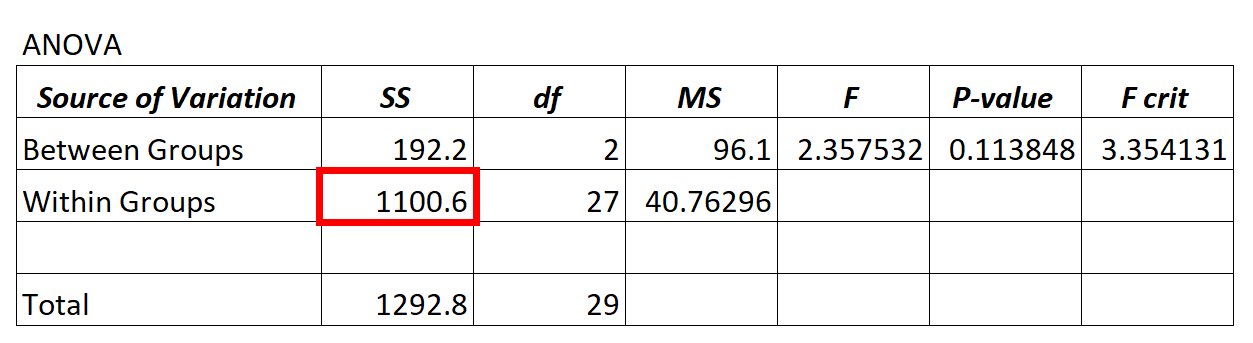
De resterende variantiewaarde van het ANOVA-model is te vinden in de SS-kolom (“som van de kwadraten”) voor variatie binnen de groep .

Deze waarde wordt ook wel de som van de kwadratische fouten genoemd en wordt berekend met behulp van de volgende formule:

Σ _{( Xij} – Xj ) ²

Goud:

• Σ : een Grieks symbool dat “som” betekent
• X _ij : de ^ide waarneming van groep j
• Xj _: het gemiddelde van groep j

In het bovenstaande ANOVA-model zien we dat de residuele variantie 1100,6 is.

Om te bepalen of deze residuele variantie „hoog“ is, kunnen we de gemiddelde som van de kwadraten voor binnen groepen en de gemiddelde som van de kwadraten voor tussen groepen berekenen en de verhouding tussen de twee vinden, die de totale F-waarde in de ANOVA-tabel oplevert.

• F = MS _{komt binnen} / MS _{komt binnen}
• F = 96,1 / 40,76296
• F = 2,357

De F-waarde in de bovenstaande ANOVA-tabel is 2,357 en de overeenkomstige p-waarde is 0,113848. Omdat deze p-waarde niet kleiner is dan α = 0,05, hebben we niet voldoende bewijs om de nulhypothese te verwerpen.

Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat het gemiddelde verschil tussen de groepen die we vergelijken significant verschillend is.

Dit vertelt ons dat de resterende variantie van het ANOVA-model hoog is vergeleken met de variatie die het model feitelijk kan verklaren.

Residuele variantie in regressiemodellen

In een regressiemodel wordt de residuele variantie gedefinieerd als de som van de kwadraten van de verschillen tussen de voorspelde datapunten en de waargenomen datapunten.

Het wordt als volgt berekend:

Σ(ŷ _ik – y _ik ) ²

Goud:

• Σ : een Grieks symbool dat “som” betekent
• ŷ _i : De voorspelde gegevenspunten
• y _i : De waargenomen gegevenspunten

Wanneer we een regressiemodel passen, krijgen we meestal een resultaat dat er als volgt uitziet:

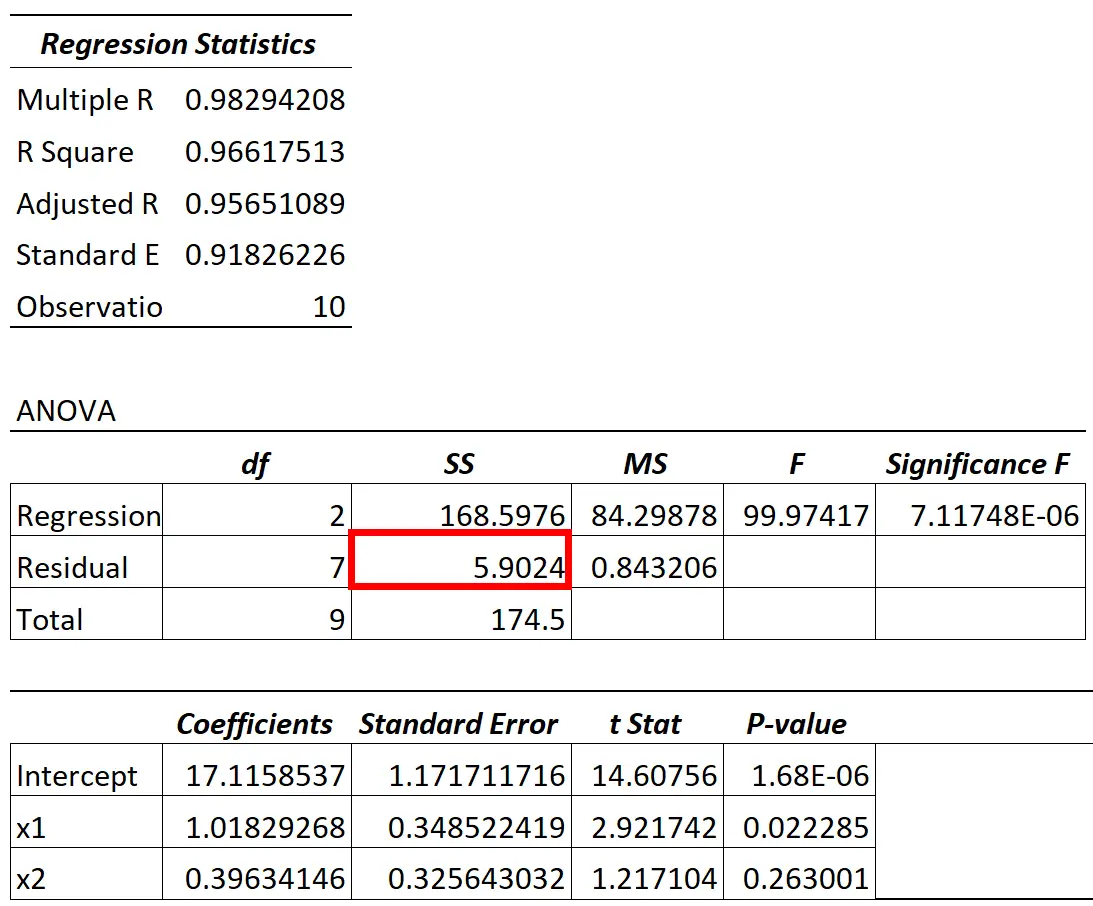
De resterende variantiewaarde van het ANOVA-model is te vinden in de SS-kolom (“som van de kwadraten”) voor resterende variatie.

De verhouding tussen de resterende variatie en de totale variatie in het model vertelt ons het percentage variatie in de responsvariabele dat niet kan worden verklaard door de voorspellende variabelen in het model.

In de bovenstaande tabel berekenen we dit percentage bijvoorbeeld als volgt:

• Onverklaarde variatie = SS-residu / SS-totaal
• Onverklaarde variatie = 5,9024 / 174,5
• Onverklaarde variatie = 0,0338

Deze waarde kan ook worden berekend met de volgende formule:

• Onverklaarde variatie = 1 – R ²
• Onverklaarde variatie = 1 – 0,96617
• Onverklaarde variatie = 0,0338

De R-kwadraatwaarde van het model vertelt ons het percentage variatie in de responsvariabele dat kan worden verklaard door de voorspellende variabele.

Dus hoe lager de onverklaarde variatie, hoe beter een model in staat is de voorspellende variabelen te gebruiken om de variatie in de responsvariabele te verklaren.

Aanvullende bronnen

Wat is een goede R-kwadraatwaarde?
Hoe R-kwadraat te berekenen in Excel
Hoe R-kwadraat in R te berekenen