Robuuste regressie uitvoeren in r (stap voor stap)

Robuuste regressie is een methode die we kunnen gebruiken als alternatief voor de gewone kleinste kwadratenregressie als er uitbijters of invloedrijke waarnemingen voorkomen in de dataset waarmee we werken.

Om robuuste regressie in R uit te voeren, kunnen we de functie rlm() uit het MASS- pakket gebruiken, die de volgende syntaxis gebruikt:

Het volgende stapsgewijze voorbeeld laat zien hoe u robuuste regressie in R kunt uitvoeren voor een bepaalde gegevensset.

Stap 1: Creëer de gegevens

Laten we eerst een nep-dataset maken om mee te werken:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Stap 2: Voer gewone kleinste-kwadratenregressie uit

Laten we vervolgens een gewoon regressiemodel met de kleinste kwadraten toepassen en een grafiek van de gestandaardiseerde residuen maken.

In de praktijk beschouwen we vaak elk gestandaardiseerd residu waarvan de absolute waarde groter is dan 3 als een uitbijter.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

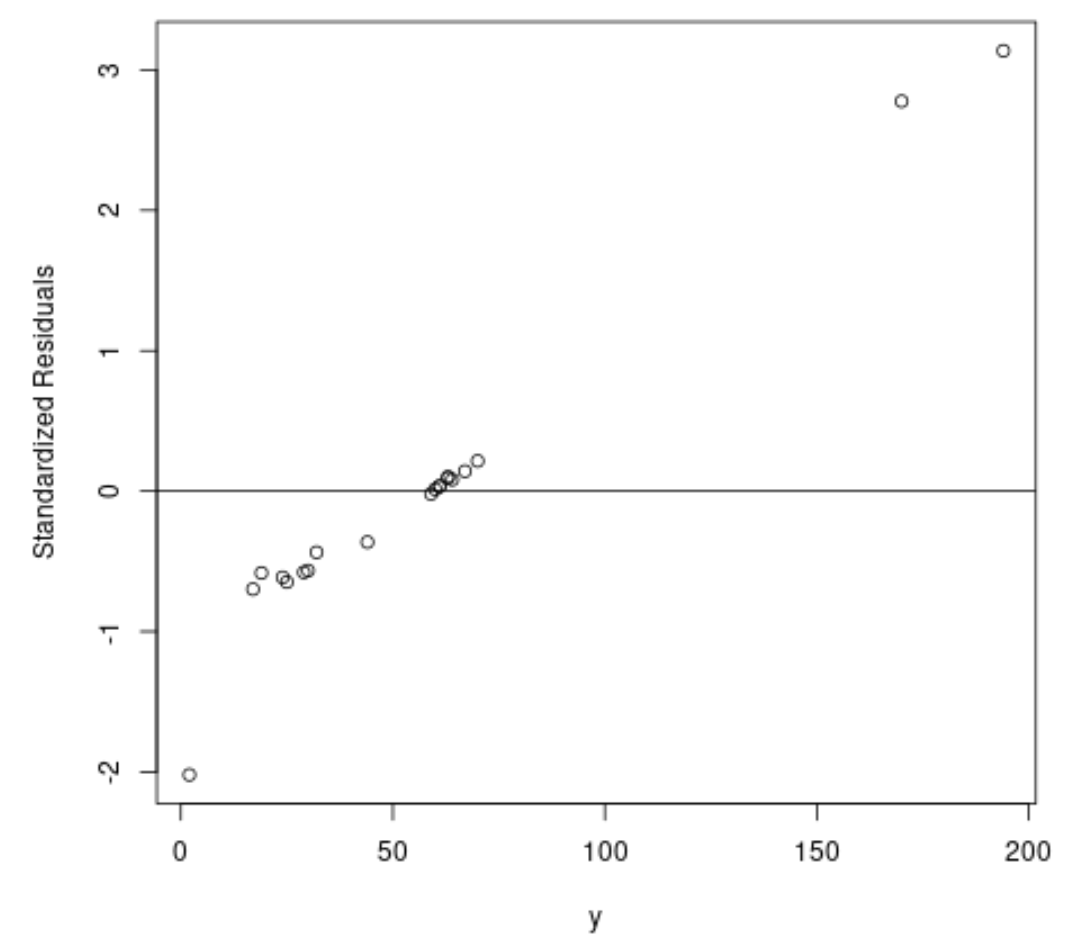
Uit de grafiek kunnen we zien dat er twee waarnemingen zijn met gestandaardiseerde residuen rond de 3.

Dit geeft aan dat er twee potentiële uitschieters in de dataset zitten en dat we daarom wellicht kunnen profiteren van robuuste regressie.

Stap 3: Voer robuuste regressie uit

Laten we vervolgens de functie rlm() gebruiken om een robuust regressiemodel in te passen:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Om te bepalen of dit robuuste regressiemodel beter aansluit bij de gegevens vergeleken met het OLS-model, kunnen we de resterende standaardfout van elk model berekenen.

De residuele standaardfout (RSE) is een manier om de standaardafwijking van de residuen in een regressiemodel te meten. Hoe lager de MVO-waarde, hoe beter een model bij de data past.

De volgende code laat zien hoe u de RSE voor elk model kunt berekenen:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

We kunnen zien dat de RSE van het robuuste regressiemodel veel lager is dan die van het gewone regressiemodel met de kleinste kwadraten, wat ons vertelt dat het robuuste regressiemodel beter aansluit bij de gegevens.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe polynomiale regressie uit te voeren in R