Hoe u robuuste standaardfouten kunt gebruiken bij regressie in stata

Meervoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen meerdere verklarende variabelen en een responsvariabele te begrijpen.

Helaas staat een probleem dat vaak voorkomt bij regressie bekend als heteroscedasticiteit , waarbij er een systematische verandering is in de variantie van de residuen over een reeks gemeten waarden.

Dit leidt tot een toename van de variantie van de schattingen van de regressiecoëfficiënten, maar het regressiemodel houdt hier geen rekening mee. Dit maakt het veel waarschijnlijker dat een regressiemodel zal beweren dat een term in het model statistisch significant is, terwijl dit in werkelijkheid niet het geval is.

Eén manier om dit probleem te verklaren is het gebruik van robuuste standaardfouten , die „robuuster“ zijn voor het probleem van heteroskedasticiteit en de neiging hebben een nauwkeuriger maatstaf te bieden voor de werkelijke standaardfout van een regressiecoëfficiënt.

In deze tutorial wordt uitgelegd hoe u robuuste standaardfouten kunt gebruiken bij regressieanalyse in Stata.

Voorbeeld: Robuuste standaardfouten in Stata

We zullen de automatisch geïntegreerde Stata-dataset gebruiken om te illustreren hoe robuuste standaardfouten bij regressie kunnen worden gebruikt.

Stap 1: Gegevens laden en weergeven.

Gebruik eerst de volgende opdracht om de gegevens te laden:

automatisch gebruik van het systeem

Geef vervolgens de onbewerkte gegevens weer met behulp van de volgende opdracht:

br

Stap 2: Voer meervoudige lineaire regressie uit zonder robuuste standaardfouten.

Vervolgens voeren we de volgende opdracht in om een meervoudige lineaire regressie uit te voeren, waarbij prijs als antwoordvariabele en mpg en gewicht als verklarende variabelen worden gebruikt:

regressie prijs mpg gewicht

Stap 3: Voer meervoudige lineaire regressie uit met behulp van robuuste standaardfouten.

We zullen nu exact dezelfde meervoudige lineaire regressie uitvoeren, maar deze keer zullen we de opdracht vce(robust) gebruiken, zodat Stata weet hoe hij robuuste standaardfouten moet gebruiken:

regressieprijs mpg gewicht, vce (robuust)

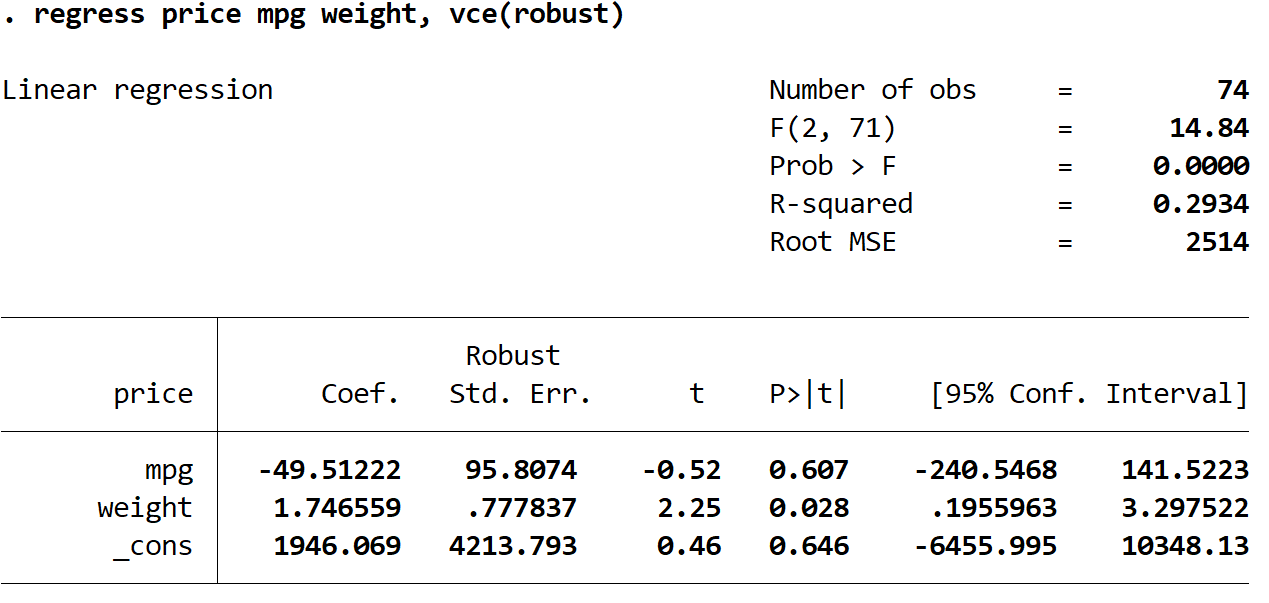
Er zijn hier een paar interessante dingen om op te merken:

1. De coëfficiëntenschattingen bleven hetzelfde . Wanneer we robuuste standaardfouten gebruiken, veranderen de schattingen van de coëfficiënten helemaal niet. Merk op dat de coëfficiëntschattingen voor mpg, gewicht en constante als volgt zijn voor beide regressies:

• mpg: -49,51222
• gewicht: 1,746559
• _tegen: 1946.069

2. Standaardfouten zijn veranderd . Merk op dat wanneer we robuuste standaardfouten gebruikten, de standaardfouten voor elk van de coëfficiëntschattingen toenamen.

Opmerking: In de meeste gevallen zullen de robuuste standaardfouten groter zijn dan de normale standaardfouten, maar in zeldzame gevallen is het mogelijk dat de robuuste standaardfouten feitelijk kleiner zullen zijn.

3. De teststatistiek van elke coëfficiënt is veranderd. Merk op dat de absolute waarde van elke teststatistiek , t , is afgenomen. In feite wordt de teststatistiek berekend als de geschatte coëfficiënt gedeeld door de standaardfout. Dus hoe groter de standaardfout, hoe kleiner de absolute waarde van de teststatistiek.

4. De p-waarden zijn veranderd . Merk op dat de p-waarden voor elke variabele ook zijn toegenomen. Dit komt omdat kleinere teststatistieken geassocieerd zijn met grotere p-waarden.

Hoewel de p-waarden voor onze coëfficiënten zijn veranderd, is de mpg- variabele nog steeds niet statistisch significant bij α = 0,05 en is het variabele gewicht nog steeds statistisch significant bij α = 0,05.