Hoe u de root mean square error (rmse) in excel kunt berekenen

In de statistiek is regressieanalyse een techniek die we gebruiken om de relatie tussen een voorspellende variabele, x, en een responsvariabele, y, te begrijpen.

Wanneer we regressieanalyse uitvoeren, krijgen we een model dat ons de voorspelde waarde van de responsvariabele vertelt op basis van de waarde van de voorspellende variabele.

Eén manier om te beoordelen hoe goed ons model bij een bepaalde dataset past, is door de gemiddelde kwadratische fout te berekenen, een metriek die ons vertelt hoe ver onze voorspelde waarden gemiddeld verwijderd zijn van onze waargenomen waarden.

De formule voor het vinden van de gemiddelde kwadratische fout, beter bekend als RMSE , is:

RMSE = √[ Σ(P _ik – O _ik ) ² / n ]

Goud:

• Σ is een mooi symbool dat ‘som’ betekent
• _Pi is de voorspelde waarde voor de ^i- de waarneming in de dataset
• O _i is de waargenomen waarde voor de ^i- de waarneming in de dataset
• n is de steekproefomvang

Technische opmerkingen :

• De gemiddelde kwadratische fout kan worden berekend voor elk type model dat voorspelde waarden oplevert, die vervolgens kunnen worden vergeleken met de waargenomen waarden van een dataset.
• De gemiddelde kwadratische fout wordt ook wel de gemiddelde kwadratische afwijking genoemd, vaak afgekort als RMSD.

Laten we vervolgens een voorbeeld bekijken van hoe u de gemiddelde kwadratische fout in Excel kunt berekenen.

Hoe de gemiddelde vierkante fout in Excel te berekenen

Er is geen ingebouwde functie om RMSE in Excel te berekenen, maar we kunnen het vrij eenvoudig berekenen met een enkele formule. We zullen laten zien hoe u de RMSE voor twee verschillende scenario’s kunt berekenen.

Scenario 1

In een scenario kunt u één kolom hebben met de voorspelde waarden uit uw model en een andere kolom met de waargenomen waarden. De onderstaande afbeelding toont een voorbeeld van dit scenario:

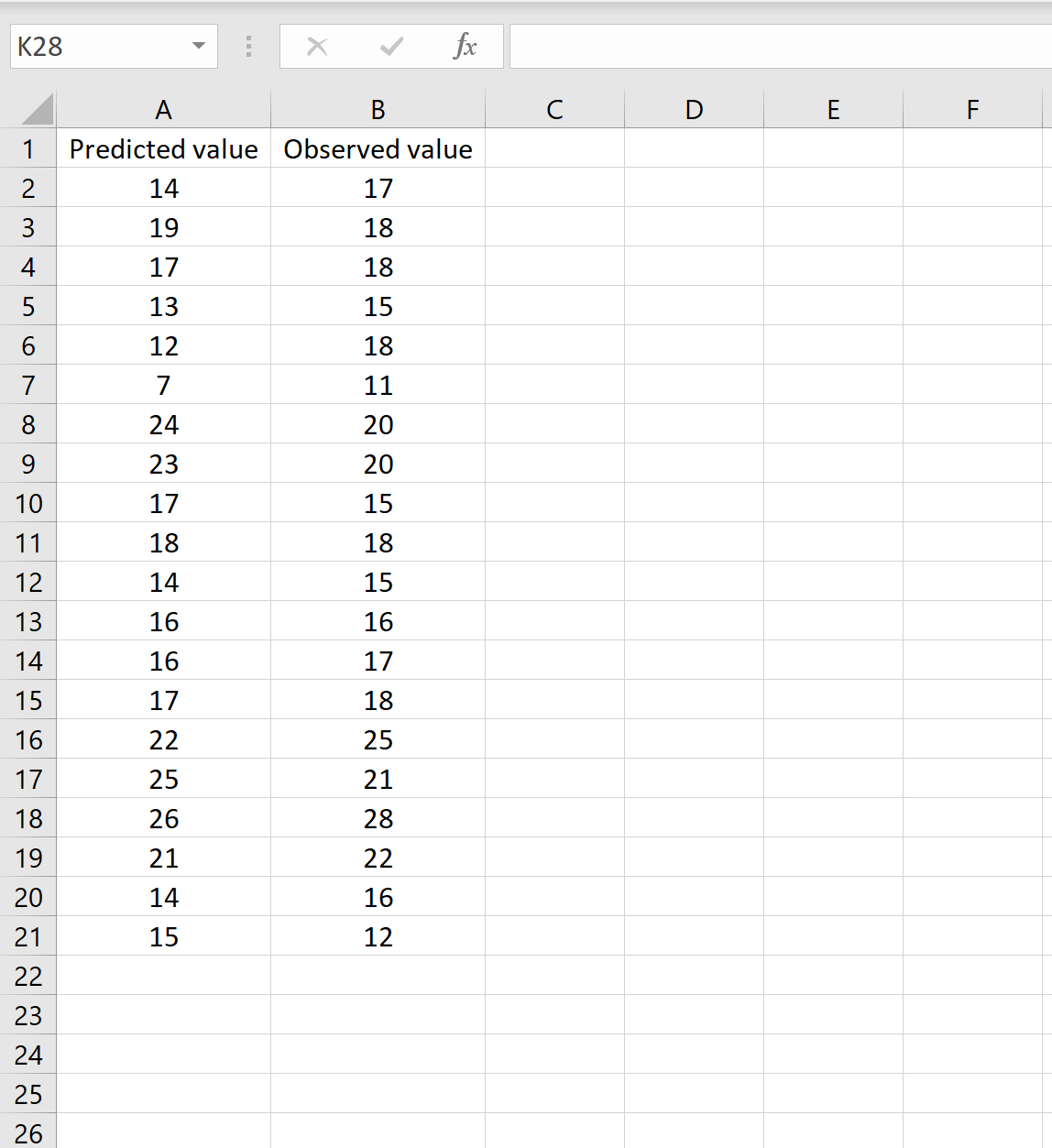
Als dat het geval is, kunt u de RMSE berekenen door de volgende formule in een willekeurige cel te typen en vervolgens op CTRL+SHIFT+ENTER te klikken:

=SQRT(SUMSQ(A2:A21-B2:B21) / AANTAL(A2:A21))

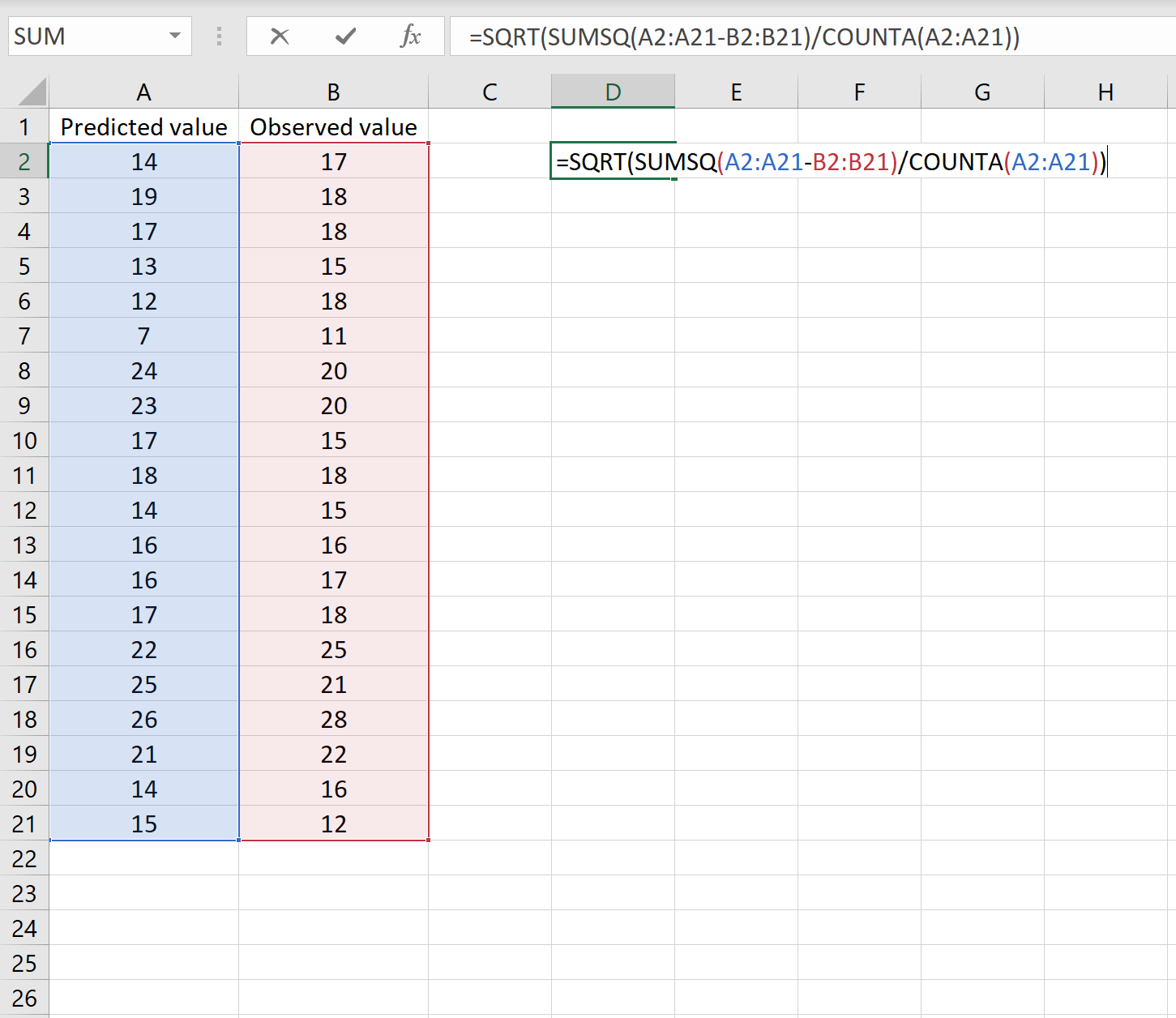
Dit vertelt ons dat de gemiddelde kwadratische fout 2,6646 is.

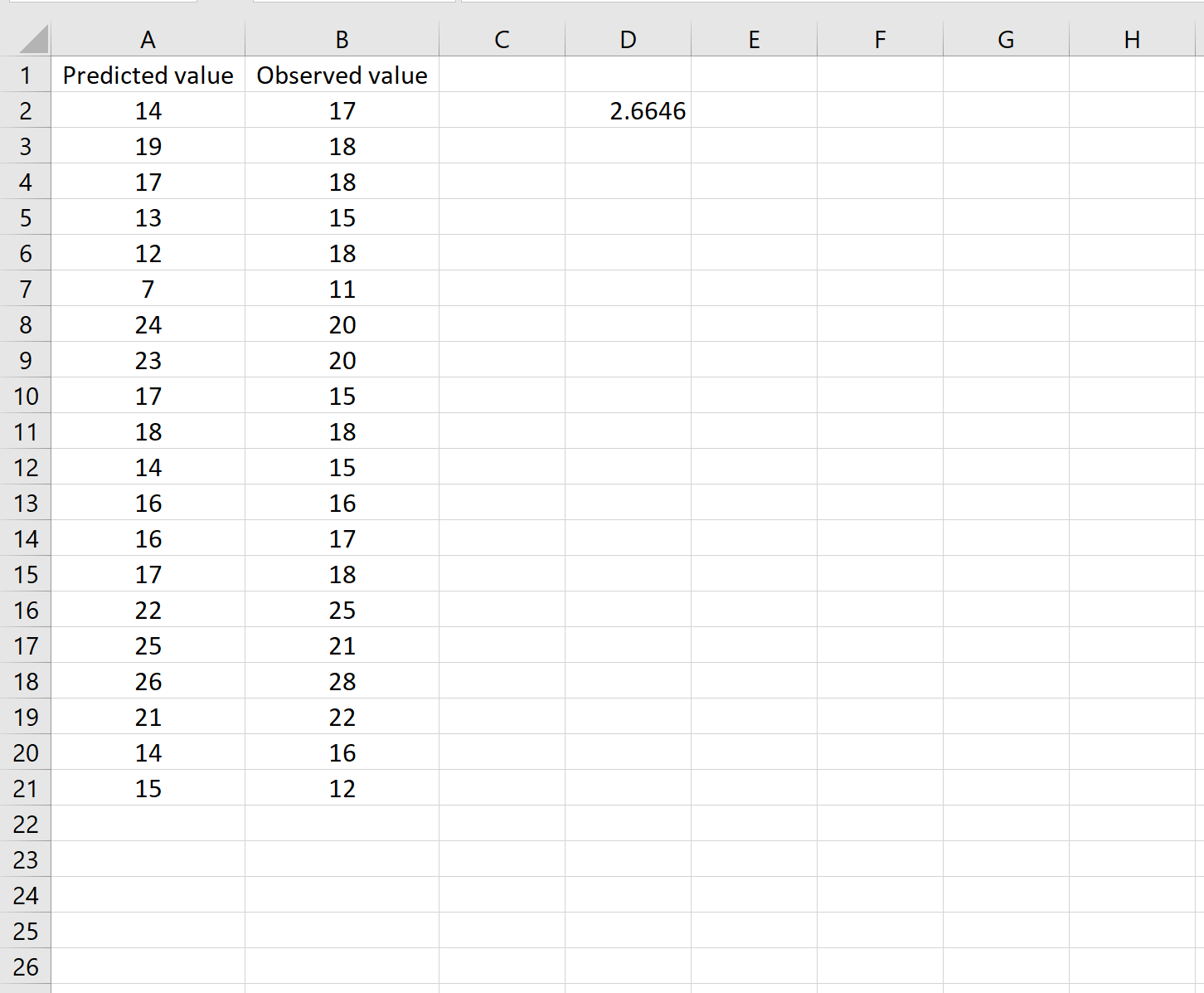
De formule lijkt misschien een beetje lastig, maar als je hem eenmaal hebt opgesplitst, is hij logisch:

= SQRT( SUMSQ(A2:A21-B2:B21) / AANTAL(A2:A21) )

• Eerst berekenen we de som van de kwadraten van de verschillen tussen de voorspelde en waargenomen waarden met behulp van de functie SUMSQ() .
• Vervolgens delen we door de steekproefomvang van de gegevensset met behulp van COUNTA() , dat het aantal cellen in een bereik telt dat niet leeg is.
• Ten slotte nemen we de vierkantswortel van de gehele berekening met behulp van de functie SQRT() .

Scenario 2

In een ander scenario hebt u mogelijk de verschillen tussen voorspelde en waargenomen waarden al berekend. In dit geval heeft u slechts één kolom waarin de verschillen worden weergegeven.

De onderstaande afbeelding toont een voorbeeld van dit scenario. In kolom A worden de voorspelde waarden weergegeven, in kolom B de waargenomen waarden en in kolom D het verschil tussen de voorspelde en waargenomen waarden:

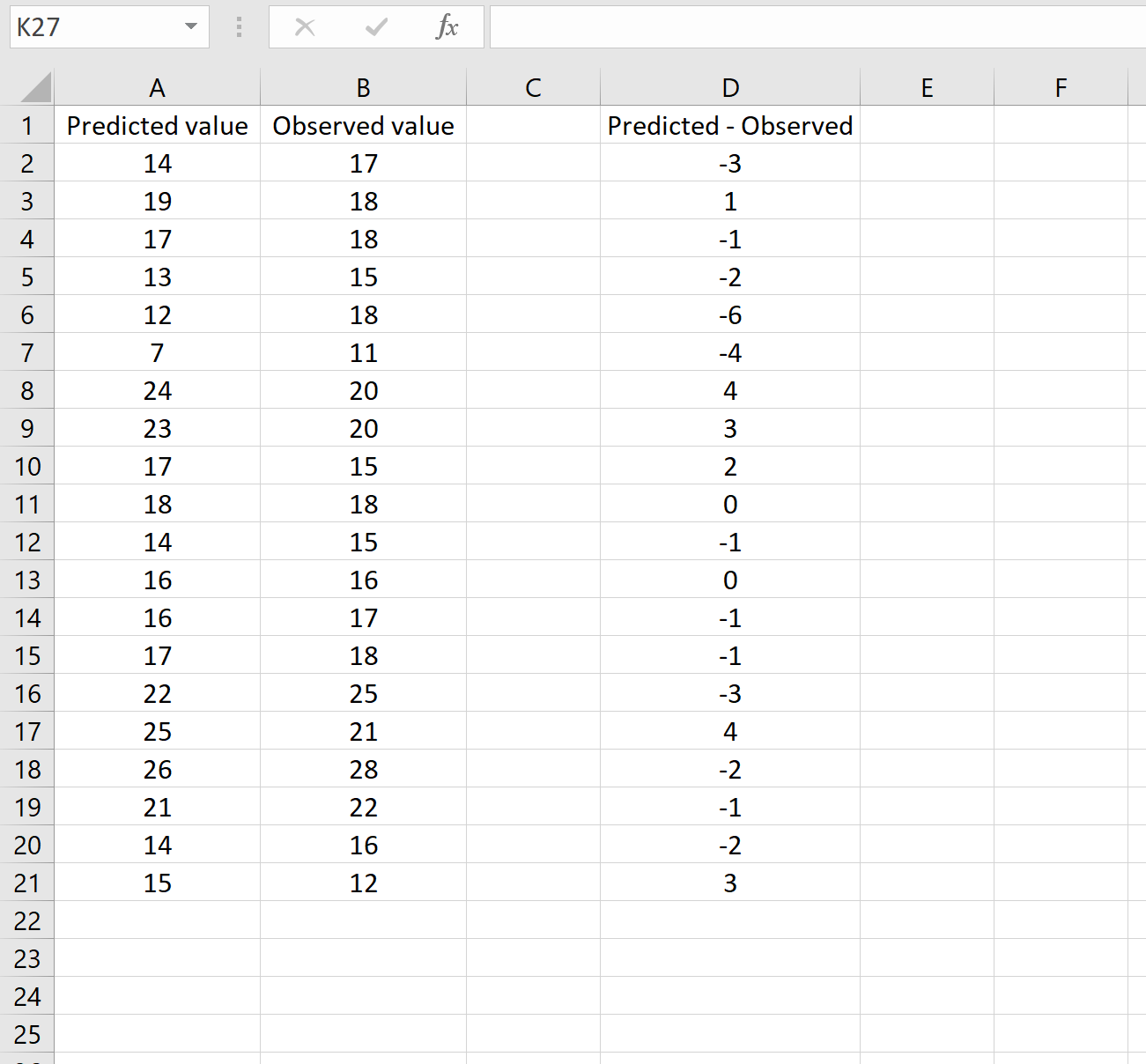
Als dat het geval is, kunt u de RMSE berekenen door de volgende formule in een willekeurige cel te typen en vervolgens op CTRL+SHIFT+ENTER te klikken:

=SQRT(SUMSQ(D2:D21) / AANTAL(D2:D21))

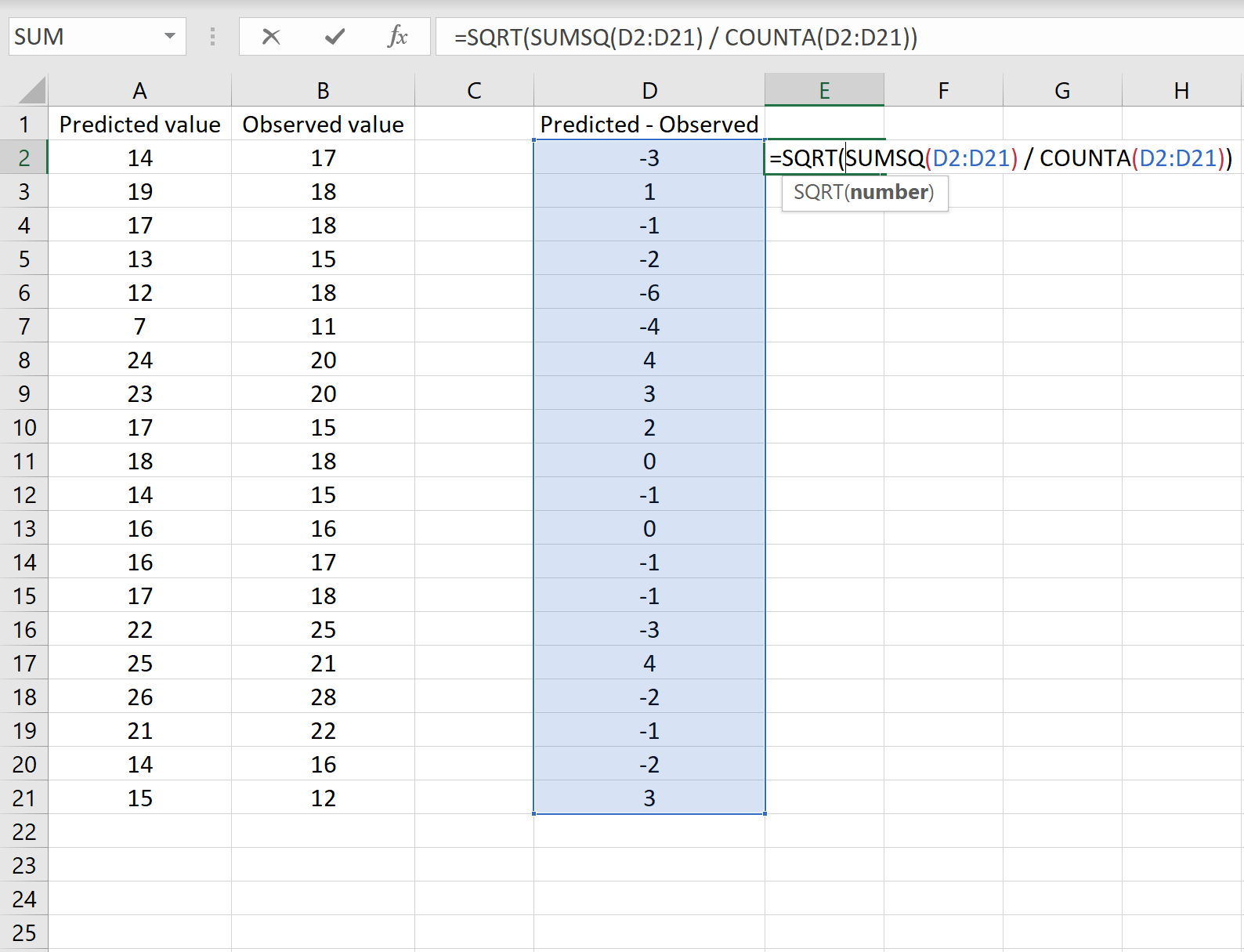
Dit vertelt ons dat de gemiddelde kwadratische fout 2,6646 is, wat overeenkomt met het resultaat dat in het eerste scenario is verkregen. Dit bevestigt dat deze twee benaderingen voor het berekenen van RMSE gelijkwaardig zijn.

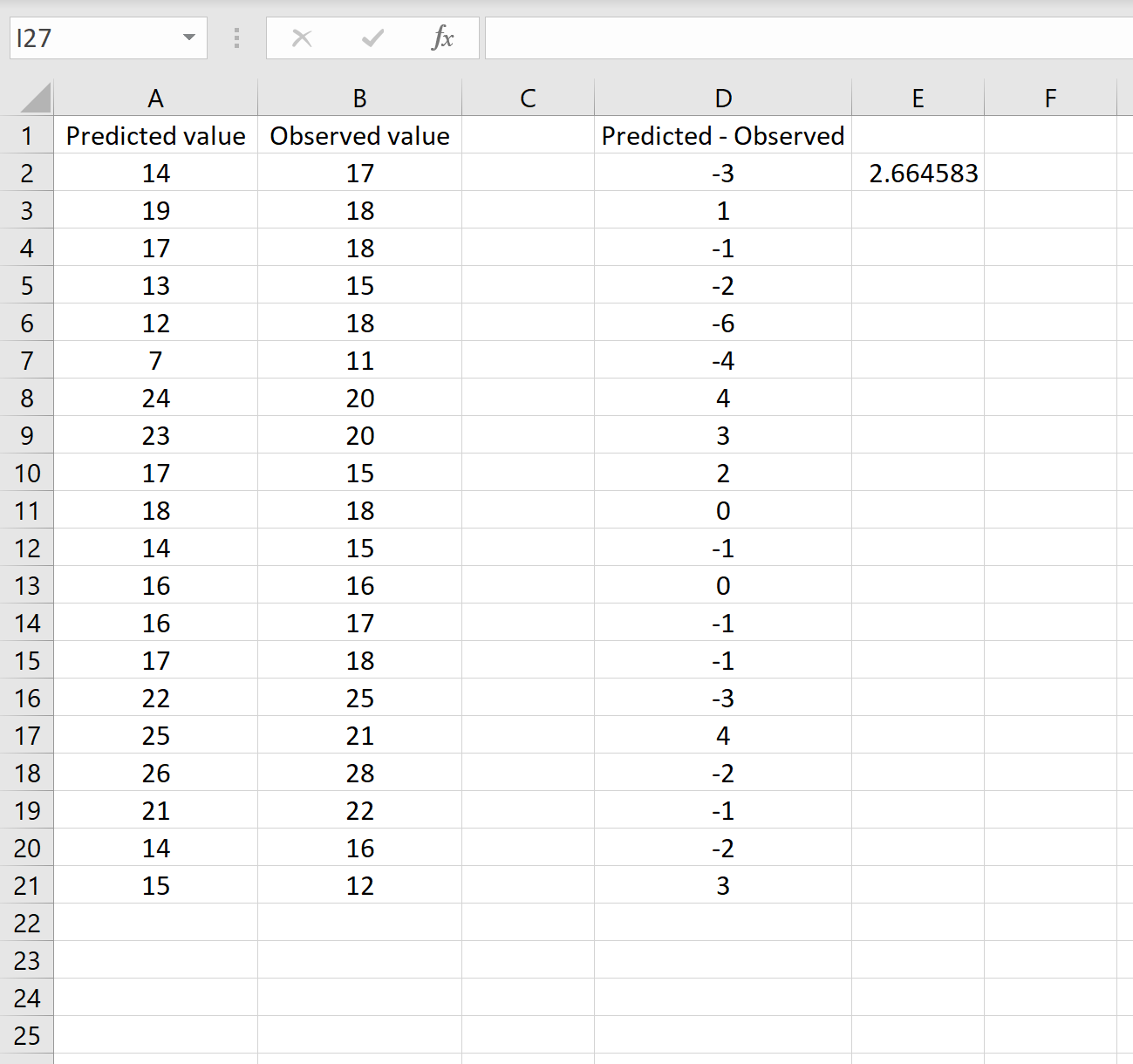
De formule die we in dit scenario gebruikten, verschilt slechts in geringe mate van wat we in het vorige scenario gebruikten:

= SQRT( SOM.Q(D2:D21) / AANTAL(D2:D21) )

• Omdat we de verschillen tussen de voorspelde en waargenomen waarden in kolom D al hebben berekend, kunnen we de som van de gekwadrateerde verschillen berekenen met behulp van de functie SUMSQ().   functie met alleen de waarden uit kolom D.
• Vervolgens delen we door de steekproefomvang van de gegevensset met behulp van COUNTA() , dat het aantal cellen in een bereik telt dat niet leeg is.
• Ten slotte nemen we de vierkantswortel van de gehele berekening met behulp van de functie SQRT() .

Hoe de RMSE te interpreteren

Zoals eerder vermeld is RMSE een nuttige manier om te zien hoe goed een regressiemodel (of een ander model dat voorspelde waarden produceert) in een dataset kan „passen“.

Hoe groter de RMSE, hoe groter het verschil tussen de voorspelde en waargenomen waarden, wat betekent dat hoe slechter het regressiemodel bij de gegevens past. Omgekeerd geldt: hoe kleiner de RMSE, hoe beter het model bij de gegevens kan passen.

Het kan bijzonder nuttig zijn om de RMSE van twee verschillende modellen te vergelijken om te zien welk model het beste bij de gegevens past.

Voor meer tutorials in Excel kunt u onze Excel-handleidingenpagina raadplegen, waarop alle Excel-tutorials over statistieken staan vermeld.