Hoe u een roc-curve in stata maakt en interpreteert

Logistische regressie is een statistische methode die we gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is. Om te evalueren hoe goed een logistisch regressiemodel bij een dataset past, kunnen we naar de volgende twee statistieken kijken:

• Gevoeligheid: de kans dat het model een positief resultaat voorspelt voor een waarneming terwijl het resultaat daadwerkelijk positief is.
• Specificiteit: de kans dat het model een negatief resultaat voorspelt voor een waarneming terwijl het resultaat feitelijk negatief is.

Een eenvoudige manier om deze twee statistieken te visualiseren is door een ROC-curve te maken, een grafiek die de gevoeligheid en specificiteit van een logistisch regressiemodel weergeeft.

In deze tutorial wordt uitgelegd hoe u een ROC-curve in Stata maakt en interpreteert.

Voorbeeld: ROC-curve in Stata

Voor dit voorbeeld gebruiken we een dataset genaamd lbw , die de volgende variabelen bevat voor 189 moeders:

• laag – of de baby al dan niet een laag geboortegewicht heeft. 1 = ja, 0 = nee.
• leeftijd – leeftijd van de moeder.
• roken – ongeacht of de moeder tijdens de zwangerschap rookte of niet. 1 = ja, 0 = nee.

We zullen een logistisch regressiemodel op de gegevens aansluiten, waarbij we leeftijd en roken gebruiken als verklarende variabelen en een laag geboortegewicht als responsvariabele. Vervolgens zullen we een ROC-curve maken om te analyseren hoe goed het model bij de gegevens past.

Stap 1: Gegevens laden en weergeven.

Laad de gegevens met behulp van de volgende opdracht:

gebruik https://www.stata-press.com/data/r13/lbw

Krijg snel inzicht in de dataset met behulp van de volgende opdracht:

samenvatten

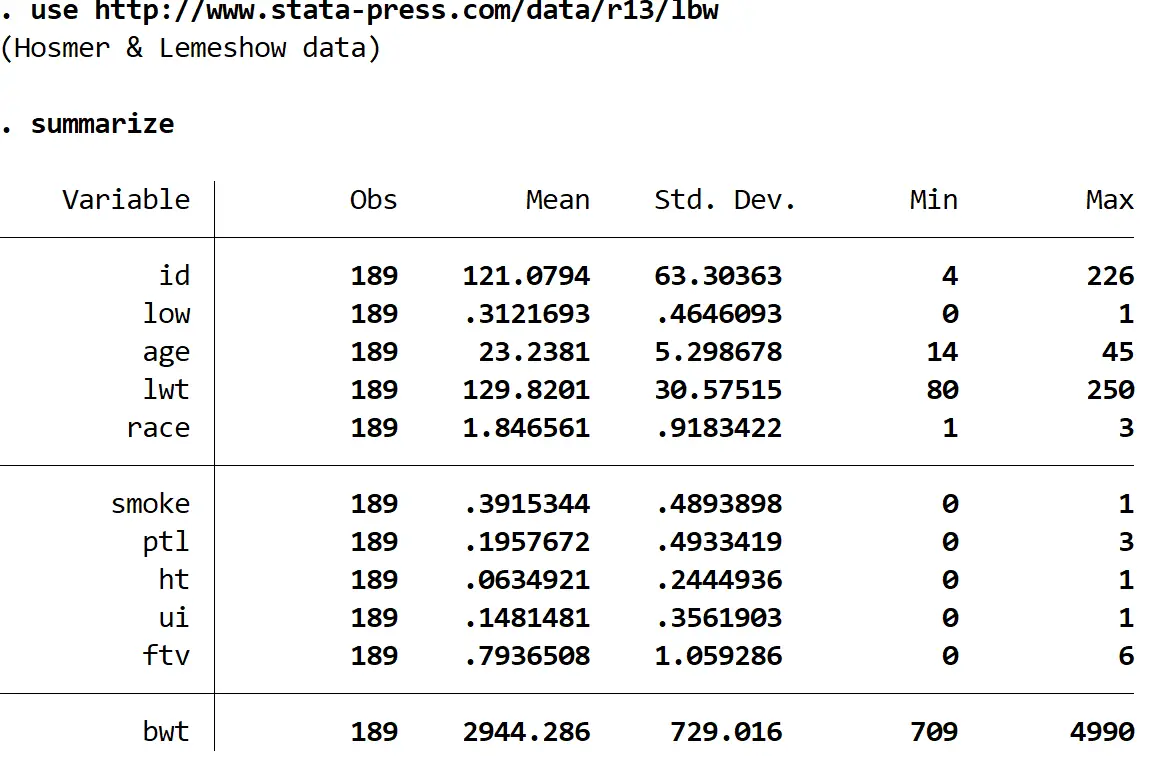
Er zijn elf verschillende variabelen in de dataset, maar de enige drie waarin we geïnteresseerd zijn, zijn laag niveau, leeftijd en roken.

Stap 2: Pas het logistische regressiemodel aan.

Gebruik de volgende opdracht om het logistieke regressiemodel aan te passen:

rooklogit op lage leeftijd

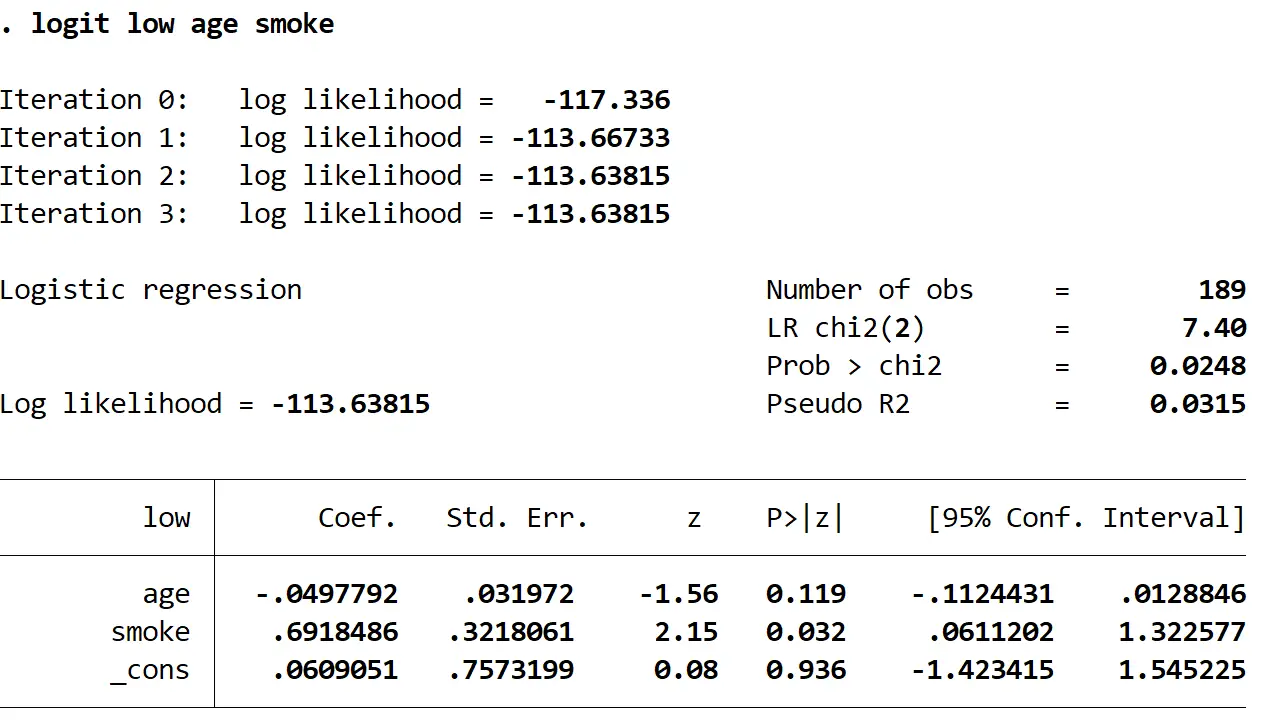
Stap 3: Creëer de ROC-curve.

We kunnen de ROC-curve voor het model maken met behulp van de volgende opdracht:

lroc

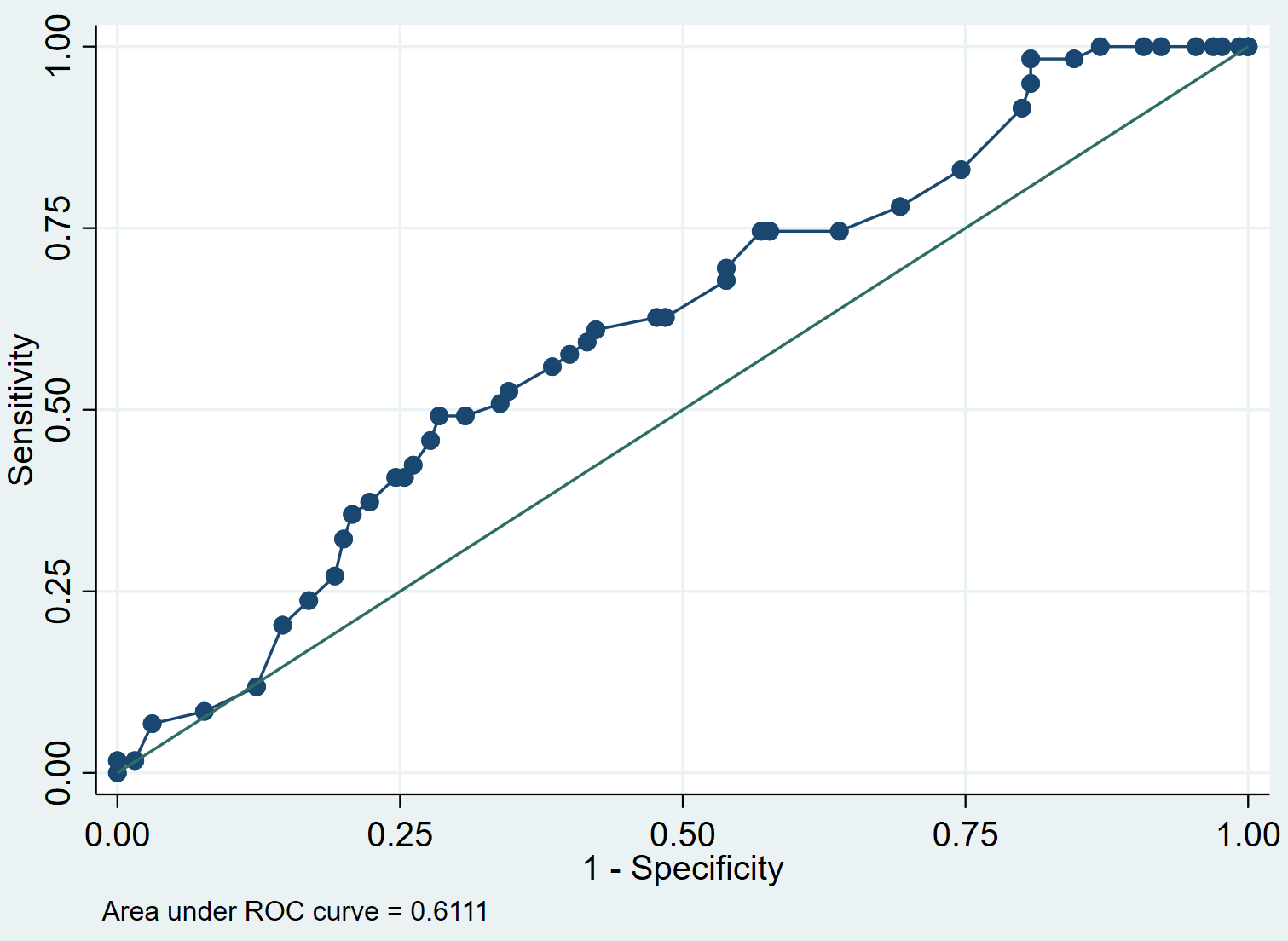
Stap 4: Interpreteer de ROC-curve.

Wanneer we een logistisch regressiemodel passen, kan dit worden gebruikt om de waarschijnlijkheid te berekenen dat een bepaalde waarneming een positief resultaat zal hebben, op basis van de waarden van de voorspellende variabelen.

Om te bepalen of een waarneming als positief moet worden geclassificeerd, kunnen we een zodanige drempel kiezen dat waarnemingen met een aangepaste waarschijnlijkheid boven de drempel als positief worden geclassificeerd en alle waarnemingen met een aangepaste waarschijnlijkheid onder de drempel als negatief worden geclassificeerd. .

Stel dat we bijvoorbeeld een drempelwaarde van 0,5 kiezen. Dit betekent dat elke waarneming met een aangepaste waarschijnlijkheid groter dan 0,5 een positief resultaat zal hebben, terwijl elke waarneming met een aangepaste waarschijnlijkheid kleiner dan of gelijk aan 0,5 een negatief resultaat zal hebben.

De ROC-curve toont ons de gevoeligheidswaarden versus specificiteit 1 terwijl de drempelwaarde verandert van 0 naar 1. Een model met hoge gevoeligheid en specificiteit zal een ROC-curve hebben die de linkerbovenhoek van de plot omhelst. Een model met een lage gevoeligheid en lage specificiteit zal een curve hebben die dichtbij de diagonaal van 45 graden ligt.

De AUC (area under curve) geeft ons een idee van het vermogen van het model om onderscheid te maken tussen positieve en negatieve resultaten. De AUC kan variëren van 0 tot 1. Hoe hoger de AUC, hoe beter het model de resultaten correct classificeert. In ons voorbeeld kunnen we zien dat de AUC 0,6111 is.

We kunnen AUC gebruiken om de prestaties van twee of meer modellen te vergelijken. Het model met de hoogste AUC presteert het beste.

Aanvullende bronnen

Hoe logistische regressie uit te voeren in Stata
Hoe de ROC-curve en AUC van een logistisch regressiemodel te interpreteren