Hoe back-to-back stam- en bladplots te maken

Een stam- en bladdiagram is een type diagram dat gegevens weergeeft door elke waarde in een gegevensset te verdelen in een ’stam‘ en een ‚blad‘.

Stel dat we bijvoorbeeld de volgende gegevensset hebben:

Gegevensset: 12, 14, 18, 22, 22, 23, 25, 25, 28, 45, 47, 48

Als we het eerste cijfer van elke waarde definiëren als de „stengel“ en het tweede cijfer als het „blad“, kunnen we het volgende stam- en bladdiagram maken:

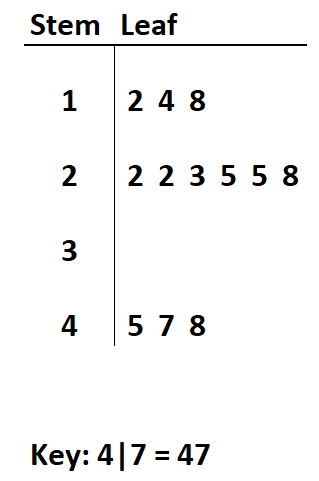
Een uitbreiding van de stengel-en-bladplot is de back-to-back stengel-en-bladplot , die kan worden gebruikt om waarden uit twee sets gegevens weer te geven.

In deze tutorial wordt uitgelegd hoe u een back-to-back stam- en bladplot maakt en hoe u deze kunt gebruiken om vragen over twee sets gegevens te beantwoorden.

Hoe u een back-to-back stam- en bladplot kunt maken

Stel dat we de volgende twee sets gegevens hebben die het aantal punten weergeven dat is gescoord door leden van twee basketbalteams:

Buitenbeentjes: 2, 4, 8, 12, 12, 12, 15, 19, 23, 25, 31, 35, 38

Lakers: 6, 6, 7, 12, 13, 15, 16, 20, 22, 24, 28, 30, 31

Om een back-to-back stam-bladplot voor deze gegevenssets te maken, kunnen we een enkele ‘stam’ maken die het eerste cijfer van elke waarde vertegenwoordigt, en een reeks ‘bladeren’ die zich aan weerszijden van de stengel vertakken en die vertegenwoordigt het tweede cijfer van elke waarde:

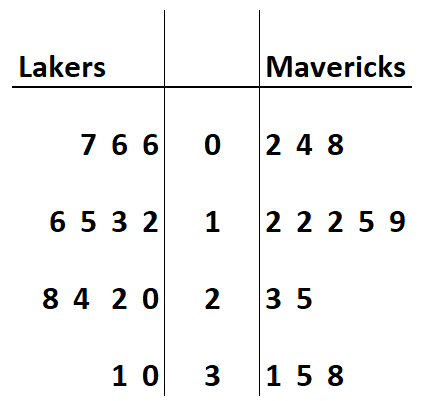
Punten gescoord door leden van de Mavericks worden weergegeven aan de rechterkant van het bovenwerk en punten gescoord door leden van de Lakers worden weergegeven aan de linkerkant van het bovenwerk.

Merk op dat er aan elke kant van de stengel 13 individuele waarden worden weergegeven, die de 13 datawaarden voor elke dataset vertegenwoordigen.

Een back-to-back stengel- en bladplot is handig omdat we hiermee eenvoudig de verdeling van waarden in twee datasets tegelijkertijd kunnen visualiseren en twee verdelingen snel kunnen vergelijken.

Hoe een back-to-back stengel- en bladplot te interpreteren

Zodra we een back-to-back stengel- en bladplot hebben, kunnen we deze gebruiken om vragen te beantwoorden over elk van de twee gegevenssets die in de plot worden weergegeven.

Vraag 1: Wat is het bereik van de punten die voor elk team worden gescoord?

Houd er rekening mee dat het bereik het verschil is tussen de grootste en de kleinste waarde.

• Bereik voor de Mavericks: 38 – 2 = 36
• Bereik voor de Lakers: 31 – 6 = 25

Vraag 2: Wat is het aantal gescoorde punten voor elk team?

Houd er rekening mee dat de modus de waarde is die het vaakst voorkomt.

• Mode voor de Mavericks: 12
• Mode voor de Lakers: 6

Vraag 3: Wat is het gemiddelde aantal gescoorde punten voor elk team?

Bedenk dat de mediaan de ‘gemiddelde’ waarde in een dataset is.

• Mediaan voor de Mavericks: 15
• Mediaan voor Lakers: 16

Vraag 4: Bij welk team scoorden de meeste spelers 20 of meer punten?

• Spelers die 20 of meer scoorden voor de Mavericks: 5
• Spelers die 20 of meer scoorden voor de Lakers: 6

De Lakers hadden meer spelers die 20 of meer punten scoorden.

Vraag 5: Welk team had de best presterende speler?

• Topscorer voor de Mavericks: 38
• Lakers-topscorer: 31

De Mavericks hadden de best presterende speler.

Aanvullende bronnen

Een inleiding tot stam- en bladplots
Stam- en bladplotgenerator
Hoe u een stam- en bladplot maakt in Excel