Hoe u de proc glmselect-instructie in sas gebruikt

U kunt de PROC GLMSELECT- instructie in SAS gebruiken om het beste regressiemodel te selecteren op basis van een lijst met potentiële voorspellende variabelen.

Het volgende voorbeeld laat zien hoe u deze verklaring in de praktijk kunt gebruiken.

Voorbeeld: hoe u PROC GLMSELECT in SAS gebruikt voor modelselectie

Stel dat we een meervoudig lineair regressiemodel willen toepassen dat (1) het aantal uren besteed aan studeren, (2) het aantal afgelegde voorbereidende examens en (3) geslacht gebruikt om het eindcijfer van het examen van studenten te voorspellen.

Eerst gebruiken we de volgende code om een dataset te maken met deze informatie voor 20 studenten:

 /*create dataset*/
data exam_data;
    input hours prep_exams gender $score;
    datalines ;
1 1 0 76
2 3 1 78
2 3 0 85
4 5 0 88
2 2 0 72
1 2 1 69
5 1 1 94
4 1 0 94
2 0 1 88
4 3 0 92
4 4 1 90
3 3 1 75
6 2 1 96
5 4 0 90
3 4 0 82
4 4 1 85
6 5 1 99
2 1 0 83
1 0 1 62
2 1 0 76
;
run ;

/*view dataset*/
proc print data =exam_data;

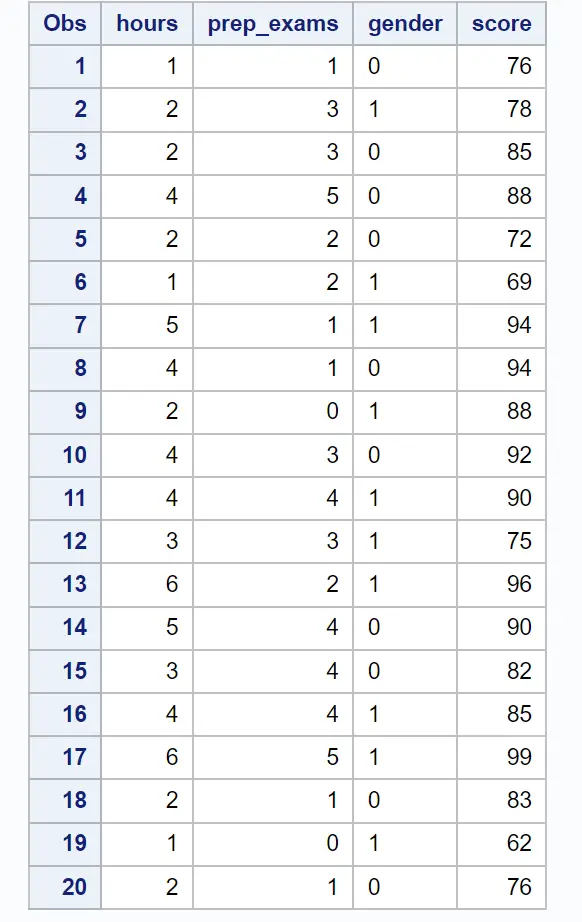
Vervolgens zullen we de PROC GLMSELECT -instructie gebruiken om de subset van voorspellende variabelen te identificeren die het beste regressiemodel oplevert:

 /*perform model selection*/
proc glmselect data =exam_data;
    classgender ;
    model score = hours prep_exams gender;
run ;

Opmerking : we hebben geslacht in de klasse- instructie opgenomen omdat het een categorische variabele is.

De eerste groep tabellen in de uitvoer toont een overzicht van de GLMSELECT-procedure:

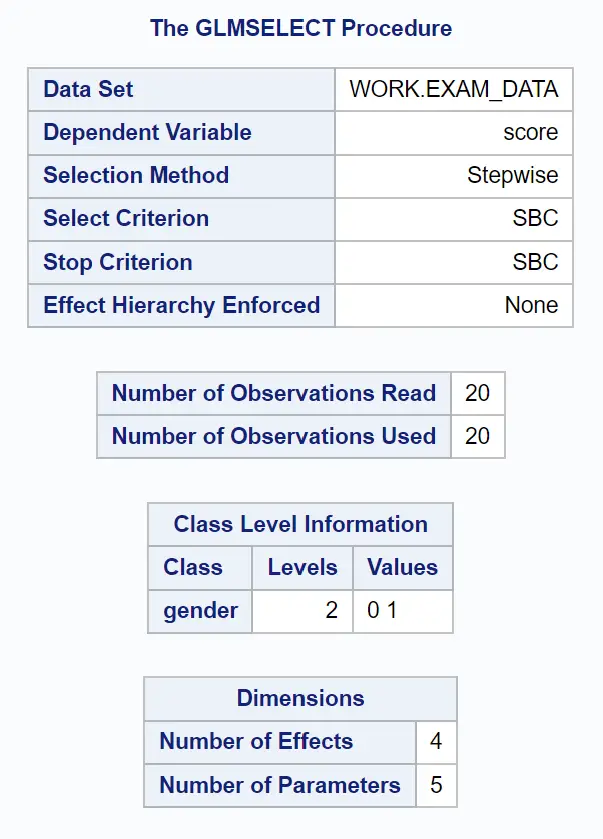
We kunnen zien dat het criterium dat werd gebruikt om te stoppen met het toevoegen of verwijderen van variabelen uit het model SBC was, wat het Schwarz-informatiecriterium is, ook wel het Bayesiaanse informatiecriterium genoemd.

In wezen gaat de PROC GLMSELECT -instructie door met het toevoegen of verwijderen van variabelen uit het model totdat het model met de laagste SBC-waarde wordt gevonden, wat als het „beste“ model wordt beschouwd.

De volgende groep tabellen laat zien hoe de stapsgewijze selectie eindigde:

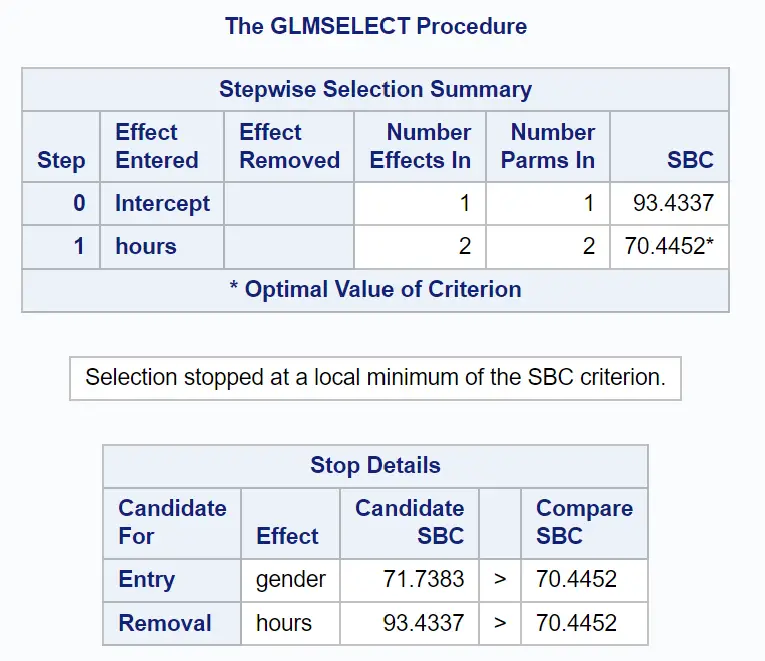
We kunnen zien dat een model met alleen de oorspronkelijke term een SBC-waarde van 93,4337 had.

Door uren toe te voegen als voorspellende variabele in het model daalde de SBC-waarde naar 70,4452 .

De beste manier om het model te verbeteren was door geslacht als voorspellende variabele toe te voegen, maar hierdoor steeg de SBC-waarde feitelijk naar 71,7383.

Het uiteindelijke model omvat dus alleen de interceptterm en de bestudeerde tijden.

Het laatste deel van het resultaat toont de samenvatting van dit gepaste regressiemodel:

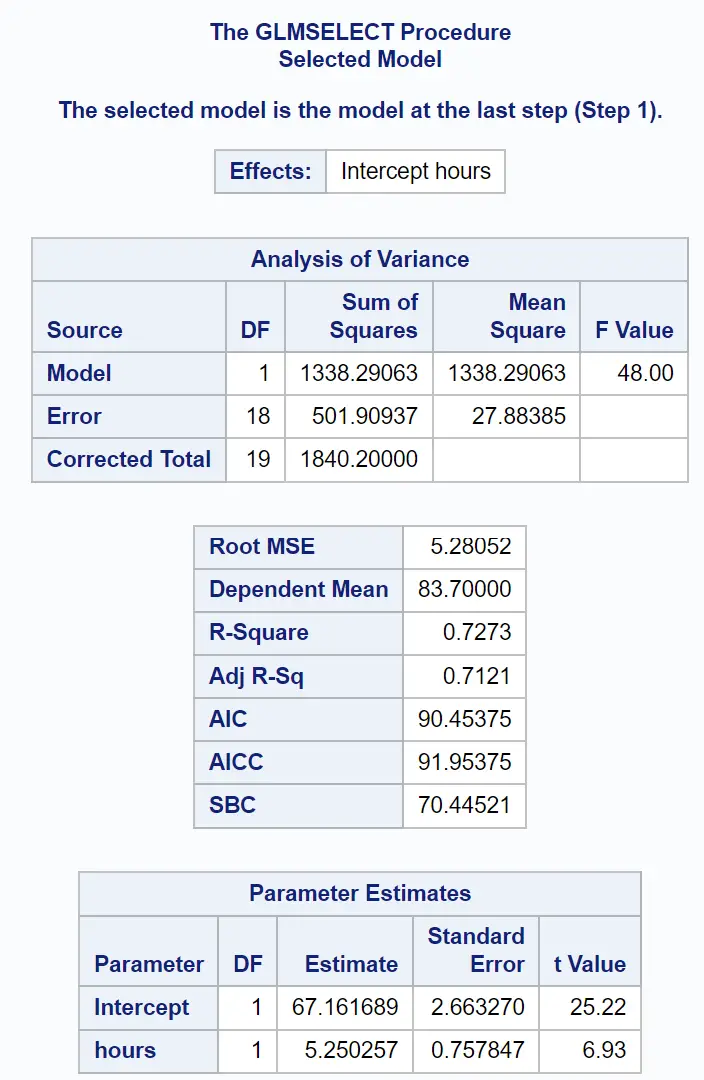
We kunnen de waarden in de tabel Parameterschattingen gebruiken om het gepaste regressiemodel te schrijven:

Examenscore = 67,161689 + 5,250257 (uren gestudeerd)

We kunnen ook verschillende statistieken zien die ons vertellen hoe goed dit model bij de gegevens past:

De R-Square- waarde vertelt ons het percentage variatie in examenscores dat kan worden verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.

In dit geval kan 72,73% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.

Ook de Root MSE- waarde is handig om te weten. Dit vertegenwoordigt de gemiddelde afstand tussen de waargenomen waarden en de regressielijn.

In dit regressiemodel wijken de waargenomen waarden gemiddeld 5,28052 eenheden af van de regressielijn.

Opmerking : Raadpleeg de SAS-documentatie voor een volledige lijst met mogelijke argumenten die u kunt gebruiken met PROC GLMSELECT .

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe polynomiale regressie uit te voeren in SAS
Hoe logistische regressie uit te voeren in SAS