Semi-interkwartielbereik
In dit artikel wordt uitgelegd wat het semi-interkwartielbereik in de statistiek is. U vindt dus hoe u het semi-interkwartielbereik kunt berekenen, een opgeloste oefening en bovendien een online rekenmachine om het semi-interkwartielbereik van elk gegevensmonster te berekenen.
Wat is de semi-interkwartielafstand?
Het semi-interkwartielbereik (of semi-interkwartielbereik ) is de helft van het verschil tussen het eerste en het derde kwartiel. Om het semi-interkwartielbereik te berekenen, moet u daarom het derde kwartiel min het eerste kwartiel aftrekken en vervolgens door twee delen.
Het semi-interkwartielbereik is een maatstaf voor de spreiding die de variabiliteit van centrale waarden aangeeft. Dus hoe groter het semi-interkwartielbereik van een dataset, hoe meer verspreid de waarden in het midden ten opzichte van elkaar zijn.
Een van de kenmerken van de semi-interkwartielafstand is dat het een robuuste statistische parameter is, zodat uitschieters geen invloed hebben op de semi-interkwartielafstand.
Het semi-interkwartielinterval is dus een spreidingsmaatstaf die vergelijkbaar is met het statistische interval, aangezien het de variabiliteit van een gegevensset aangeeft door twee kwartielwaarden af te trekken. Het statistische bereik wordt echter iets anders berekend.
Formule voor semi-interkwartielbereik
Het semi-interkwartielbereik is gelijk aan het verschil tussen het derde kwartiel en het eerste kwartiel gedeeld door twee. Om het semi-interkwartielbereik te berekenen, moet u daarom eerst het eerste en derde kwartiel vinden, deze vervolgens aftrekken en ten slotte het aftrekkingsresultaat door twee delen.
De formule voor het berekenen van het semi-interkwartielbereik is dus:
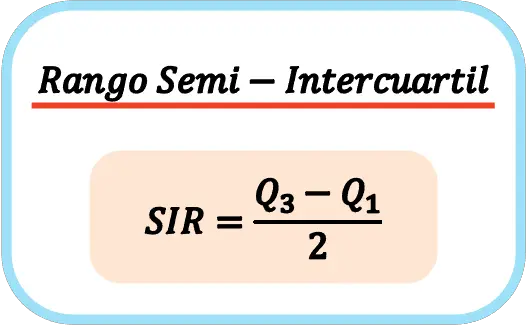
👉 U kunt de onderstaande rekenmachine gebruiken om het semi-interkwartielbereik van elke dataset te berekenen.
Om het semi-interkwartielbereik weer te geven, wordt doorgaans het acroniem SIR ( Semi Intquartile Range ) gebruikt als symbool voor deze statistische maatstaf.
Kortom, de semi-interkwartielafstand is de helft van de interkwartielafstand .
Voorbeeld van het berekenen van het semi-interkwartielbereik
Nadat we de definitie van het semi-interkwartielbereik en de bijbehorende formule hebben gezien, volgt hieronder een concreet voorbeeld om duidelijk uit te leggen hoe het semi-interkwartielbereik wordt berekend.
- Wij willen statistisch analyseren of het een goed idee is om in een bedrijf te investeren. Om dit te doen, hebben we gegevens verzameld over de aandelenkoers van dit bedrijf gedurende de afgelopen 15 maanden. In de volgende tabel ziet u de waargenomen gegevens, gerangschikt van laag naar hoog. Bereken het semi-interkwartielbereik van deze dataset.

Zoals uitgelegd in het bovenstaande gedeelte moeten we, om het semi-interkwartielbereik te vinden, eerst het eerste en derde kwartiel bepalen.
Het eerste kwartiel is de mediaan van de eerste helft van de waarden, wat overeenkomt met de waarde € 8,95/aandeel.
![]()
Aan de andere kant is het derde kwartiel de tussenwaarde van de tweede helft van de waarden, namelijk € 9,83/aandeel.
![]()
Zodra we de waarden van het eerste en derde kwartiel kennen, passen we eenvoudigweg de formule voor het semi-interkwartielinterval toe om de waarde ervan te vinden:
![]()
Semi-interkwartielafstandscalculator
Voer een statistische gegevensset in de volgende online rekenmachine in om het semi-interkwartielbereik ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.