Een shapiro-wilk-test uitvoeren in r (met voorbeelden)

De Shapiro-Wilk-test is een test van normaliteit. Het wordt gebruikt om te bepalen of een steekproef wel of niet uit eennormale verdeling komt.

Dit type test is handig om te bepalen of een bepaalde gegevensset al dan niet uit een normale verdeling komt, wat een veelgebruikte aanname is in veel statistische tests, waaronder regressie , ANOVA , t-tests en vele andere. ‚anderen.

We kunnen eenvoudig een Shapiro-Wilk-test uitvoeren op een bepaalde dataset met behulp van de volgende ingebouwde functie in R:

vormro.test(x)

Goud:

• x: een numerieke vector van gegevenswaarden.

Deze functie produceert een W- teststatistiek samen met een overeenkomstige p-waarde. Als de p-waarde kleiner is dan α = 0,05, is er voldoende bewijs om te zeggen dat de steekproef niet uit een normaal verdeelde populatie komt.

Opmerking: de steekproefomvang moet tussen 3 en 5.000 liggen om de functie shapiro.test() te kunnen gebruiken.

Deze tutorial toont verschillende voorbeelden van praktisch gebruik van deze functie.

Voorbeeld 1: Shapiro-Wilk-test op normale gegevens

De volgende code laat zien hoe u een Shapiro-Wilk-test uitvoert op een gegevensset met steekproefomvang n=100:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

De p-waarde van de test blijkt 0,6303 te zijn. Omdat deze waarde niet kleiner is dan 0,05, kunnen we aannemen dat de steekproefgegevens afkomstig zijn uit een normaal verdeelde populatie.

Dit resultaat zou niet verrassend moeten zijn, aangezien we de voorbeeldgegevens hebben gegenereerd met behulp van de functie rnorm(), die willekeurige waarden genereert uit een normale verdeling met gemiddelde = 0 en standaarddeviatie = 1.

Gerelateerd: Een gids voor dnorm, pnorm, qnorm en rnorm in R

We kunnen ook een histogram maken om visueel te verifiëren dat de voorbeeldgegevens normaal verdeeld zijn:

 hist(data, col=' steelblue ') 

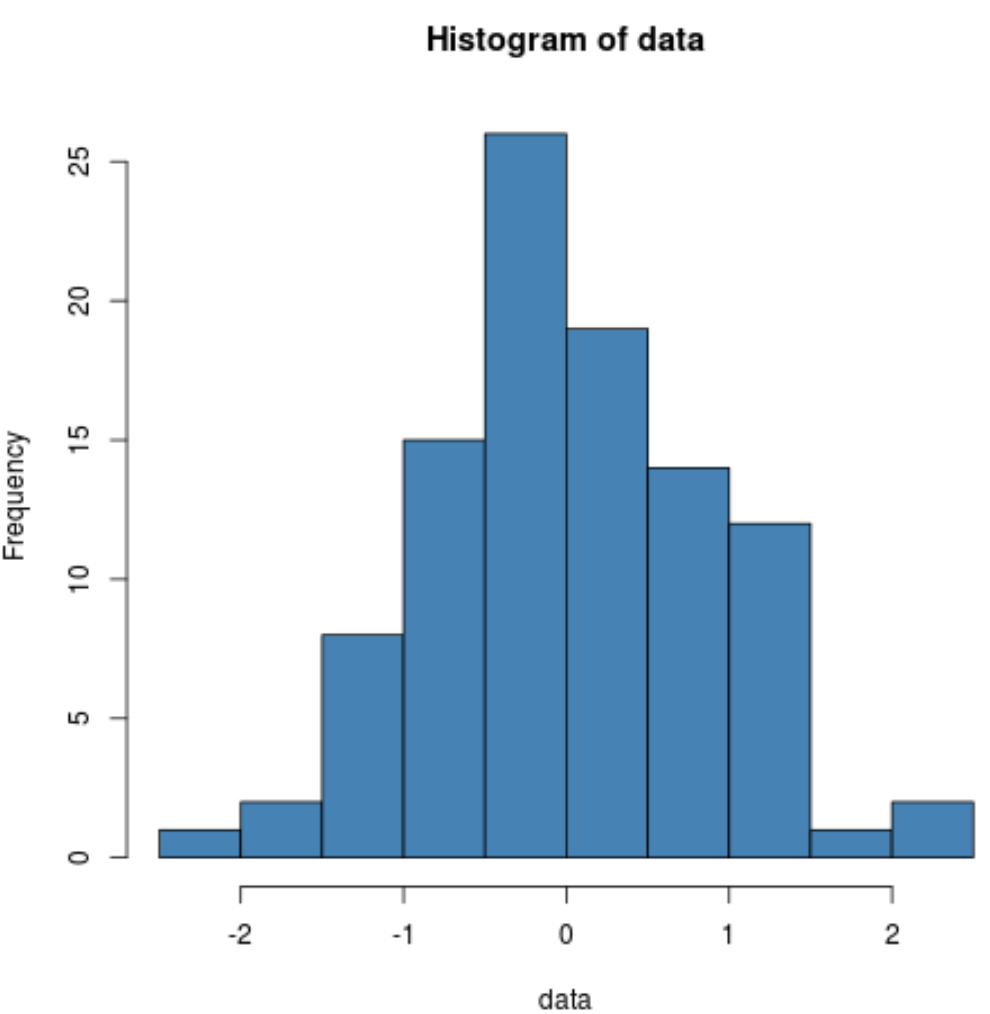
We kunnen zien dat de verdeling vrij klokvormig is met een piek in het midden van de verdeling, wat typerend is voor normaal verdeelde gegevens.

Voorbeeld 2: Shapiro-Wilk-test op niet-normale gegevens

De volgende code laat zien hoe je een Shapiro-Wilk-test uitvoert op een dataset met steekproefomvang n=100, waarbij de waarden willekeurig worden gegenereerd op basis van een Poisson-verdeling :

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

De p-waarde van de test blijkt 0,0003393 te zijn. Omdat deze waarde kleiner is dan 0,05, hebben we voldoende bewijs om te zeggen dat de steekproefgegevens niet afkomstig zijn van een normaal verdeelde populatie.

Dit resultaat zou niet verrassend moeten zijn, aangezien we de voorbeeldgegevens hebben gegenereerd met behulp van de functie rpois(), die willekeurige waarden genereert uit een Poisson-verdeling.

Gerelateerd: Een gids voor dpois, ppois, qpois en rpois in R

We kunnen ook een histogram maken om visueel te zien dat de voorbeeldgegevens niet normaal verdeeld zijn:

 hist(data, col=' coral2 ') 

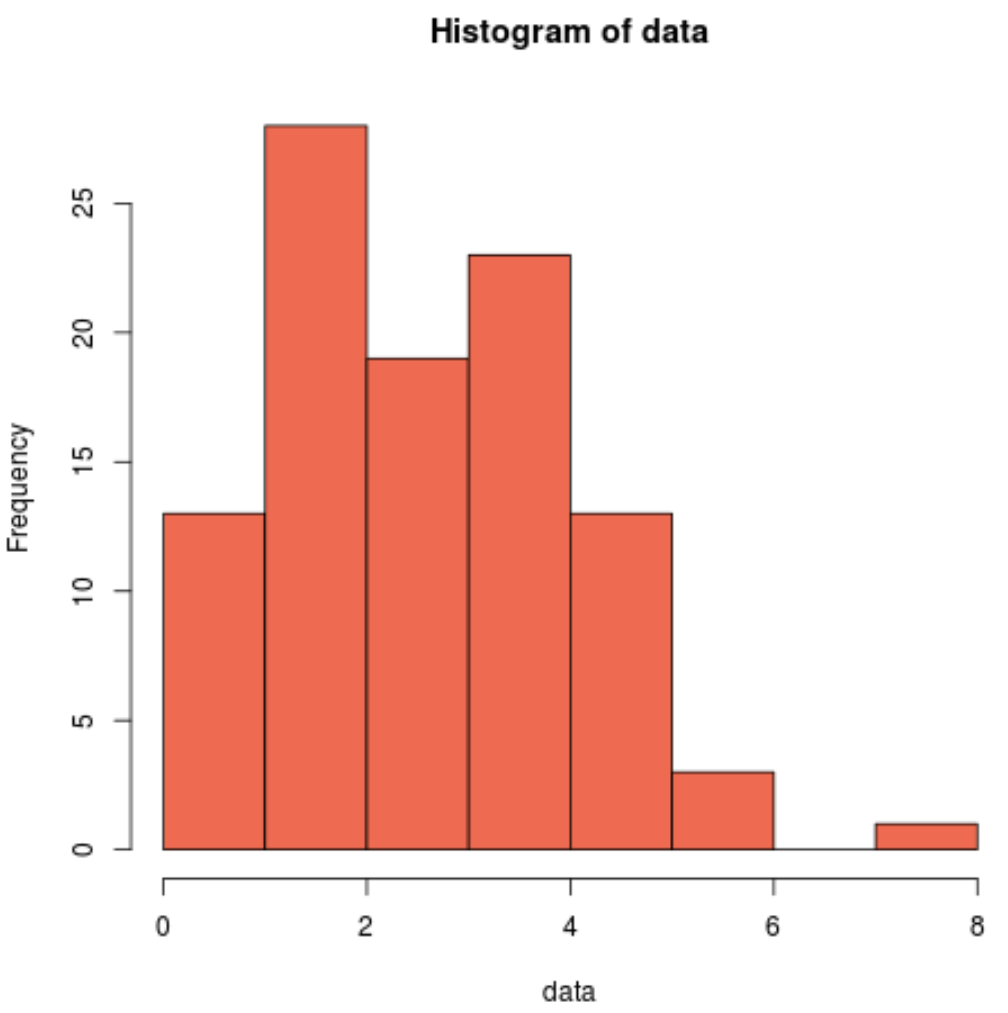
We kunnen zien dat de verdeling rechtsscheef is en niet de typische „klokvorm“ heeft die hoort bij een normale verdeling. Ons histogram komt dus overeen met de resultaten van de Shapiro-Wilk-test en bevestigt dat onze voorbeeldgegevens niet uit een normale verdeling komen.

Wat te doen met niet-normale gegevens

Als een bepaalde dataset niet normaal verdeeld is , kunnen we vaak een van de volgende transformaties uitvoeren om deze normaler te maken:

1. Logtransformatie: transformeer de responsvariabele van y naar log(y) .

2. Vierkantsworteltransformatie: Transformeer de responsvariabele van y naar √y .

3. Derdemachtsworteltransformatie: transformeer de responsvariabele van y naar y ^1/3 .

Door deze transformaties uit te voeren, benadert de responsvariabele doorgaans de normale verdeling.

Bekijk deze tutorial om te zien hoe u deze transformaties in de praktijk kunt uitvoeren.

Aanvullende bronnen

Hoe een Anderson-Darling-test uit te voeren in R
Hoe een Kolmogorov-Smirnov-test uit te voeren in R
Hoe u een Shapiro-Wilk-test uitvoert in Python