Hoe interpreteer je sig. waarden (tweezijdig) in spss

Wanneer u statistische tests uitvoert in SPSS, bevat de uitvoertabel vaak een Sig. waarde (bilateraal) .

Deze waarde vertegenwoordigt de tweezijdige p-waarde van de test.

Als deze waarde onder uw significantieniveau ligt (veel voorkomende keuzes zijn 0,05 of 0,01), dan kunt u de nulhypothese van uw test verwerpen .

Deze tutorial biedt voorbeelden van hoe u Sig interpreteert. (tweezijdige) waarde van verschillende statistische toetsen.

Voorbeeld 1: T-test met één monster

Een one-sample t-test wordt gebruikt om te testen of het gemiddelde van een populatie gelijk is aan een bepaalde waarde.

Stel bijvoorbeeld dat een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. Ze neemt een willekeurig monster van twaalf planten en registreert hun hoogte in centimeters.

Vervolgens gebruikt het deze steekproef om een t-test met één steekproef uit te voeren met de volgende nul- en alternatieve hypothesen:

• H ₀ : μ = 15 (het werkelijke populatiegemiddelde is gelijk aan 15 inch)
• H _A : μ ≠ 15 (het werkelijke populatiegemiddelde is niet gelijk aan 15 inch)

Ze voert deze one-sample t-test uit in SPSS en krijgt de volgende resultaten:

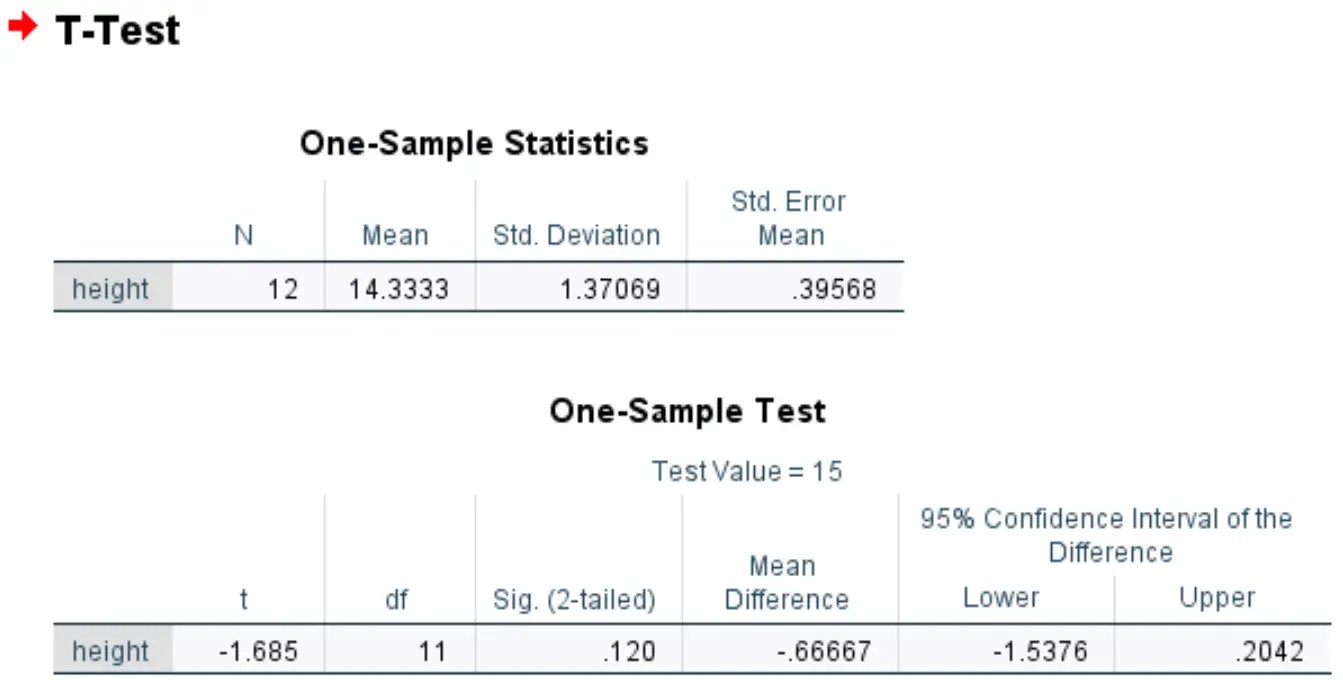
De Sig. De waarde (tweezijdig) is 0,120 .

Dit vertegenwoordigt de tweezijdige p-waarde die overeenkomt met een waarde van -1,685 met 11 vrijheidsgraden.

Omdat de p-waarde van de test (0,120) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Met andere woorden, we hebben niet genoeg bewijs om te zeggen dat de werkelijke gemiddelde hoogte van deze plantensoort iets anders is dan 45 centimeter.

Voorbeeld 2: T-test met twee steekproeven

Een two-sample t-test wordt gebruikt om te testen of de gemiddelde waarden van twee populaties gelijk zijn of niet.

Stel dat onderzoekers bijvoorbeeld willen weten of een nieuwe brandstofbehandeling een verandering in het gemiddelde aantal kilometers per gallon van een bepaalde auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij 12 auto’s de nieuwe brandstofbehandeling krijgen en 12 auto’s niet.

Onderzoekers voeren een t-test met twee steekproeven uit met de volgende nul- en alternatieve hypothesen:

• H ₀ : μ ₁ = μ ₂ (de gemiddelde mpg tussen de twee populaties is gelijk)
• H ₁ : μ ₁ ≠ μ ₂ (de gemiddelde mpg tussen de twee populaties is niet gelijk)

Ze voeren een t-test met twee steekproeven uit in SPSS en verkrijgen de volgende resultaten:

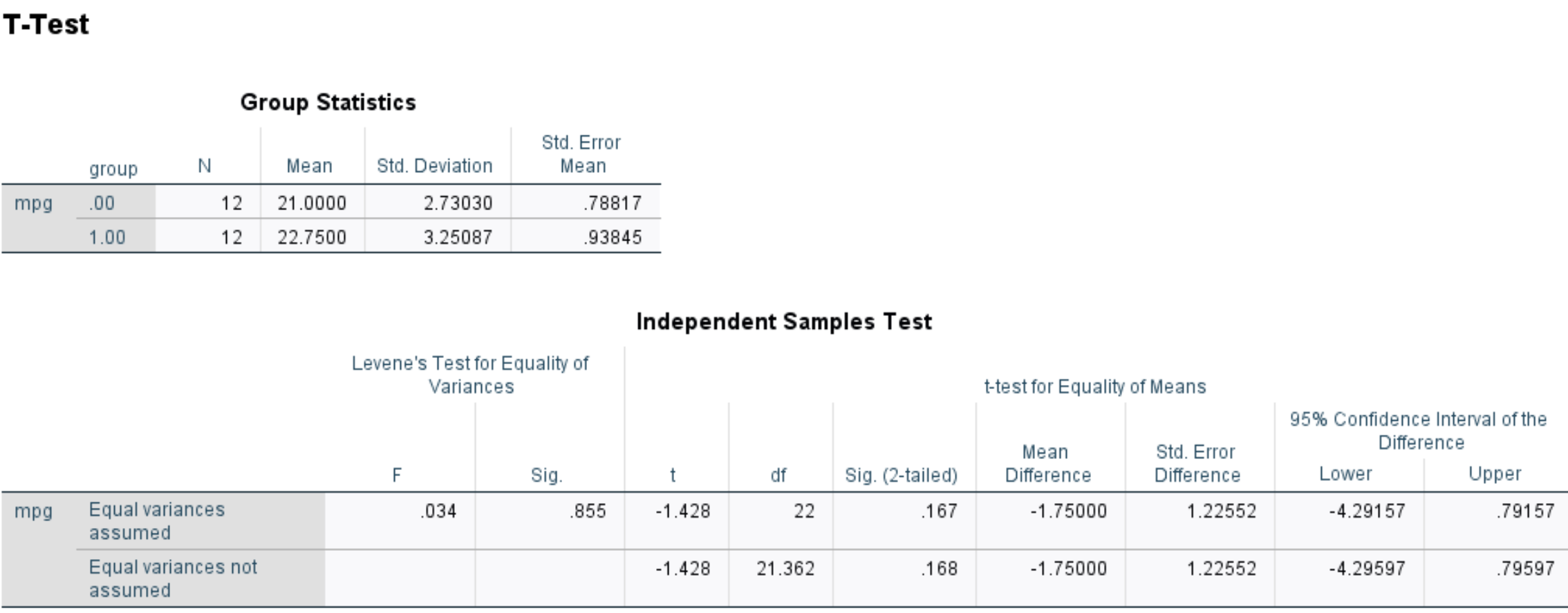
De Sig. De waarde (2-zijdig) is 0,167 .

Dit vertegenwoordigt de tweezijdige p-waarde die overeenkomt met een waarde van -1,428 met 22 vrijheidsgraden.

Omdat de p-waarde van de test (0,167) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Met andere woorden: we hebben niet genoeg bewijs om te zeggen dat het werkelijke gemiddelde mpg verschilt tussen auto’s die een behandeling ondergaan en auto’s die dat niet doen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u verschillende statistische tests uitvoert in SPSS:

Hoe u een one-sample t-test uitvoert in SPSS
Hoe u een t-test met twee steekproeven uitvoert in SPSS
Hoe u een paired samples t-test uitvoert in SPSS