Soorten asymmetrie

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel leer je hoeveel soorten asymmetrie er in de statistiek bestaan. Zo wordt elk type asymmetrie uitgelegd met voorbeelden en bovendien kun je zien hoe de asymmetrie van een verdeling wordt berekend.

Wat zijn de soorten asymmetrie?

In de statistiek zijn er drie soorten asymmetrie :

Positieve scheefheid : De verdeling heeft meer verschillende waarden rechts van het gemiddelde dan links.
Negatieve scheefheid : de verdeling heeft meer verschillende waarden links van het gemiddelde dan rechts ervan.
Symmetrie : De verdeling heeft links en rechts van het gemiddelde hetzelfde aantal waarden.

Elk type asymmetrie wordt hieronder in meer detail uitgelegd.

positieve asymmetrie

Wanneer een verdeling een positieve scheefheid heeft, betekent dit dat de rechterstaart langer is dan de linkerstaart. Dat wil zeggen dat de verdeling rechts van het gemiddelde meer verschillende waarden heeft.

De curve in het vorige voorbeeld is positief asymmetrisch omdat er veel meer waarden rechts van het gemiddelde staan dan links. Zoals u in de grafiek kunt zien, is de groene balk veel groter dan de oranje balk.

negatieve asymmetrie

In de statistieken wordt gezegd dat een verdeling een negatieve scheefheid heeft als de grafiek de linkerstaart langer heeft dan de rechterstaart. Dat wil zeggen, een negatief scheve verdeling betekent dat deze meer verschillende waarden links van het gemiddelde heeft.

Als je naar de vorige grafiek kijkt, staan er meer waarden links van het gemiddelde dan rechts, waardoor de curve negatief scheef is.

Symmetrie

Een verdeling is symmetrisch als het aantal waarden links van het gemiddelde gelijk is aan het aantal waarden rechts van het gemiddelde. Het gemiddelde fungeert daarom als een symmetrieas.

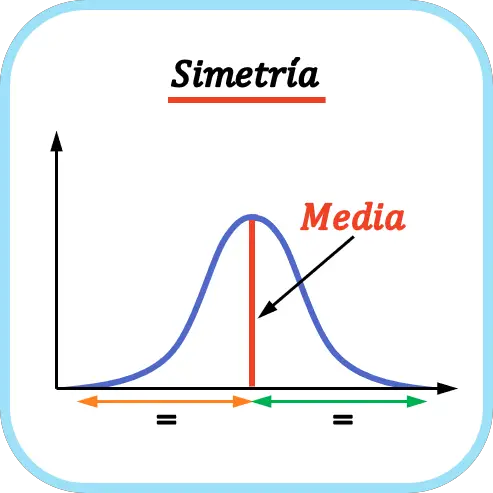
Zoals uit het bovenstaande voorbeeld blijkt, valt het aantal waarden links van het gemiddelde van de weergegeven kansverdeling samen met het aantal waarden rechts van het gemiddelde, dus er is sprake van een symmetrische verdeling.

Hoe het type asymmetrie te bepalen

Nu we weten wat de verschillende typen asymmetrie in de statistiek zijn, gaan we kijken hoe we kunnen weten met welk type asymmetrie een kansverdeling overeenkomt.

Traditioneel wordt uitgelegd dat we het type scheefheid van een verdeling kunnen kennen op basis van de relatie tussen het gemiddelde en de mediaan (of deze nu groter, gelijkwaardig of kleiner is). Deze eigenschap is echter niet altijd tevreden. Om de scheefheid van een verdeling te bepalen, moet dus de scheefheidscoëfficiënt van Fisher worden berekend.

De Fisher-asymmetriecoëfficiënt wordt berekend met behulp van de volgende formule:

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

Of gelijkwaardig:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

Goud

$E$

is de wiskundige verwachting ,

$\mu$

het rekenkundig gemiddelde en

$\sigma$

de standaarddeviatie .

En zodra de Fisher-coëfficiënt is berekend, maakt het teken het mogelijk om te bepalen welk type asymmetrie de verdeling vertoont:

Als de scheefheidscoëfficiënt van Fisher positief is, is de verdeling positief scheef.
Als de scheefheidscoëfficiënt van Fisher negatief is, is de verdeling negatief scheef.
Als de verdeling symmetrisch is, is de scheefheidscoëfficiënt van Fisher gelijk aan nul (het omgekeerde is niet altijd waar).

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder