Gemiddelde typen (statistieken)

Von Dr.benjamin anderson August 6, 2023 Statistieken Keine Kommentare

Hier leggen we uit wat alle soorten gemiddelden in statistieken zijn en hoe ze worden berekend. Per koussoort vindt u de formule en voorbeelden.

Maar voordat we zien wat de soorten gemiddelden zijn, moeten we logischerwijs weten wat een gemiddelde in de statistieken is. Daarom raden wij u aan de volgende link te raadplegen voordat u verdergaat.

➤ Zie: Wat is het gemiddelde (statistieken)?

Wat zijn de soorten gemiddelden in statistieken?

In de statistieken zijn de soorten gemiddelden:

Rekenkundig gemiddelde
Gewogen gemiddelde
Geometrische middelen
wortel betekent vierkant
harmonische betekenis
gegeneraliseerd gemiddelde
gegeneraliseerd f-gemiddelde
getrimde middelen
interkwartiel gemiddelde
gemiddelde van een functie

Vervolgens leggen we uit hoe je alle soorten gemiddelden in statistieken kunt berekenen. De vijf meest gebruikte typen gemiddelden zijn het rekenkundig gemiddelde, het gewogen gemiddelde, het geometrische gemiddelde, het kwadratische gemiddelde en het harmonische gemiddelde. We gaan dus dieper in op deze vijf hoofdtypen media.

Rekenkundig gemiddelde

Het rekenkundig gemiddelde wordt berekend door alle waarden bij elkaar op te tellen en vervolgens te delen door het totale aantal datapunten.

De formule voor het rekenkundig gemiddelde is daarom als volgt:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

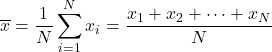
Het rekenkundig gemiddelde wordt ook wel het rekenkundig gemiddelde genoemd.

Het rekenkundig gemiddelde is waarschijnlijk het meest gebruikte type gemiddelde in de statistiek.

Om een voorbeeld te zien van hoe dit type gemiddelde wordt verkregen, berekenen we het rekenkundig gemiddelde van de volgende gegevens:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Om het rekenkundig gemiddelde te berekenen, hoeft u alleen maar alle statistische gegevens bij elkaar op te tellen en te delen door het totale aantal gegevens, dat is 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Gewogen gemiddelde

Om het gewogen gemiddelde te berekenen, moet u eerst alle statistische gegevens vermenigvuldigen met het gewicht (of gewicht), vervolgens alle producten bij elkaar optellen en ten slotte de gewogen som delen door de som van alle gewichten.

De gewogen gemiddelde formule is daarom als volgt:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

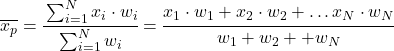
Waar x _i de statistische waarde is en w _i het bijbehorende gewicht.

Het gewogen gemiddelde is moeilijker te begrijpen, daarom raden we u aan het volgende voorbeeld te bekijken, waarin stap voor stap wordt uitgelegd hoe het wordt berekend:

➤ Zie: Voorbeeld van gewogen gemiddelde

Geometrische middelen

Het geometrische gemiddelde van een reeks statistische gegevens is gelijk aan de n-de wortel van het product van alle waarden.

Dit type gemiddelde wordt in de bedrijfsfinanciering gebruikt om rendementen, procentuele gemiddelden en samengestelde rente te berekenen.

De formule voor dit type opslag is behoorlijk ingewikkeld. In feite kan het geometrische gemiddelde van alle statistische verzamelingen niet worden berekend, maar soms kan dit type gemiddelde niet worden bepaald. Daarom raden wij u aan alle uitzonderingen te raadplegen die worden uitgelegd in de volgende link:

➤ Zie: formule voor geometrische gemiddelden

wortel betekent vierkant

Het wortelgemiddelde kwadraat is gelijk aan de vierkantswortel van het rekenkundig gemiddelde van de kwadraten van de gegevens.

De gemiddelde kwadratenformule is daarom als volgt:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Dit type gemiddelde wordt ook wel root mean square , root mean square of RMS genoemd.

Laten we er even op wijzen dat het kubieke gemiddelde ook bestaat, maar dat dit in zeer speciale gevallen wordt gebruikt.

Kwadratisch middelen heeft voor- en nadelen. Het is bijvoorbeeld vooral handig wanneer de statistische variabele positieve en negatieve waarden aanneemt, omdat door elk stukje gegevens te kwadrateren alle waarden positief worden. U kunt meer functies van dit mediatype bekijken door op de volgende link te klikken:

➤ Zie: voor- en nadelen van root mean square

harmonische betekenis

Het harmonische gemiddelde wordt berekend door het totale aantal statistische gegevens te delen door de som van de reciprocals van elke waarde.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

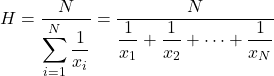
Het harmonische gemiddelde wordt gebruikt om gemiddelde snelheden, tijden te berekenen of elektronische berekeningen te maken. Dit kenmerk onderscheidt het harmonische gemiddelde van andere soorten gemiddelden, die vaak worden gebruikt bij de berekening van prijsgemiddelden of percentages.

Op de volgende pagina vindt u voorbeelden van de berekening van dit type gemiddelde:

➤ Zie: voorbeelden van harmonische betekenis

Andere soorten kousen

In deze sectie zullen we de formules voor andere soorten kousen zien. We zullen niet in detail treden over elk type omdat ze niet veel worden gebruikt, maar het is goed voor je om te weten dat er andere soorten kousen zijn.

Het gegeneraliseerde gemiddelde is een combinatie van de hierboven genoemde gemiddelde typen en wordt berekend met behulp van de volgende formule:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

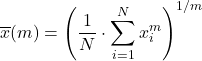
Laat f een injectieve en monotone functie zijn, dan wordt het gegeneraliseerde f-gemiddelde gedefinieerd als:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

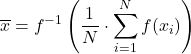
Het getrimde gemiddelde omvat het berekenen van het rekenkundig gemiddelde na het aftrekken van een percentage van de waarnemingen aan de boven- en onderkant van het monster. Aan beide kanten moet hetzelfde percentage worden afgewezen.

Om het interkwartielgemiddelde , ook wel het interkwartielgemiddelde genoemd, te berekenen, worden eerst de gegevens uit het eerste en het vierde kwartiel weggegooid, en vervolgens wordt alleen het rekenkundig gemiddelde van het tweede en derde kwartiel van de steekproef berekend. De formule voor dit type gemiddelde is daarom:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

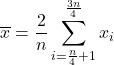
Tenslotte kun je ook het gemiddelde van een functie vinden. De gemiddelde waarde van een continue functie op een gesloten interval [a,b] wordt berekend met behulp van de volgende formule:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Steekproef- en populatiegemiddelde

Ten slotte zullen we zien wat het verschil is tussen het steekproefgemiddelde en het populatiegemiddelde, twee soorten gemiddelden die vaak met elkaar worden verward.

Het steekproefgemiddelde is het gemiddelde berekend over de waarden van een statistische steekproef, dat wil zeggen dat het wordt berekend over een deel van alle waarden van een variabele.

Het populatiegemiddelde is het gemiddelde berekend over een statistische populatie, dat wil zeggen over alle waarden van een variabele. Daarom valt het populatiegemiddelde samen met de wiskundige verwachting van de variabele.

Het steekproefgemiddelde kan als vrijwel gelijk aan het populatiegemiddelde worden beschouwd als er een voldoende grote hoeveelheid gegevens bekend is. Maar de waarde van het populatiegemiddelde is erg moeilijk te verkrijgen, omdat in werkelijkheid zelden alle waarden van een verdeling bekend zijn.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder