Hoe spearman rank-correlatie in excel te berekenen
In de statistiek verwijst correlatie naar de sterkte en richting van een verband tussen twee variabelen. De waarde van een correlatiecoëfficiënt kan variëren van -1 tot 1, met de volgende interpretaties:
- -1: een perfect negatief verband tussen twee variabelen
- 0: geen verband tussen twee variabelen
- 1: een perfecte positieve relatie tussen twee variabelen
Een speciaal type correlatie wordt de rangcorrelatie van Spearman genoemd, die wordt gebruikt om de correlatie tussen twee gerangschikte variabelen te meten. (bijvoorbeeld de rangorde van de wiskunde-examenscore van een leerling in verhouding tot de rangorde van de wetenschapsexamenscore in een klas).
In deze zelfstudie wordt uitgelegd hoe u de Spearman-rangcorrelatie tussen twee variabelen in Excel kunt berekenen.
Voorbeeld: Spearman-rangcorrelatie in Excel
Voer de volgende stappen uit om de Spearman-rangcorrelatie te berekenen tussen de wiskunde-examenscore en de wetenschapsexamenscore van 10 leerlingen in een bepaalde klas.
Stap 1: Voer de gegevens in.
Voer de examenresultaten van elke student in twee afzonderlijke kolommen in:
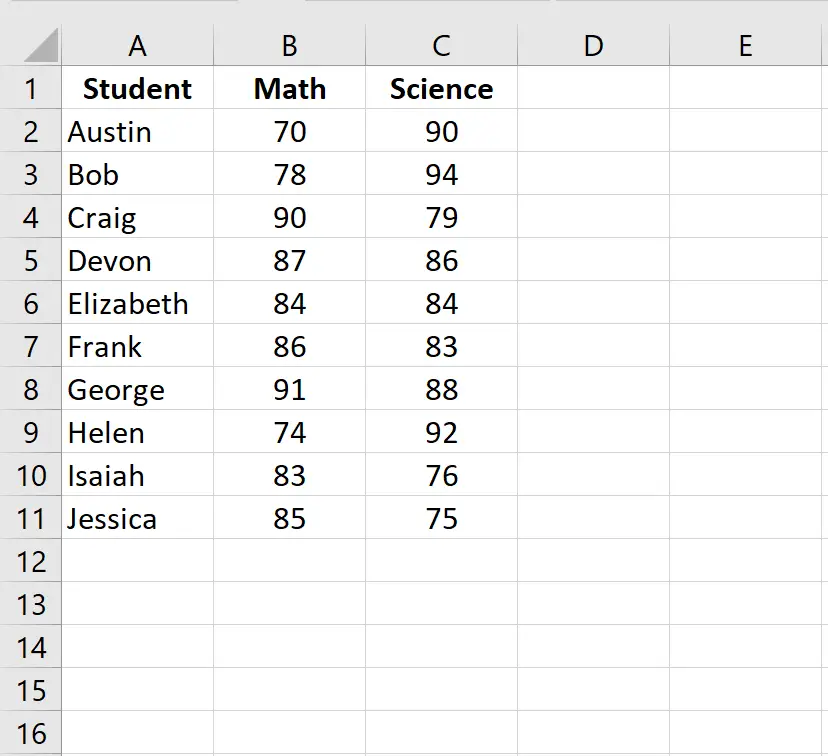
Stap 2: Bereken de ranglijst voor elke examenscore.
Vervolgens berekenen we de rangschikking voor elke examenscore. Gebruik de volgende formules in de cellen D2 en E2 om de wiskunde- en natuurwetenschappenrangen voor de eerste leerling, Austin, te berekenen:
Cel D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Cel E2: =RANK.AVG(C2, $C$2:$C$11, 0)
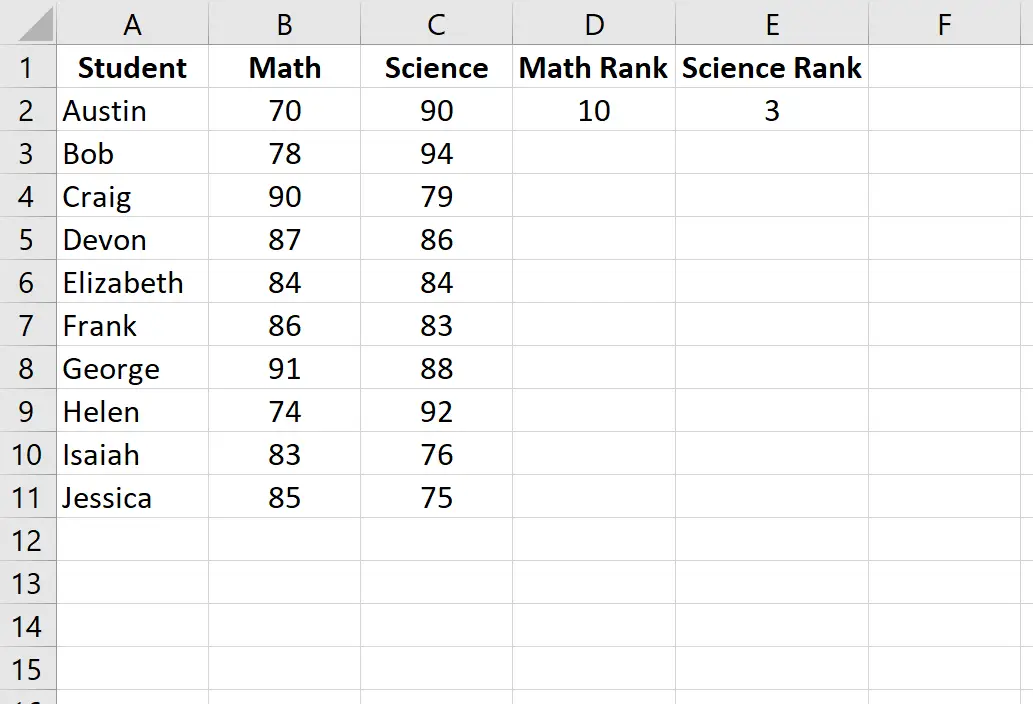
Markeer vervolgens de resterende cellen die u wilt vullen:
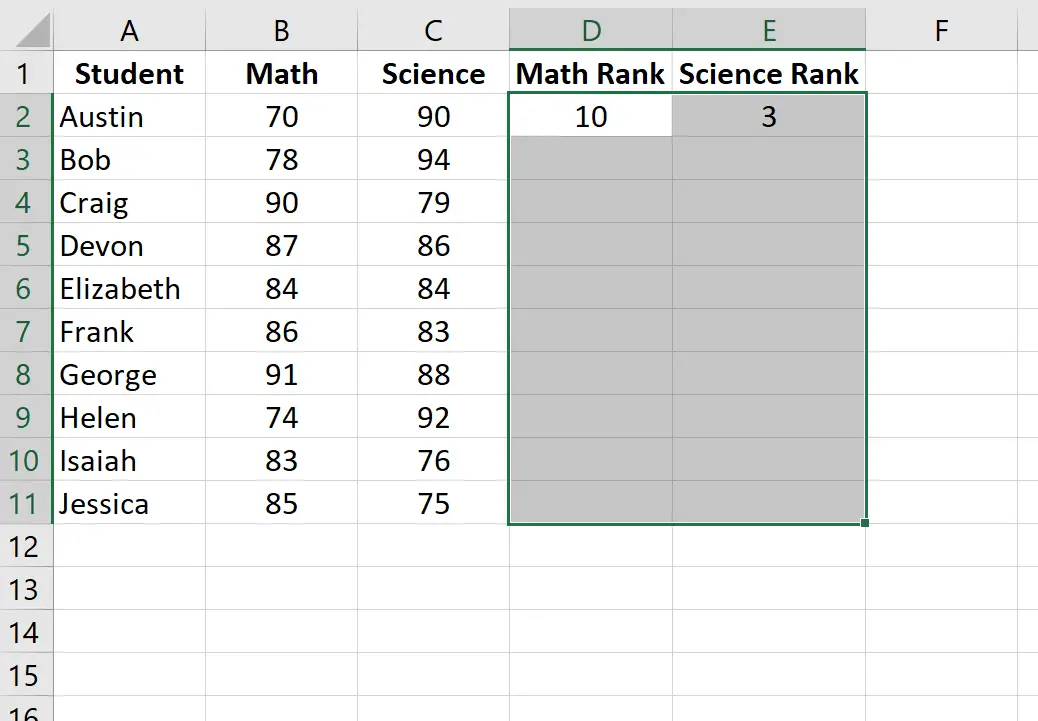
Klik vervolgens op Ctrl+D om de ranglijst van elke student in te voeren:
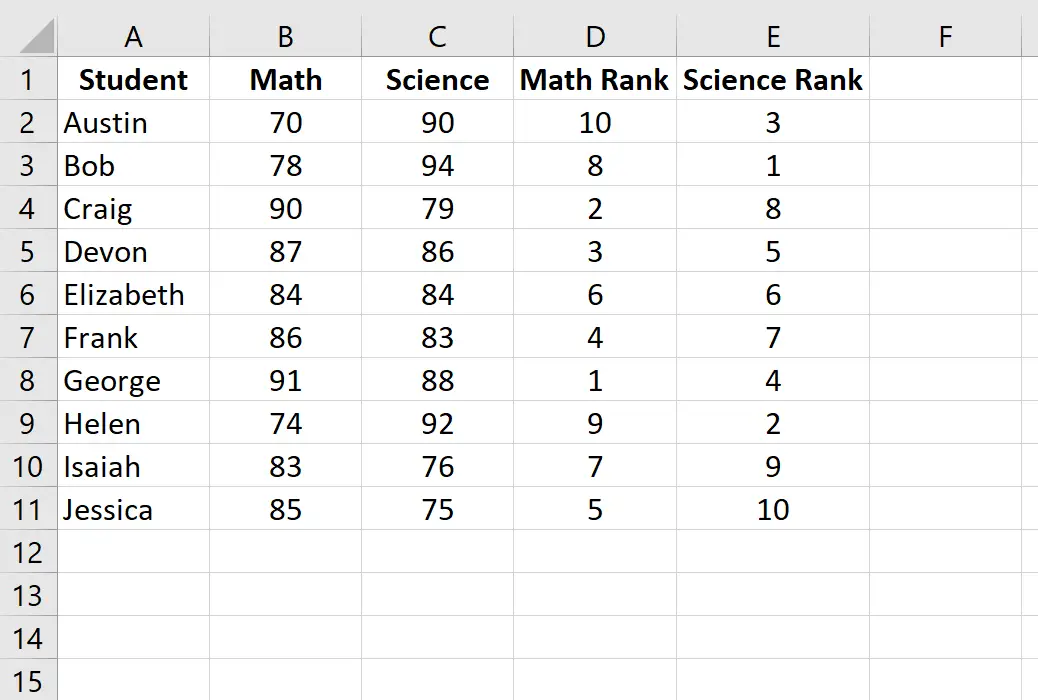
Stap 3: Bereken de Spearman-rangcorrelatiecoëfficiënt.
Ten slotte zullen we de Spearman-rangcorrelatiecoëfficiënt berekenen tussen de wiskundescores en de wetenschapsscores met behulp van de CORREL()- functie:
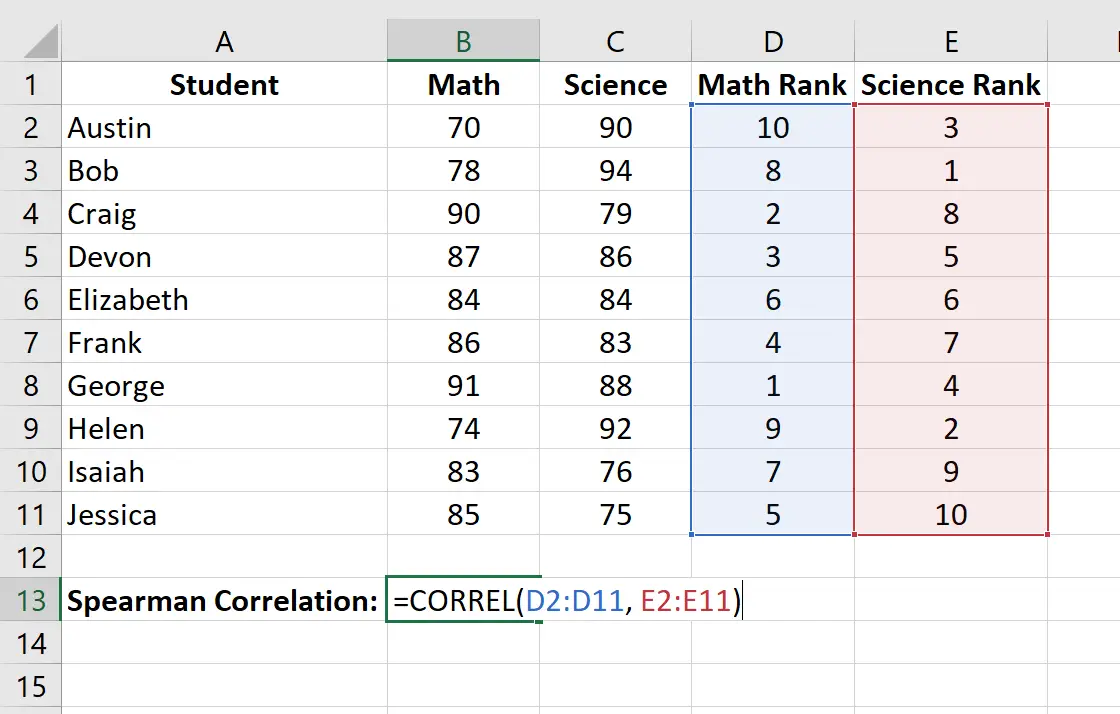
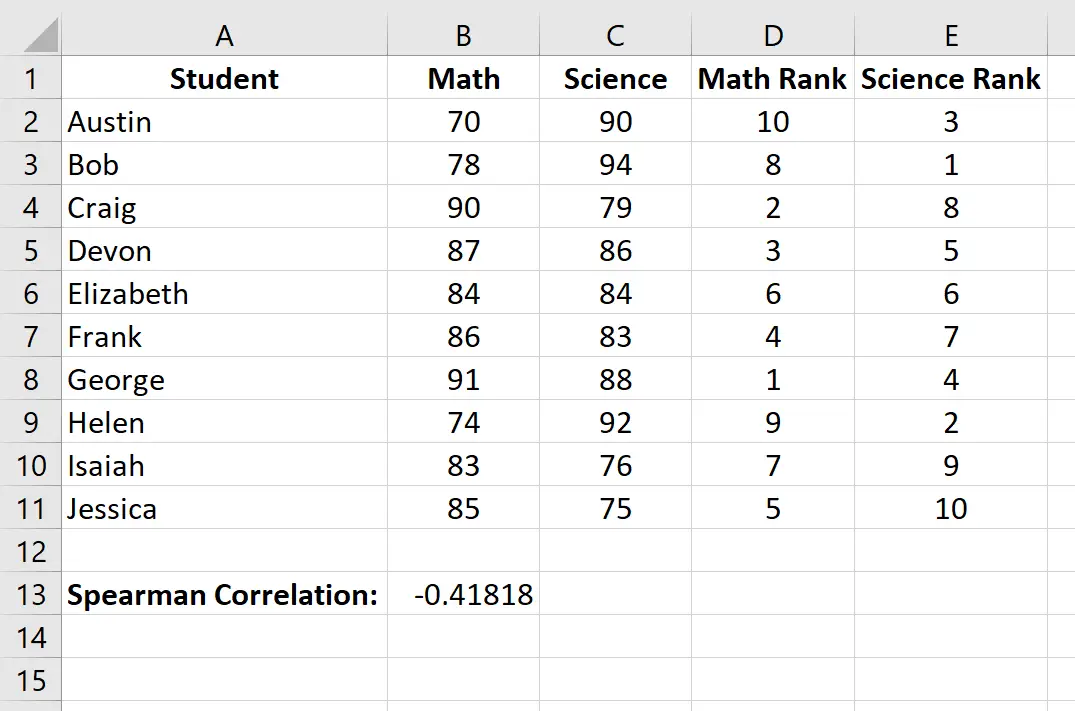
De Spearman-rangcorrelatie blijkt -0,41818 te zijn.
Stap 4 (Optioneel): Bepaal of de Spearman-rangcorrelatie statistisch significant is.
In de vorige stap hebben we vastgesteld dat de Spearman-rangcorrelatie tussen wiskunde- en natuurkundeexamenscores -0,41818 was, wat wijst op een negatieve correlatie tussen de twee variabelen.
Om echter te bepalen of deze correlatie statistisch significant is, moeten we verwijzen naar een Spearman-rangcorrelatietabel met kritische waarden, die de kritische waarden toont die verband houden met verschillende steekproefgroottes (n) en significantieniveaus (α).
Als de absolute waarde van onze correlatiecoëfficiënt groter is dan de kritische waarde in de tabel, dan is de correlatie tussen de twee variabelen statistisch significant.
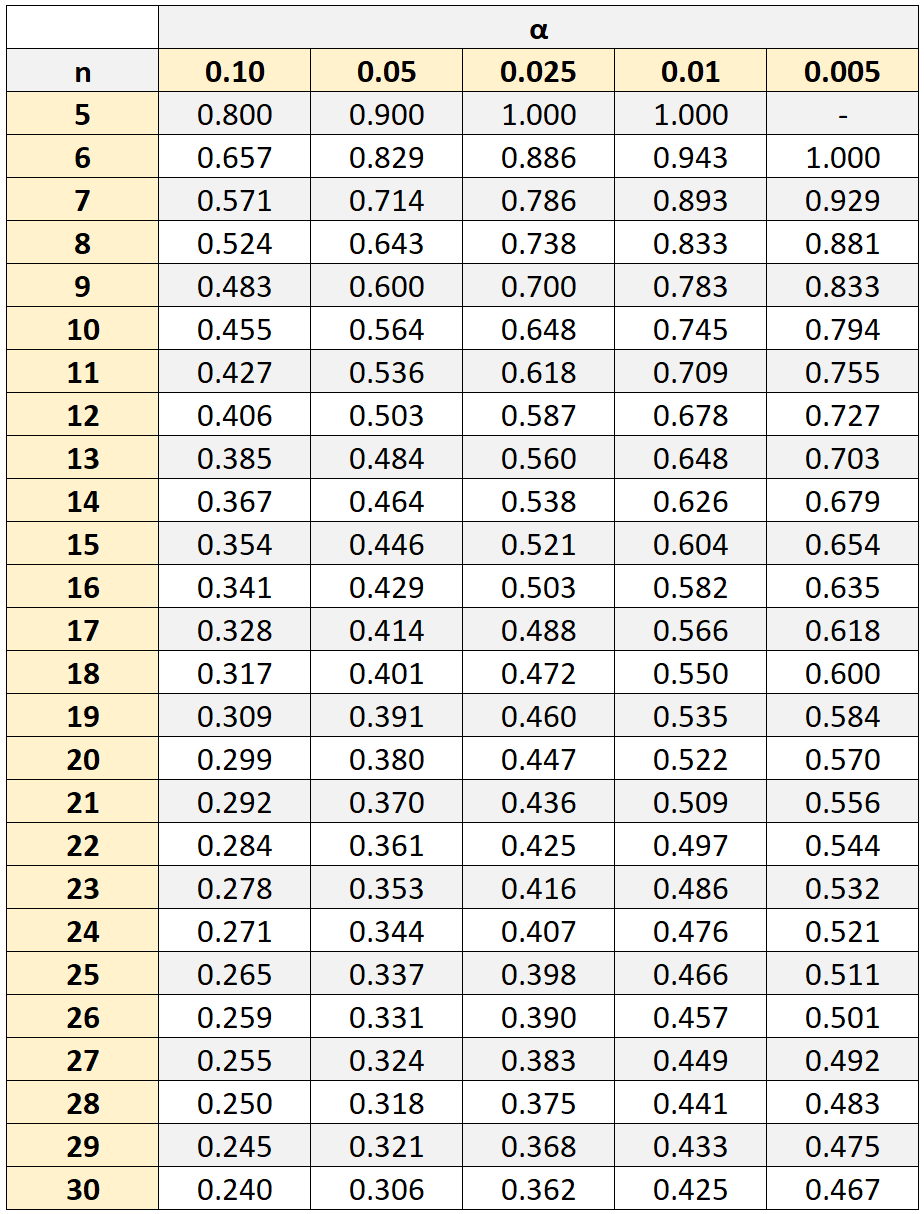
In ons voorbeeld was onze steekproefomvang n = 10 studenten. Als we een significantieniveau van 0,05 gebruiken, vinden we dat de kritische waarde 0,564 is.
Omdat de absolute waarde van de door ons berekende Spearman-rangcorrelatiecoëfficiënt ( 0,41818 ) niet groter is dan deze kritische waarde, betekent dit dat de correlatie tussen wiskunde- en natuurwetenschappenscores niet statistisch significant is.