Spline-regressie uitvoeren in r (met voorbeeld)

Spline-regressie is een type regressie dat wordt gebruikt wanneer er punten of „knopen“ zijn waar het patroon in de gegevens abrupt verandert en lineaire regressie en polynomiale regressie niet flexibel genoeg zijn om in de gegevens te passen.

Het volgende stapsgewijze voorbeeld laat zien hoe u spline-regressie uitvoert in R.

Stap 1: Creëer de gegevens

Laten we eerst een gegevensset in R maken met twee variabelen en een spreidingsdiagram maken om de relatie tussen de variabelen te visualiseren:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

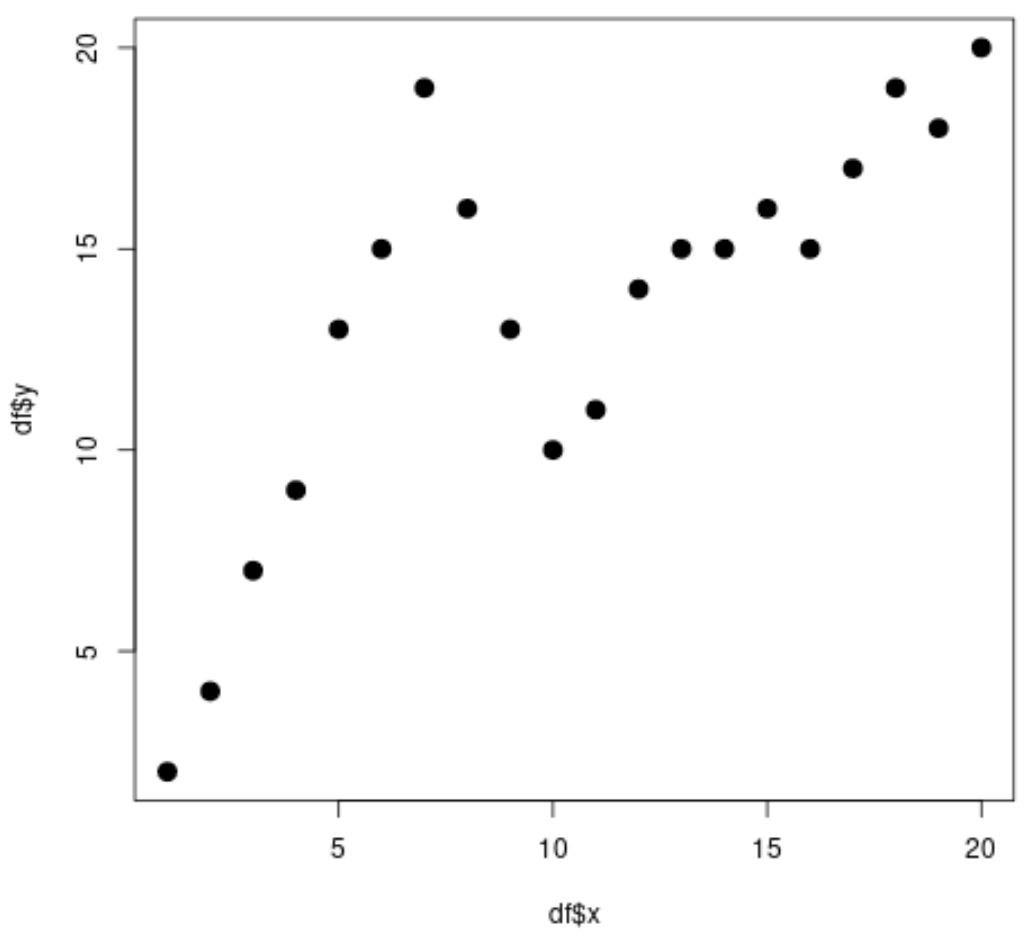
Het is duidelijk dat de relatie tussen x en y niet-lineair is en dat er twee punten of „knooppunten“ lijken te zijn waar het patroon in de gegevens abrupt verandert bij x=7 en x=10.

Stap 2: Pas het eenvoudige lineaire regressiemodel toe

Laten we vervolgens de functie lm() gebruiken om een eenvoudig lineair regressiemodel aan deze gegevensset toe te passen en de regressielijn op het spreidingsdiagram te plotten:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

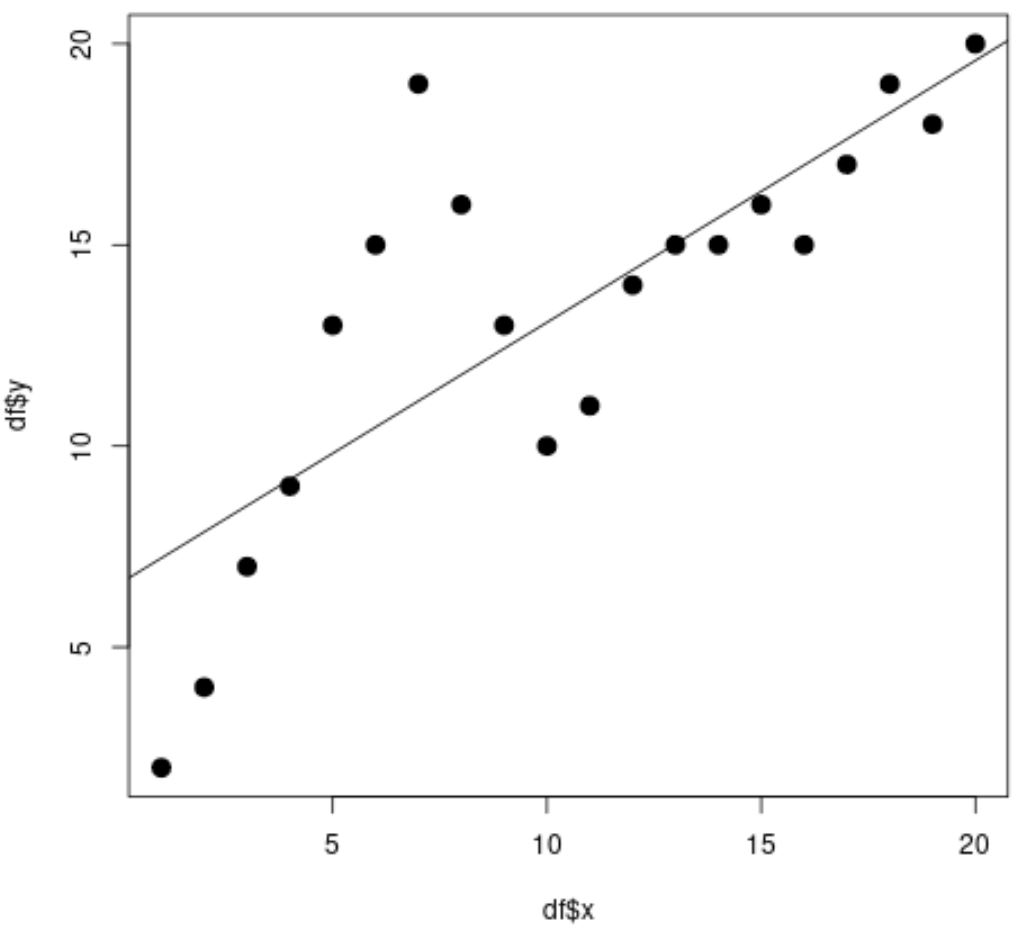
Uit het spreidingsdiagram kunnen we zien dat de eenvoudige lineaire regressielijn niet goed bij de gegevens past.

Uit de modelresultaten kunnen we ook zien dat de aangepaste R-kwadraatwaarde 0,5903 is.

We zullen dit vergelijken met de aangepaste R-kwadraatwaarde van een spline-model.

Stap 3: Pas het spline-regressiemodel aan

Laten we vervolgens de functie bs() uit het splines- pakket gebruiken om een spline-regressiemodel met twee knooppunten te fitten, en vervolgens het gepaste model in de spreidingsdiagram plotten:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

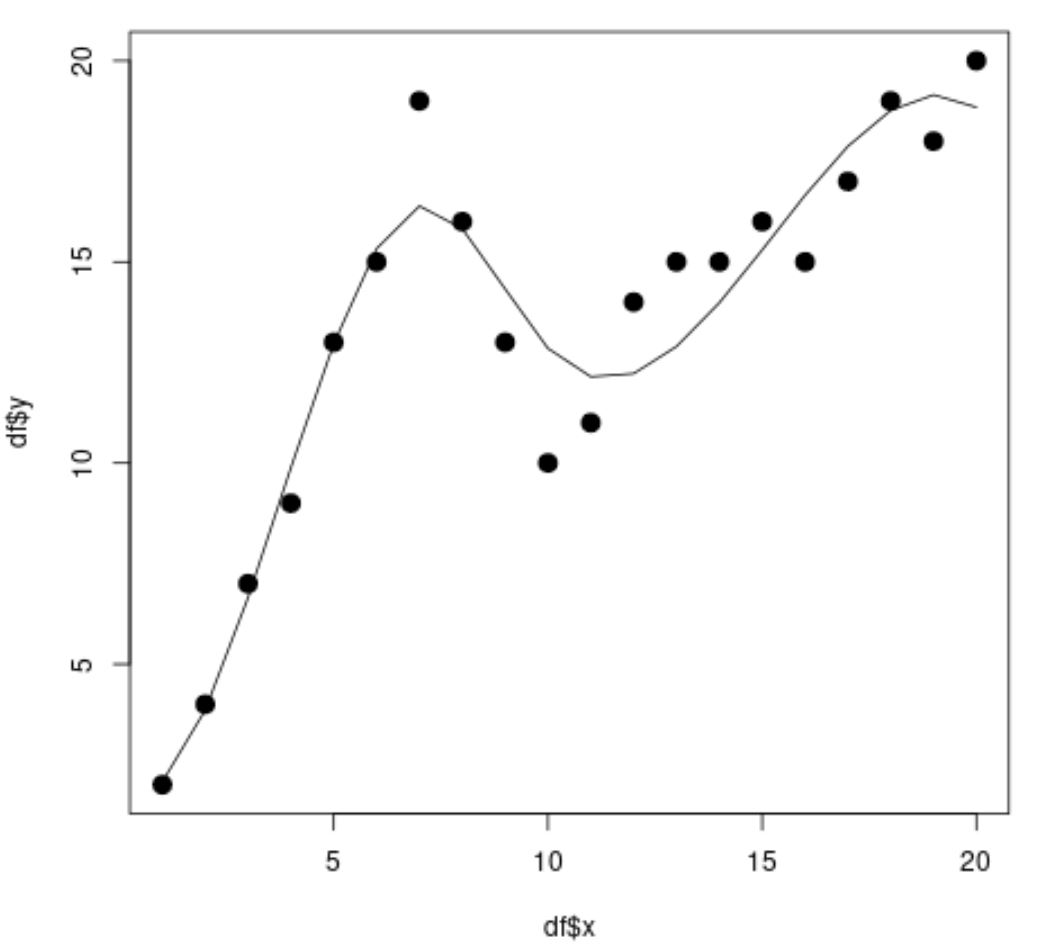
Uit het spreidingsdiagram kunnen we zien dat het spline-regressiemodel de gegevens redelijk goed kan weergeven.

Uit de modelresultaten kunnen we ook zien dat de aangepaste R-kwadraatwaarde 0,8987 is.

De aangepaste R-kwadraatwaarde voor dit model is veel hoger dan het eenvoudige lineaire regressiemodel, wat ons vertelt dat het spline-regressiemodel beter bij de gegevens kan passen.

Merk op dat we er voor dit voorbeeld voor hebben gekozen dat de knooppunten zich op x=7 en x=10 bevinden.

In de praktijk zul je zelf knooppuntlocaties moeten kiezen op basis van waar patronen in de data lijken te veranderen en op basis van jouw domeinexpertise.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe meervoudige lineaire regressie uit te voeren in R
Hoe exponentiële regressie uit te voeren in R
Hoe u een gewogen kleinste kwadratenregressie uitvoert in R