Spreidingsplot
In dit artikel wordt uitgelegd wat spreidingsdiagrammen zijn. Je ontdekt daarom waarvoor een puntenwolk wordt gebruikt, hoe je een puntenwolk maakt, hoe je deze interpreteert en voorbeelden van puntenwolken.
Wat is een puntenwolk?
Scatterplot , of scatterplot , is een soort statistisch diagram waarin een gegevensset van twee variabelen wordt weergegeven op twee cartesiaanse coördinaatassen.
Daarom worden spreidingsdiagrammen gebruikt om de relatie tussen twee statistische variabelen te analyseren.
Scatterplots hebben verschillende namen, zoals correlatiediagram of scatterplot .
Opgemerkt moet worden dat het spreidingsdiagram wordt beschouwd als een van de basisinstrumenten voor kwaliteitscontrole, net zoals het Pareto-diagram, het oorzaak-gevolgdiagram, het stroomdiagram, enz.
Hoe maak je een spreidingsdiagram?
Om een spreidingsdiagram te maken, moet u de volgende stappen volgen:
- Verzamel statistische gegevens van het monster dat u wilt analyseren. Houd er rekening mee dat er, om een spreidingsdiagram te maken, ten minste twee kwantitatieve variabelen moeten zijn.
- Teken de twee assen van het spreidingsdiagram.
- Bepaal de twee statistische variabelen die in een grafiek zullen worden weergegeven.
- Kalibreer de schaal van elke as van de grafiek. Om dit te doen, wordt aanbevolen om eerst het minimum en maximum van elke variabele te vinden en, op basis van deze waarden, elke as te schalen.
- Geef elk paar gegevens op het spreidingsdiagram weer met een punt.
- Analyseer en interpreteer het verkregen spreidingsdiagram.
Voorbeeld van een spreidingsdiagram
Nadat we de definitie van een spreidingsdiagram en de theorie over de creatie ervan hebben gezien, geeft deze sectie een diagram van dit type als voorbeeld.
- In de volgende frequentietabel zijn de wiskunde- en statistiekscores van een steekproef van twintig leerlingen als gegevens verzameld. Zet de dataset in een spreidingsdiagram en analyseer deze.
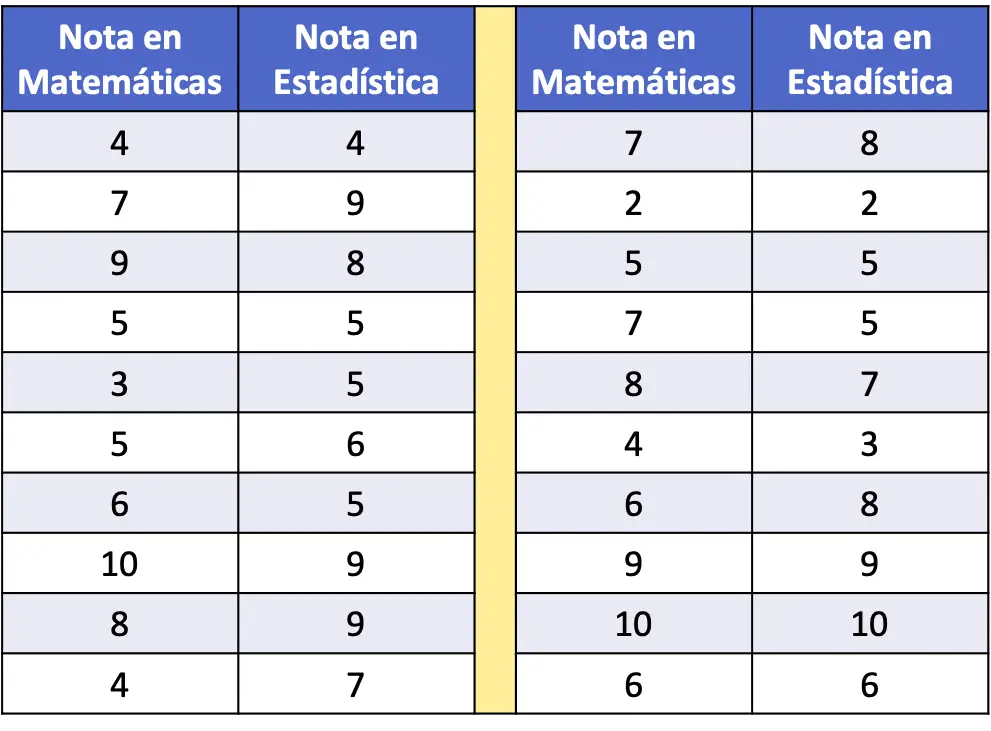
Om de gegevensreeksen in een spreidingsdiagram weer te geven, hoeven we alleen maar twee assen uit te zetten, deze te kalibreren en voor elk paar gegevens een punt in de grafiek uit te zetten. Bedenk dat een punt in een grafiek zich op het snijpunt van de denkbeeldige lijnen bevindt die overeenkomen met elk van de waarden ervan.
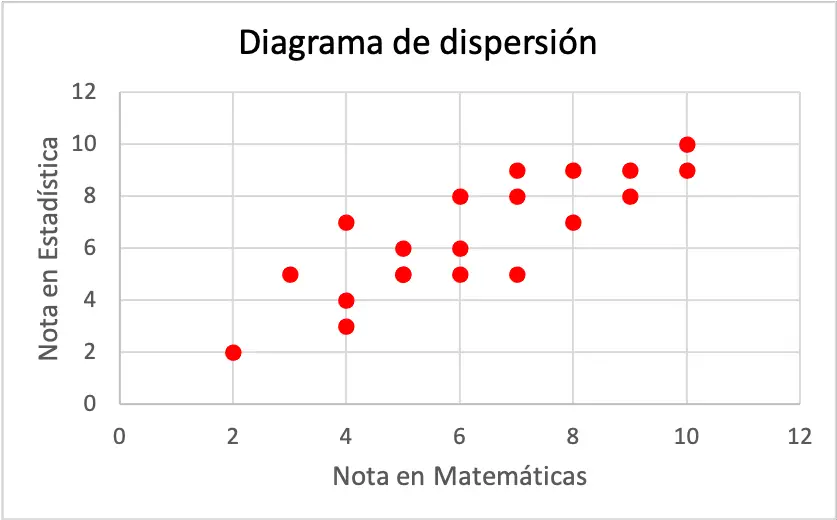
Elke as van het spreidingsdiagram vertegenwoordigt een variabele. Nauwkeuriger gezegd, de horizontale as behoort tot het cijfer behaald in de wiskunde en aan de andere kant komt de verticale as overeen met het cijfer behaald in de statistiek.
Zoals je kunt zien in het spreidingsdiagram, hebben de twee variabelen een positieve correlatie, omdat de ene variabele toeneemt naarmate de andere variabele ook toeneemt. Daarom wordt geconcludeerd dat als een leerling een beter cijfer voor wiskunde haalt, de kans groter is dat hij of zij ook een beter cijfer voor statistiek krijgt, en omgekeerd.
De voorgaande conclusie betekent echter niet dat de ene variabele de oorzaak is van de andere, omdat het behalen van een goed cijfer voor wiskunde niet automatisch een goed cijfer voor statistiek garandeert zonder iets te doen, maar je moet beide vakken studeren. In de volgende paragraaf gaan we dieper in op dit concept.
Het spreidingsdiagram en de correlatie
Vanuit een spreidingsdiagram is het mogelijk om het type correlatie tussen twee variabelen te identificeren:
- Directe correlatie (of positieve correlatie) : de ene variabele neemt toe als de andere ook toeneemt.
- Inverse correlatie (of negatieve correlatie) : wanneer de ene variabele toeneemt, neemt de andere af, en omgekeerd: als de ene variabele afneemt, neemt de andere toe.
- Nulcorrelatie (geen correlatie) : er is geen verband tussen de twee variabelen.
Op dezelfde manier kan de correlatie, ongeacht of de correlatie tussen de twee variabelen direct of omgekeerd is, ook worden geclassificeerd op basis van de sterkte of zwakte van de relatie tussen de twee variabelen.
- Sterke correlatie: de twee variabelen zijn nauw met elkaar verbonden. De punten worden samengebracht op de puntenwolk. Dit maakt het gemakkelijker om de relatie tussen variabelen te identificeren.
- Lage correlatie : er bestaat een relatie tussen de twee variabelen, maar deze is moeilijk te identificeren. Op de puntenwolk liggen de punten ver uit elkaar.

Aan de andere kant kan de correlatie ook numeriek worden berekend met behulp van een formule, waardoor u wiskundig kunt weten hoe nauw verwant twee verschillende variabelen zijn. Om te zien hoe het werkt, klik op de volgende link:
Houd er rekening mee dat zelfs als er een correlatie bestaat tussen twee variabelen, dit niet betekent dat er causaliteit tussen beide variabelen bestaat, dat wil zeggen dat de correlatie tussen twee variabelen niet betekent dat de verandering in de ene variabele de oorzaak is van de verandering in de andere. variabel.
Dus, net als in het spreidingsdiagram in de vorige sectie, betekent het behalen van een goed cijfer voor wiskunde, ook al is er een positieve correlatie tussen het cijfer voor wiskunde en het cijfer voor statistiek, niet dat je een goed cijfer voor statistiek krijgt, want als je alleen maar wiskunde studeert, zul je zeker falen. bij statistieken. Daarom zijn de twee variabelen gerelateerd, maar ze zijn geen oorzaak en gevolg.
Voor meer informatie kunt u doorgaan met het volgende bericht:
Voor- en nadelen van puntenwolk
Vanwege de kenmerken van het spreidingsdiagram heeft dit type statistische grafiek voor- en nadelen.
Voordeel:
- Het is vrij eenvoudig om een reeks gegevens weer te geven in een spreidingsdiagram.
- Met het spreidingsdiagram kunt u de relatie tussen twee variabelen visueel analyseren, waardoor het gemakkelijker wordt om conclusies te trekken.
- Scatterplots kunnen ook worden gebruikt in een diepgaand statistisch onderzoek als voorlopige gegevensverkenning.
Nadelen:
- Dit soort diagrammen zijn niet bruikbaar voor het weergeven van kwalitatieve variabelen.
- Het interpreteren van een spreidingsdiagram kan leiden tot een foutieve conclusie van oorzaak en gevolg tussen twee variabelen.
- Met spreidingsdiagrammen kunt u de relatie tussen meer dan twee variabelen niet analyseren.