Hoe u eenvoudige lineaire regressie uitvoert in spss

Eenvoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een voorspellende variabele en een responsvariabele te begrijpen.

In deze tutorial wordt uitgelegd hoe u een eenvoudige lineaire regressie uitvoert in SPSS.

Voorbeeld: eenvoudige lineaire regressie in SPSS

Laten we zeggen dat we de volgende dataset hebben die het aantal gestudeerde uren en het behaalde examencijfer van 20 studenten toont:

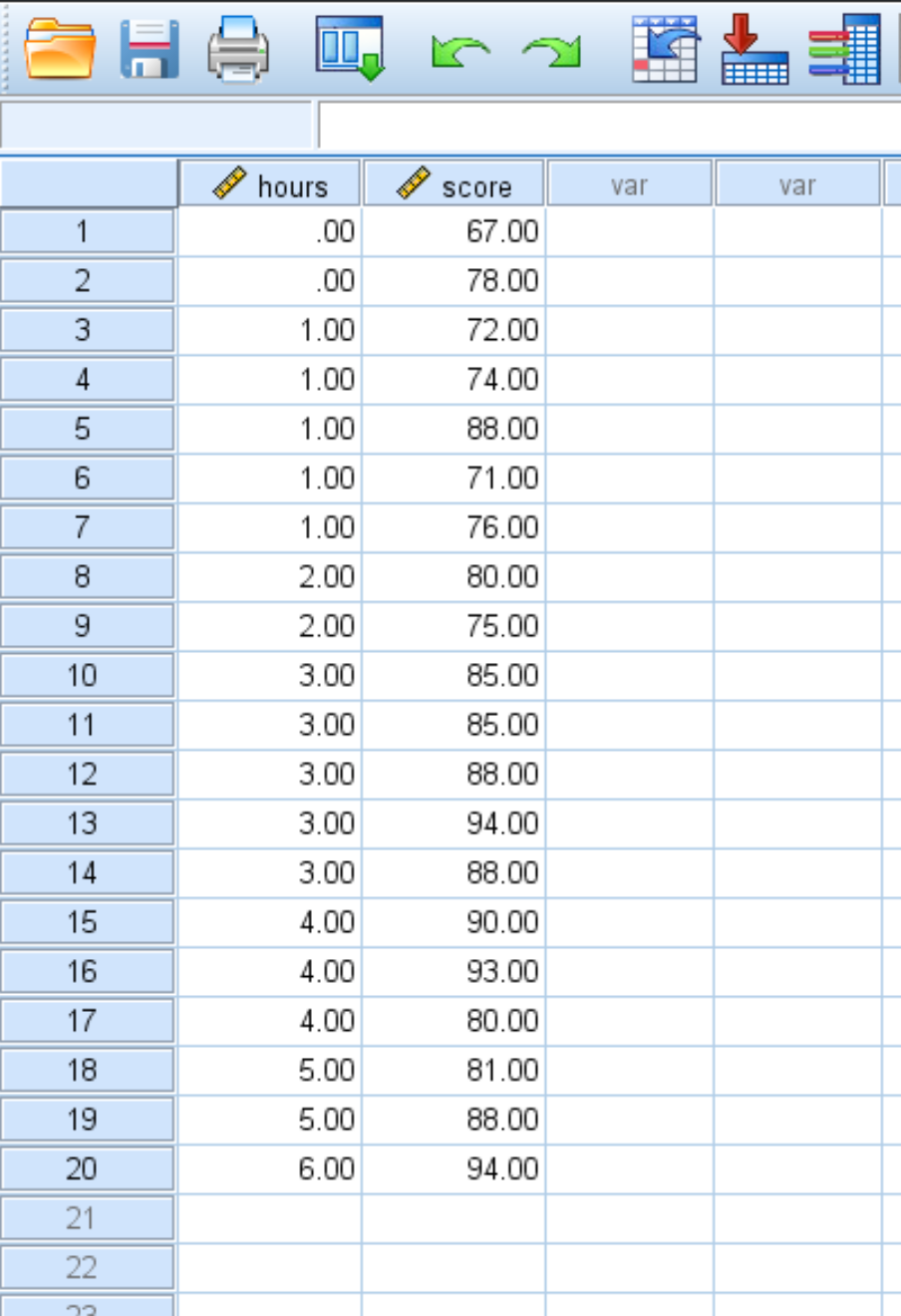
Gebruik de volgende stappen om een eenvoudige lineaire regressie uit te voeren op deze dataset om de relatie tussen bestudeerde uren en examenscore te kwantificeren:

Stap 1: Visualiseer de gegevens.

Eerst zullen we een spreidingsdiagram maken om de relatie tussen uren en score te visualiseren om ervoor te zorgen dat de relatie tussen de twee variabelen lineair lijkt. Anders zal eenvoudige lineaire regressie geen geschikte techniek zijn.

Klik op het tabblad Grafieken en klik vervolgens op Grafiekbouwer :

Klik en sleep vanuit het menu Kiezen uit Scatter/Dot naar het hoofdbewerkingsvenster. Sleep vervolgens de variabele tijden naar de x-as en de score naar de y-as.

Zodra u op OK klikt, verschijnt het volgende spreidingsdiagram:

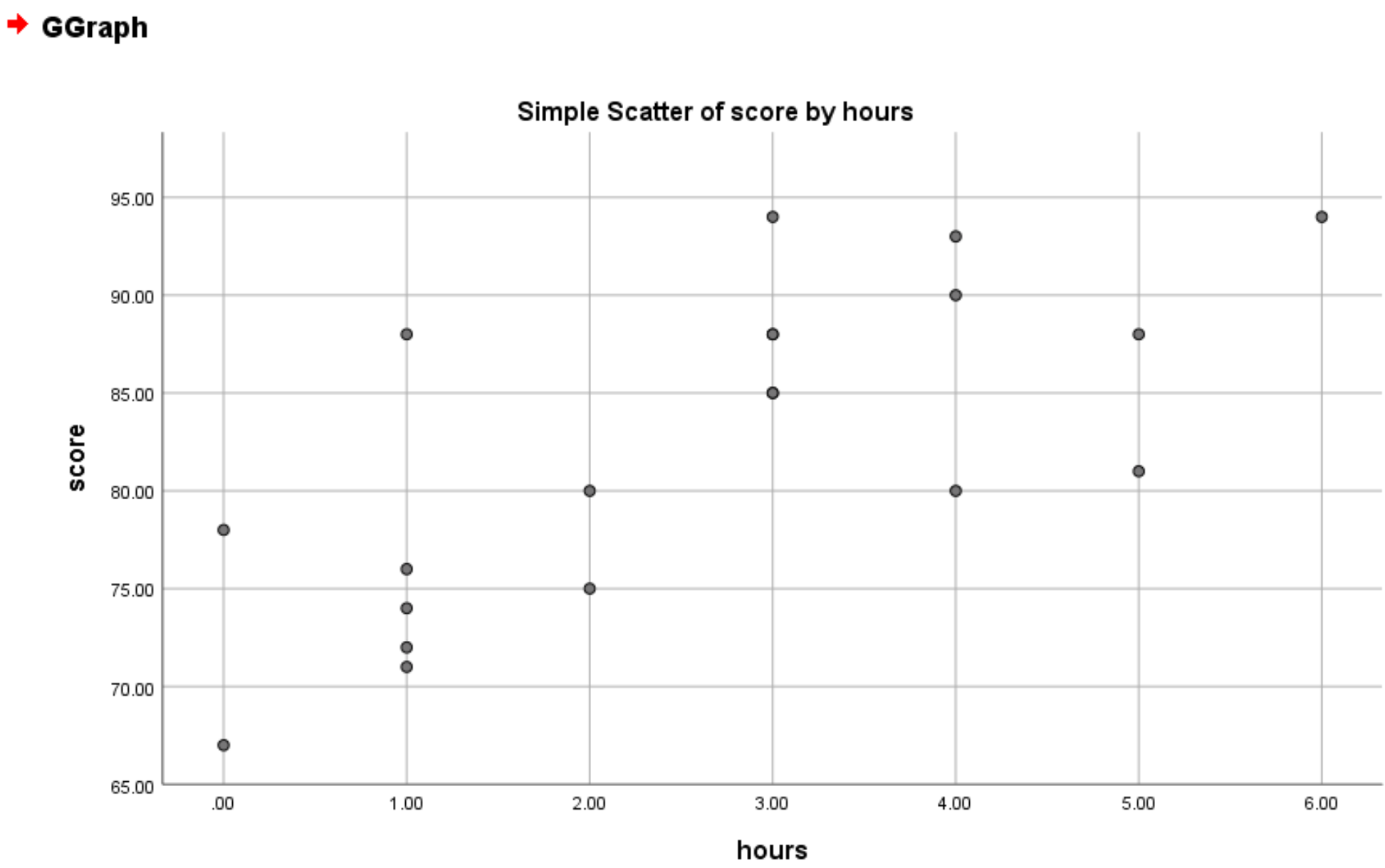
Uit de grafiek kunnen we zien dat er een positief lineair verband bestaat tussen uren en score. Over het algemeen scoren studenten die meer uren studeren doorgaans hoger.

Omdat er een duidelijk lineair verband bestaat tussen de twee variabelen, gaan we over tot het inpassen van een eenvoudig lineair regressiemodel in de dataset.

Stap 2: Pas een eenvoudig lineair regressiemodel toe.

Klik op het tabblad Analyseren , vervolgens op Regressie en vervolgens op Lineair :

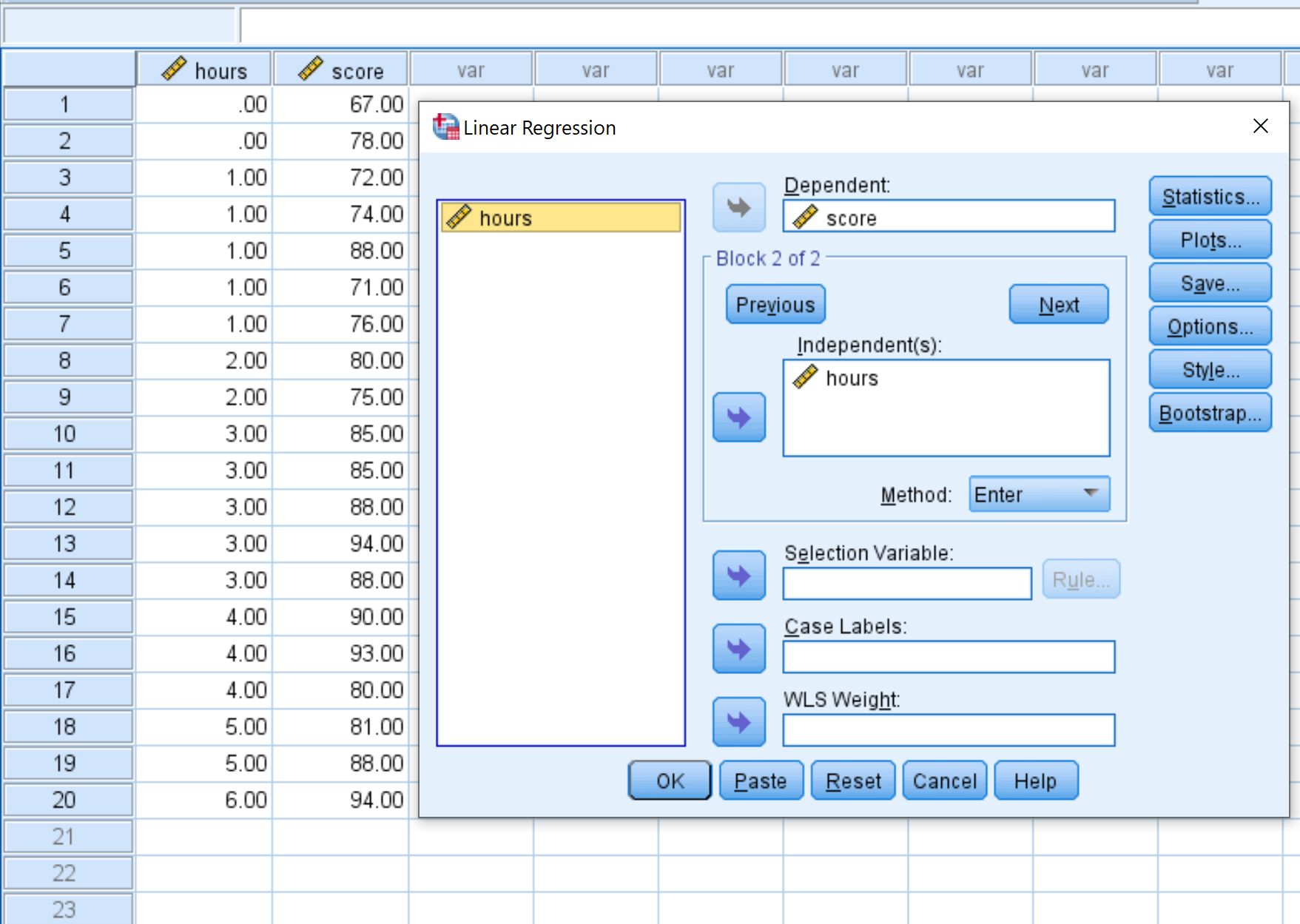
In het nieuwe venster dat verschijnt, sleept u de variabele score naar het vak met de naam Afhankelijk en sleept u de uren naar het vak met de naam Onafhankelijk. Klik vervolgens op OK .

Stap 3: Interpreteer de resultaten.

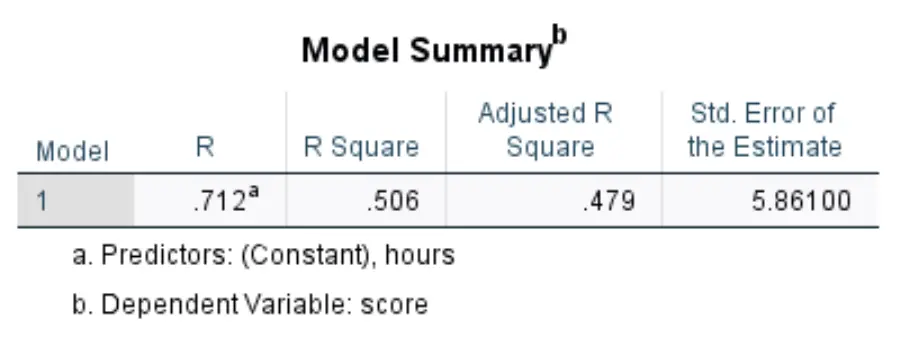
Zodra u op OK klikt, verschijnen de eenvoudige lineaire regressieresultaten. De eerste tabel die ons interesseert is de tabel met de titel Modelsamenvatting :

Zo interpreteert u de meest relevante cijfers in deze tabel:

• R-kwadraat: Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabele. In dit voorbeeld kan 50,6% van de variatie in examenscores worden verklaard door gestudeerde uren.
• Standaard. Schattingsfout: de standaardfout is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 5.861 eenheden af van de regressielijn.

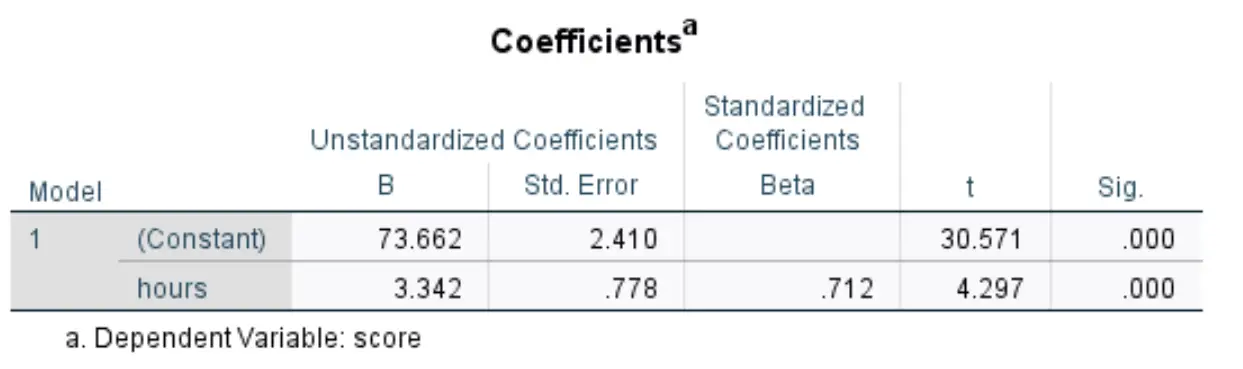
De volgende tabel die ons interesseert, heeft de titel Coëfficiënten :

Zo interpreteert u de meest relevante cijfers in deze tabel:

• Niet-gestandaardiseerde B (constant) : dit vertelt ons de gemiddelde waarde van deresponsvariabele wanneer de voorspellende variabele nul is. In dit voorbeeld is de gemiddelde examenscore 73,662 wanneer het aantal bestudeerde uren nul is.
• B niet-gestandaardiseerd (uren): dit vertelt ons de gemiddelde verandering in de responsvariabele die gepaard gaat met een toename van één eenheid in de voorspellende variabele. In dit voorbeeld gaat elk extra uur dat je studeerde gepaard met een gemiddelde stijging van de examenscore met 3.342 .
• Sig (uren): Dit is de p-waarde die is gekoppeld aan de teststatistiek gedurende uren. In dit geval kunnen we, aangezien deze waarde kleiner is dan 0,05, concluderen dat de voorspellende variabele uren statistisch significant is.

Ten slotte kunnen we een regressievergelijking vormen met behulp van de waarden van constante en uren . In dit geval zou de vergelijking zijn:

Geschatte examenscore = 73.662 + 3.342*(uren)

We kunnen deze vergelijking gebruiken om de geschatte examenscore van een student te vinden, op basis van het aantal gestudeerde uren.

Een student die bijvoorbeeld 3 uur studeert, moet een examenscore van 83,688 behalen:

Geschatte examenscore = 73.662 + 3.342*(3) = 83.688

Stap 4: Rapporteer de resultaten.

Ten slotte willen we de resultaten van onze eenvoudige lineaire regressie samenvatten. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een eenvoudige lineaire regressie uitgevoerd om de relatie tussen het aantal gestudeerde uren en het examencijfer te kwantificeren. Voor de analyse is gebruik gemaakt van een steekproef van twintig studenten.

Uit de resultaten bleek dat er een statistisch significante relatie bestond tussen het aantal gestudeerde uren en het examencijfer (t = 4,297, p < 0,000) en dat het aantal gestudeerde uren verantwoordelijk was voor 50,6% van de verklaarde variabiliteit in het examencijfer. het examen.

De regressievergelijking bleek:

Geschatte examenscore = 73.662 + 3.342*(uren)

Elk extra uur studeren gaat gepaard met een gemiddelde stijging van de examenscore met 3.342 .

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in SPSS kunt uitvoeren:

Hoe u meervoudige lineaire regressie uitvoert in SPSS
Hoe kwadratische regressie uit te voeren in SPSS
Hoe logistische regressie uit te voeren in SPSS