Hoe kwadratische regressie uit te voeren in spss

Wanneer twee variabelen een lineair verband hebben, kunt u vaak eenvoudige lineaire regressie gebruiken om hun verband te kwantificeren.

Eenvoudige lineaire regressie werkt echter niet goed als twee variabelen een niet-lineair verband hebben. In deze gevallen kunt u kwadratische regressie gebruiken.

In deze tutorial wordt uitgelegd hoe u kwadratische regressie uitvoert in SPSS.

Voorbeeld: kwadratische regressie in SPSS

Stel dat we de relatie tussen het aantal gewerkte uren en geluk willen begrijpen. We hebben de volgende gegevens over het aantal gewerkte uren per week en het gerapporteerde geluksniveau (op een schaal van 0 tot 100) voor 16 verschillende mensen:

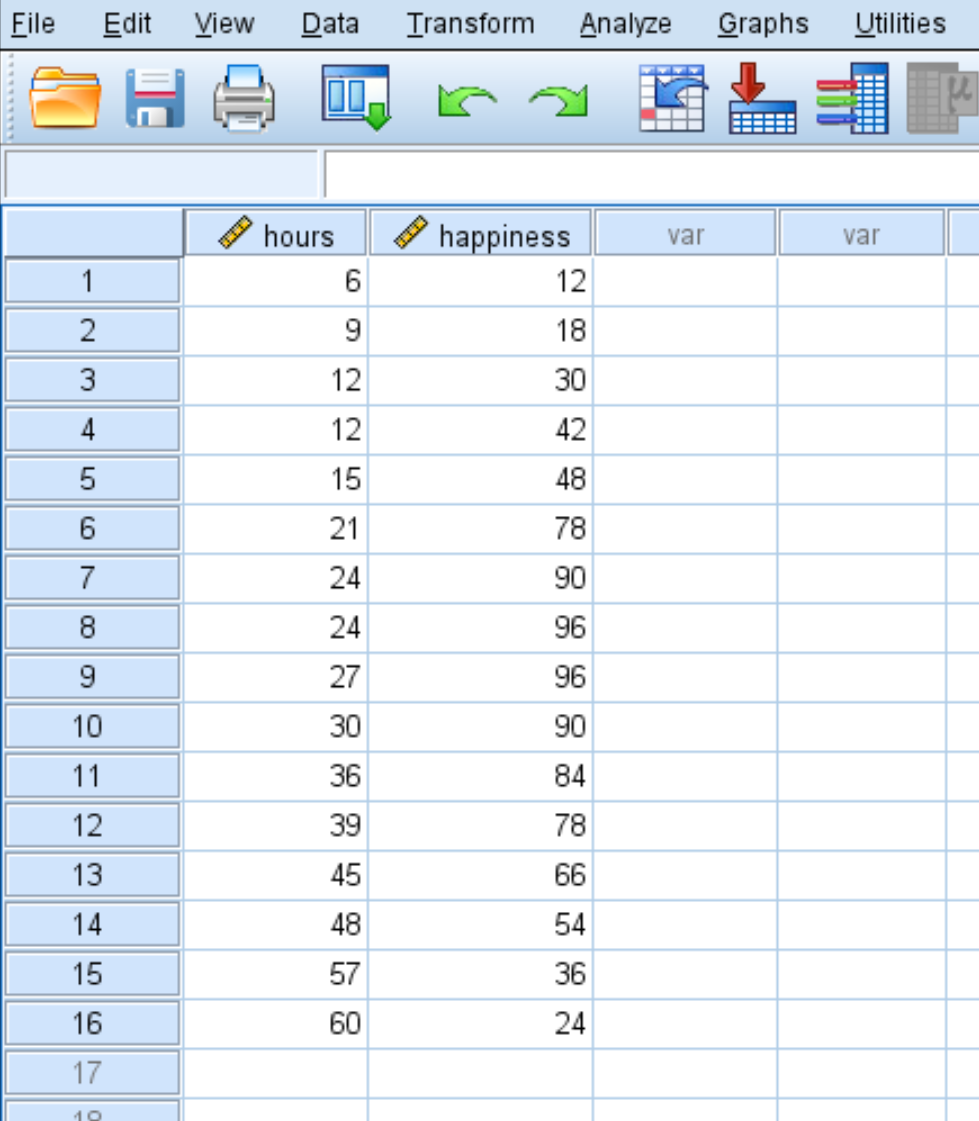
Gebruik de volgende stappen om kwadratische regressie uit te voeren in SPSS.

Stap 1: Visualiseer de gegevens.

Voordat we een kwadratische regressie uitvoeren, maken we een spreidingsdiagram om de relatie tussen gewerkte uren en geluk te visualiseren, om te verifiëren dat de twee variabelen daadwerkelijk een kwadratische relatie hebben.

Klik op het tabblad Grafieken en klik vervolgens op Grafiekbouwer :

In het nieuwe venster dat verschijnt, kiest u Scatter/Dot in de lijst Kiezen uit . Sleep vervolgens het diagram met de naam Simple Scatter naar het hoofdbewerkingsvenster. Sleep variabele uren op de x-as en geluk op de y-as. Klik vervolgens op OK .

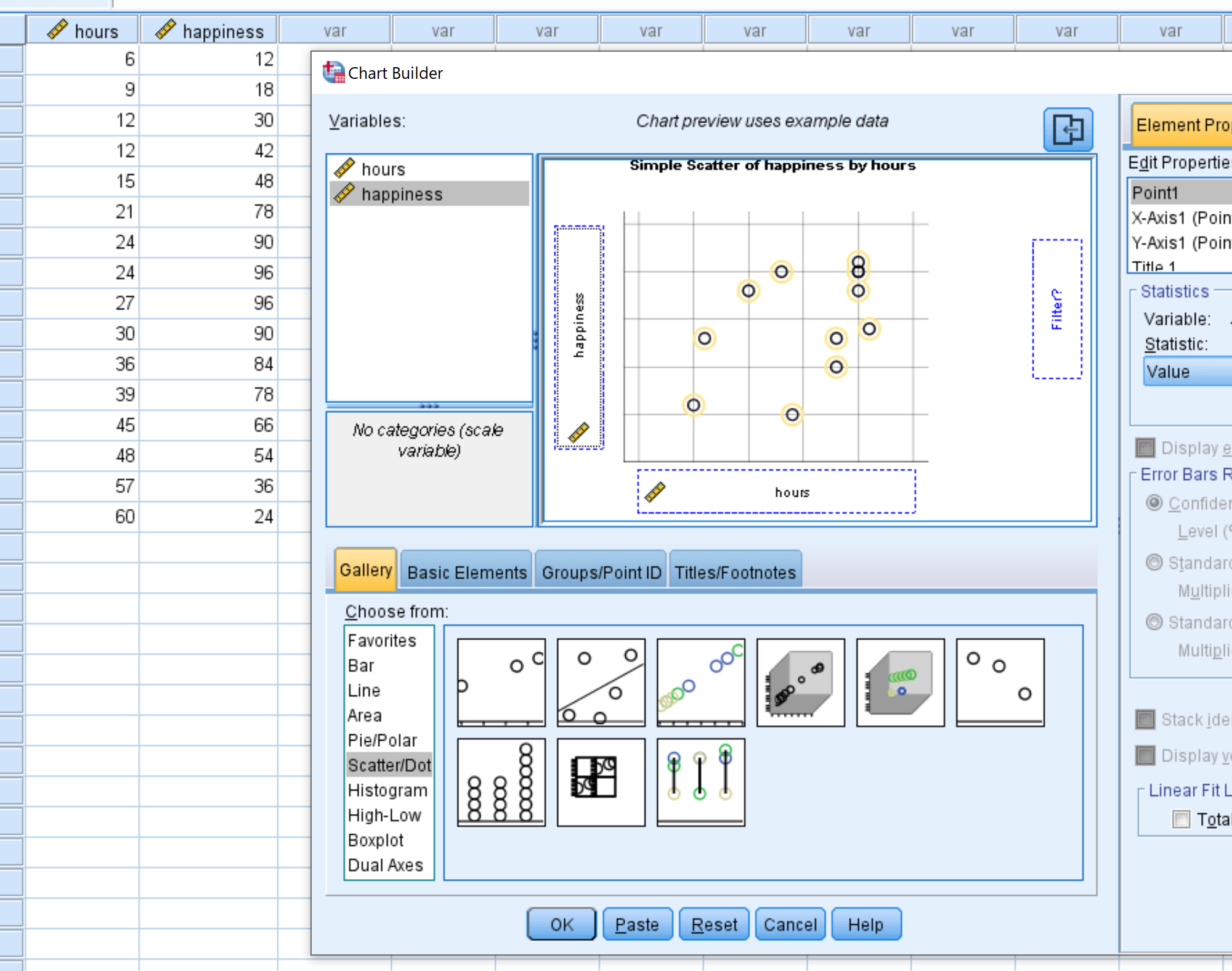
Het volgende spreidingsdiagram verschijnt:

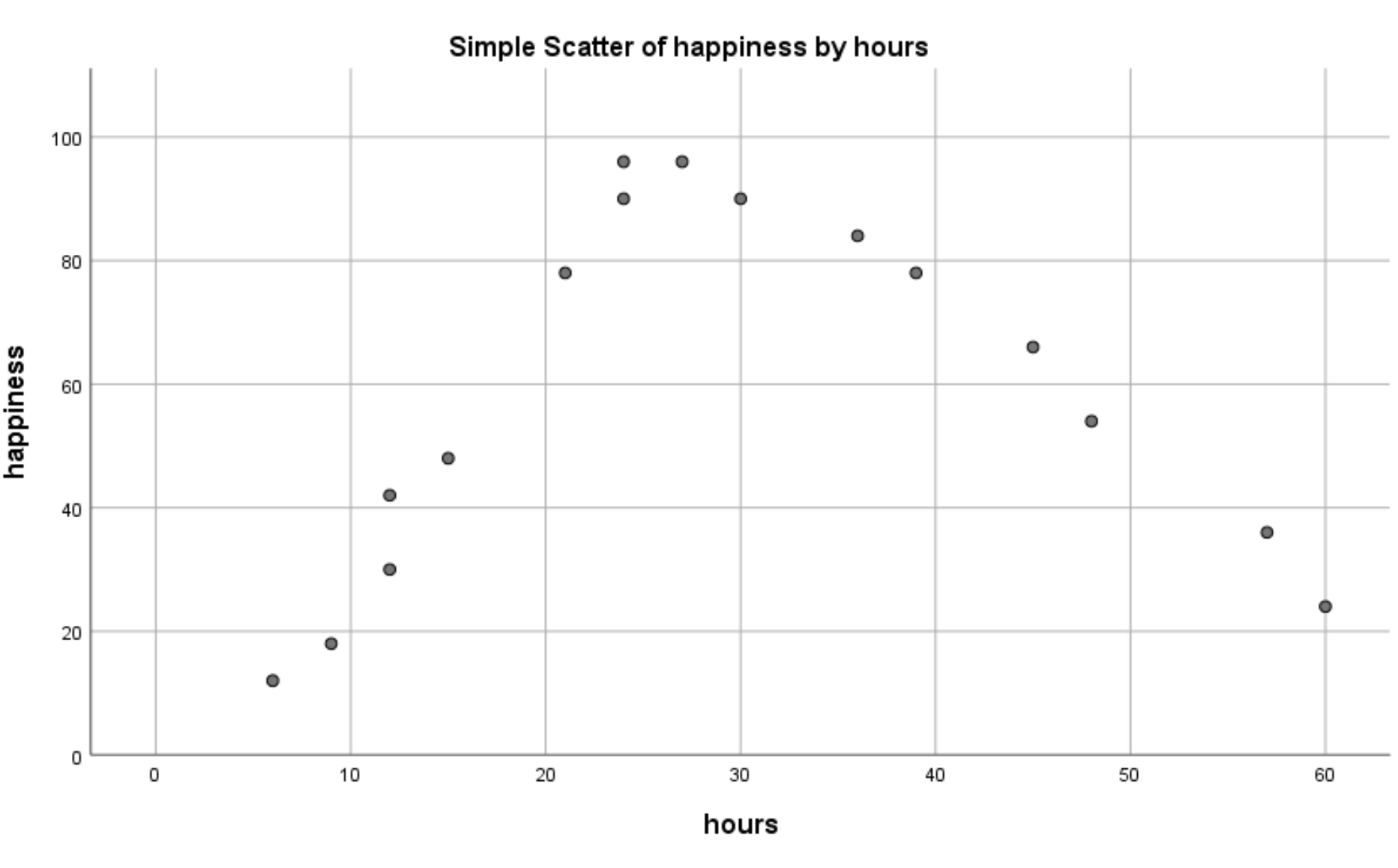
We kunnen duidelijk zien dat er een niet-lineaire relatie bestaat tussen gewerkte uren en geluk. Dit vertelt ons dat kwadratische regressie een geschikte techniek is om in deze situatie te gebruiken.

Stap 2: Maak een nieuwe variabele.

Voordat we een kwadratische regressie kunnen uitvoeren, moeten we een voorspellende variabele voor uren ² creëren.

Klik op het tabblad Transformatie en klik vervolgens op Variabele berekenen :

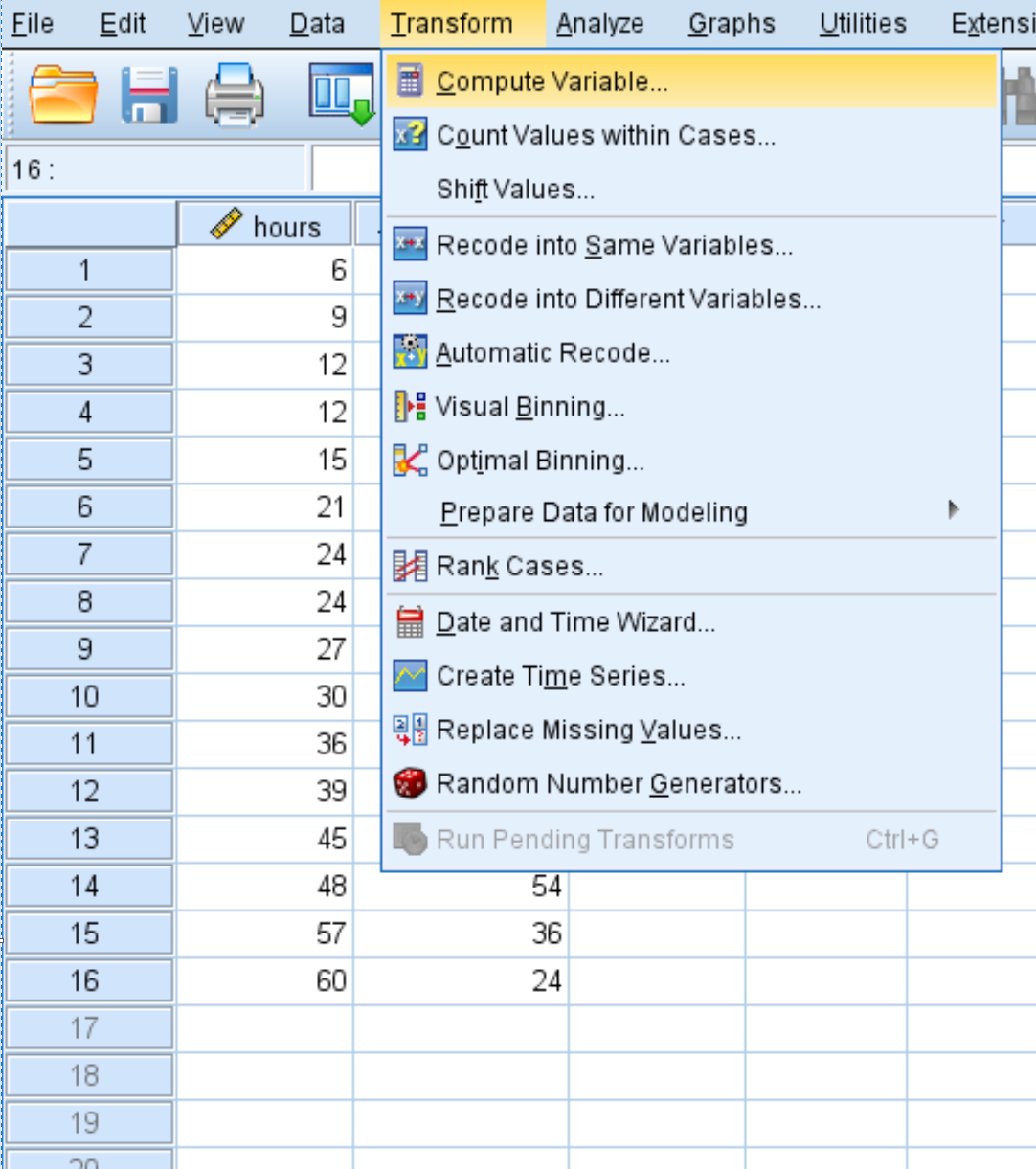
In het nieuwe venster dat verschijnt, geeft u de doelvariabele hours2 een naam en stelt u deze in op hours*hour :

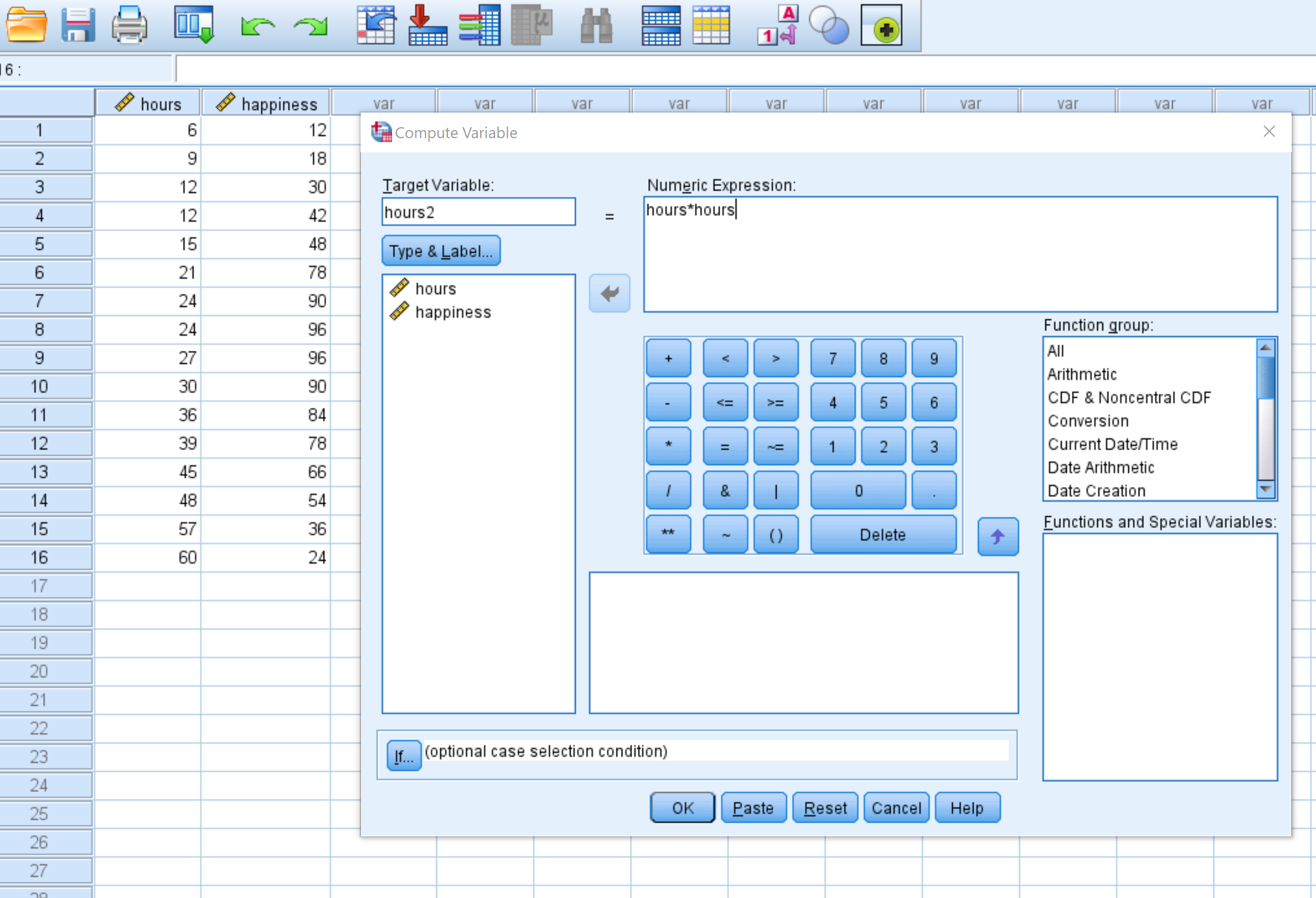
Zodra u op OK klikt, verschijnt de variabele hours2 in een nieuwe kolom:

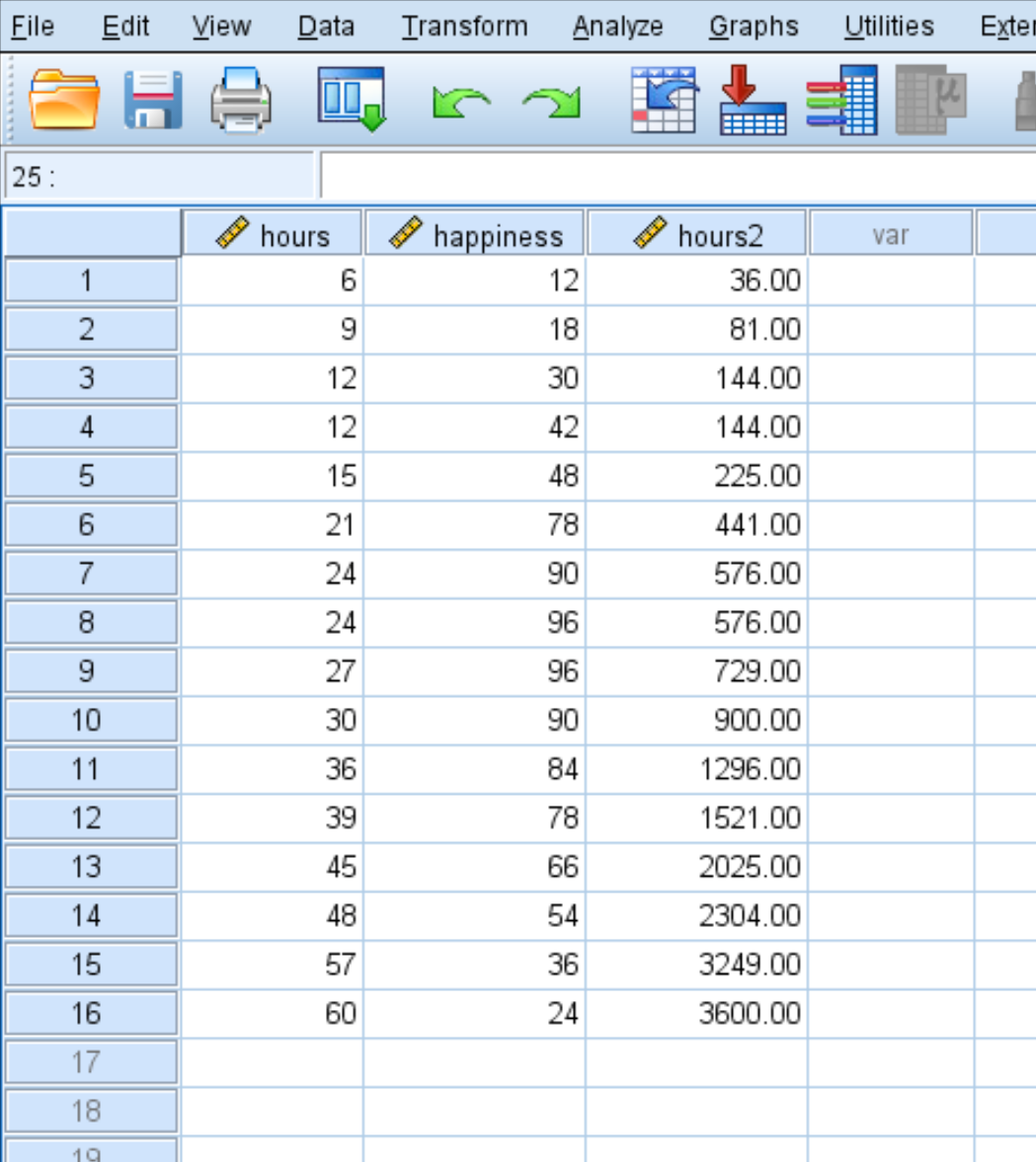
Stap 3: Voer kwadratische regressie uit.

Vervolgens zullen we een kwadratische regressie uitvoeren. Klik op het tabblad Analyseren , vervolgens op Regressie en vervolgens op Lineair :

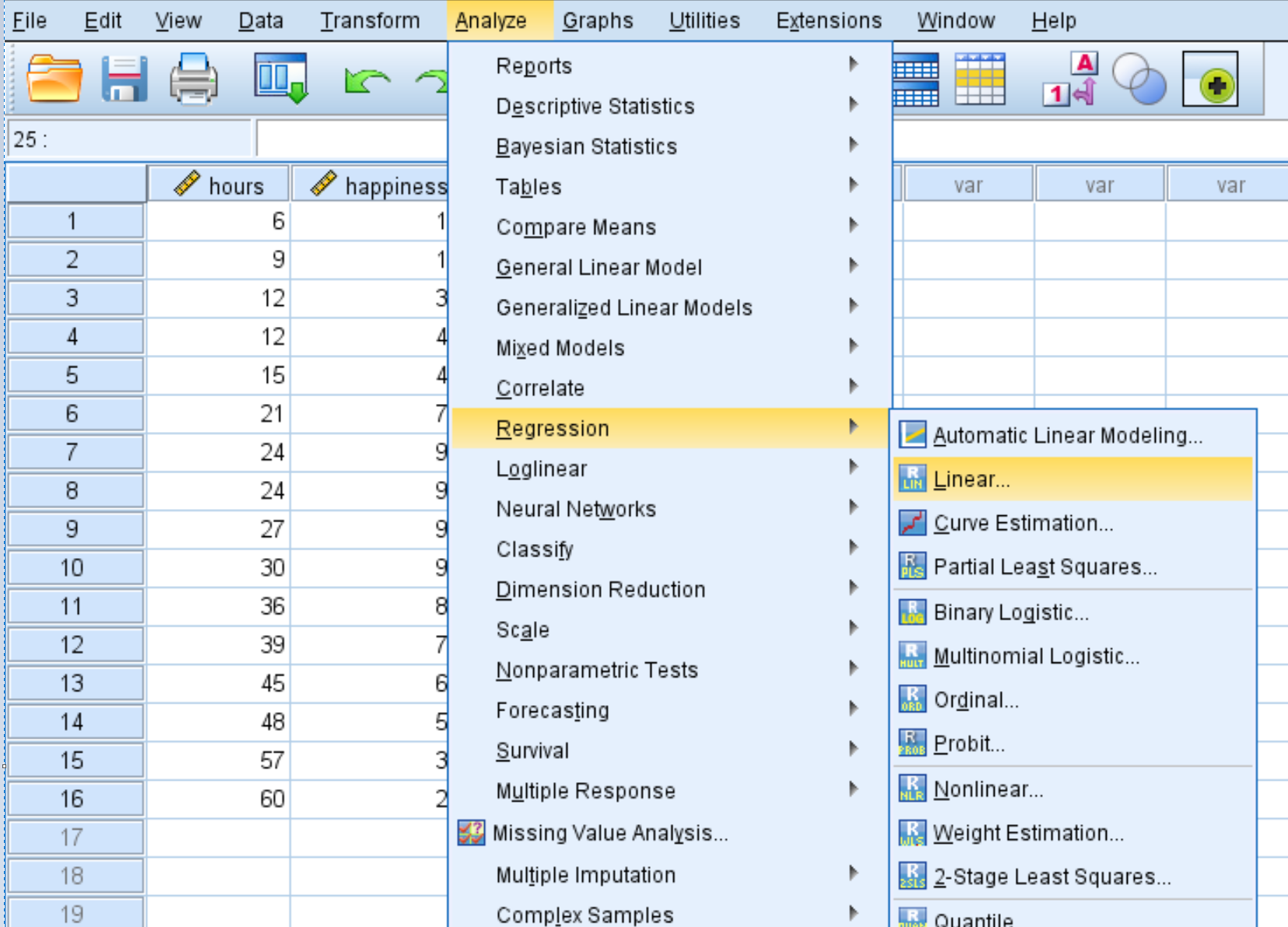
In het nieuwe venster dat verschijnt, sleep je het geluk naar het vak met het label Dependent. Sleep Uren en Uren2 naar het vak met het label Onafhankelijk(en). Klik vervolgens op OK .

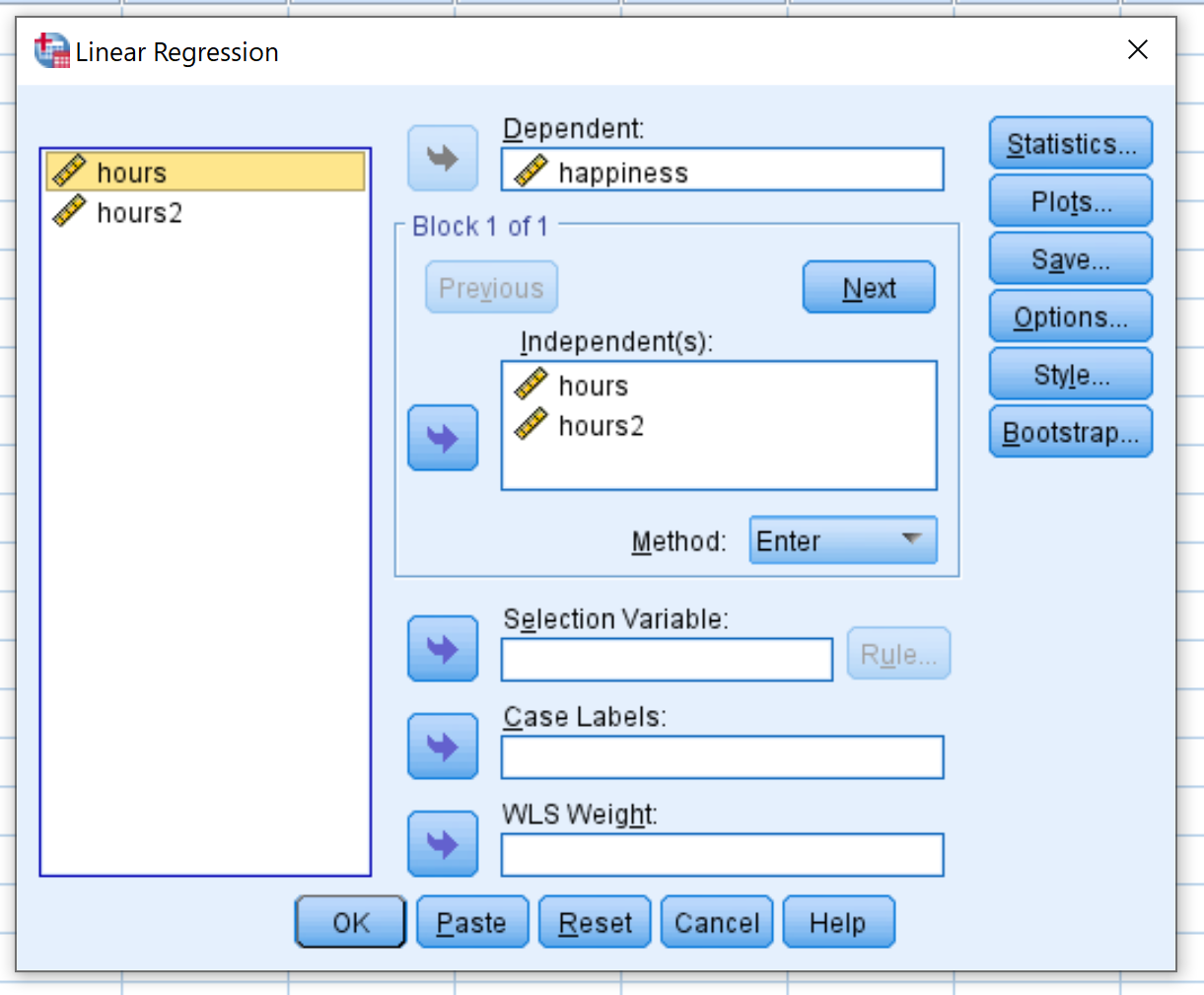
Stap 4: Interpreteer de resultaten.

Zodra u op OK klikt, verschijnen de kwadratische regressieresultaten in een nieuw venster.

De eerste tabel die ons interesseert heet Modelsamenvatting :

Zo interpreteert u de meest relevante cijfers in deze tabel:

• R-kwadraat: Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabelen. In dit voorbeeld kan 90,9% van de variatie in geluk worden verklaard door de uren en uren ² -variabelen.
• Standaard. Schattingsfout: de standaardfout is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 9.519 eenheden af van de regressielijn.

De volgende tabel die ons interesseert heet ANOVA :

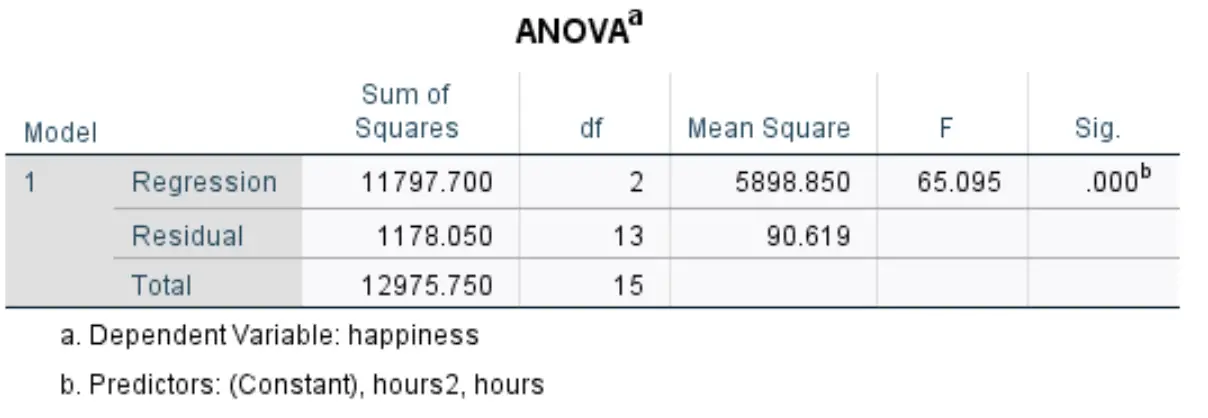
Zo interpreteert u de meest relevante cijfers in deze tabel:

• F: Dit is de algemene F-statistiek voor het regressiemodel, berekend als Mean Square Regression / Mean Square Residual.
• Sig: Dit is de p-waarde die is gekoppeld aan de algehele F-statistiek. Dit vertelt ons of het regressiemodel als geheel statistisch significant is of niet. In dit geval is de p-waarde gelijk aan 0,000, wat aangeeft dat de verklarende variabelen uren en uur ² samen een statistisch significant verband hebben met het examenresultaat.

De volgende tabel die ons interesseert, heeft de titel Coëfficiënten :

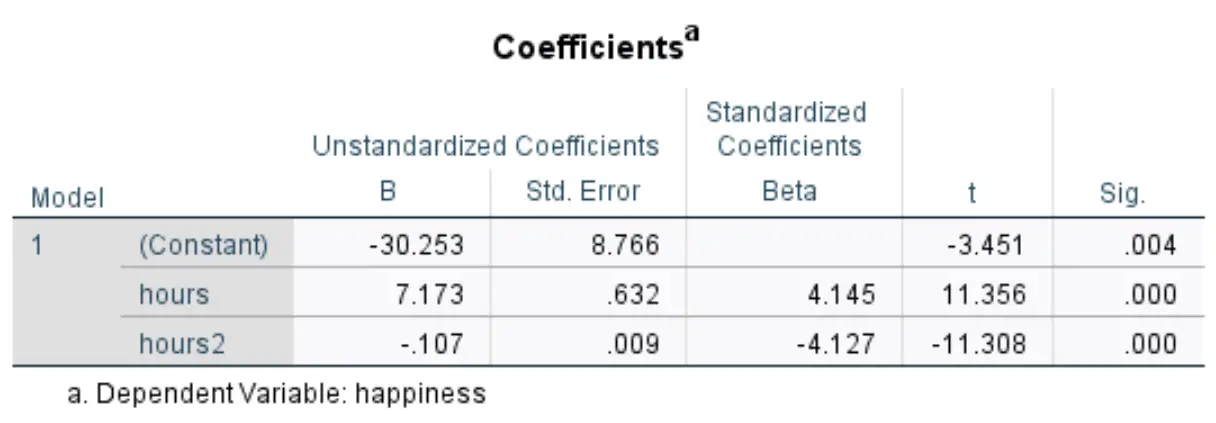
We kunnen de waarden in de kolom Niet-gestandaardiseerd B gebruiken om de geschatte regressievergelijking voor deze dataset te vormen:

Geschat geluksniveau = -30,253 + 7,173*(uren) – 0,107*(uren ² )

We kunnen deze vergelijking gebruiken om het geschatte geluksniveau van een individu te vinden op basis van het aantal gewerkte uren per week. Een persoon die bijvoorbeeld 60 uur per week werkt, zou een geluksniveau van 14,97 moeten hebben:

Geschat geluksniveau = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

Omgekeerd zou iemand die 30 uur per week werkt een geluksniveau van 88,65 moeten hebben:

Geschat geluksniveau = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Stap 5: Rapporteer de resultaten.

Ten slotte willen we de resultaten van onze kwadratische regressie rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een kwadratische regressie uitgevoerd om de relatie te kwantificeren tussen het aantal uren dat iemand werkte en het overeenkomstige geluksniveau (gemeten van 0 tot 100). Voor de analyse is gebruik gemaakt van een steekproef van 16 personen.

Uit de resultaten bleek dat er een statistisch significante relatie bestond tussen de verklarende variabelen uren en uur ² en de responsvariabele geluk (F(2, 13) = 65,095, p < 0,000).

Samen waren deze twee verklarende variabelen verantwoordelijk voor 90,9% van de variabiliteit in geluk.

De regressievergelijking bleek:

Geschat geluksniveau = -30,253 + 7,173 (uren) – 0,107 ( ² uur)