Hoe u meervoudige lineaire regressie uitvoert in spss

Meervoudige lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen twee of meer verklarende variabelen en een responsvariabele te begrijpen.

In deze tutorial wordt uitgelegd hoe u meervoudige lineaire regressie uitvoert in SPSS.

Voorbeeld: meervoudige lineaire regressie in SPSS

Stel dat we willen weten of het aantal studie-uren en het aantal afgelegde oefenexamens invloed hebben op het cijfer dat een student op een bepaald examen krijgt. Om dit te onderzoeken, kunnen we meerdere lineaire regressies uitvoeren met behulp van de volgende variabelen:

Verklarende variabelen:

• Uren gestudeerd
• Voorbereidende examens geslaagd

Responsvariabele:

• Examenresultaat

Gebruik de volgende stappen om deze meervoudige lineaire regressie uit te voeren in SPSS.

Stap 1: Voer de gegevens in.

Vul voor het aantal gestudeerde uren, afgelegde voorbereidende examens en ontvangen examenresultaten van 20 studenten de volgende gegevens in:

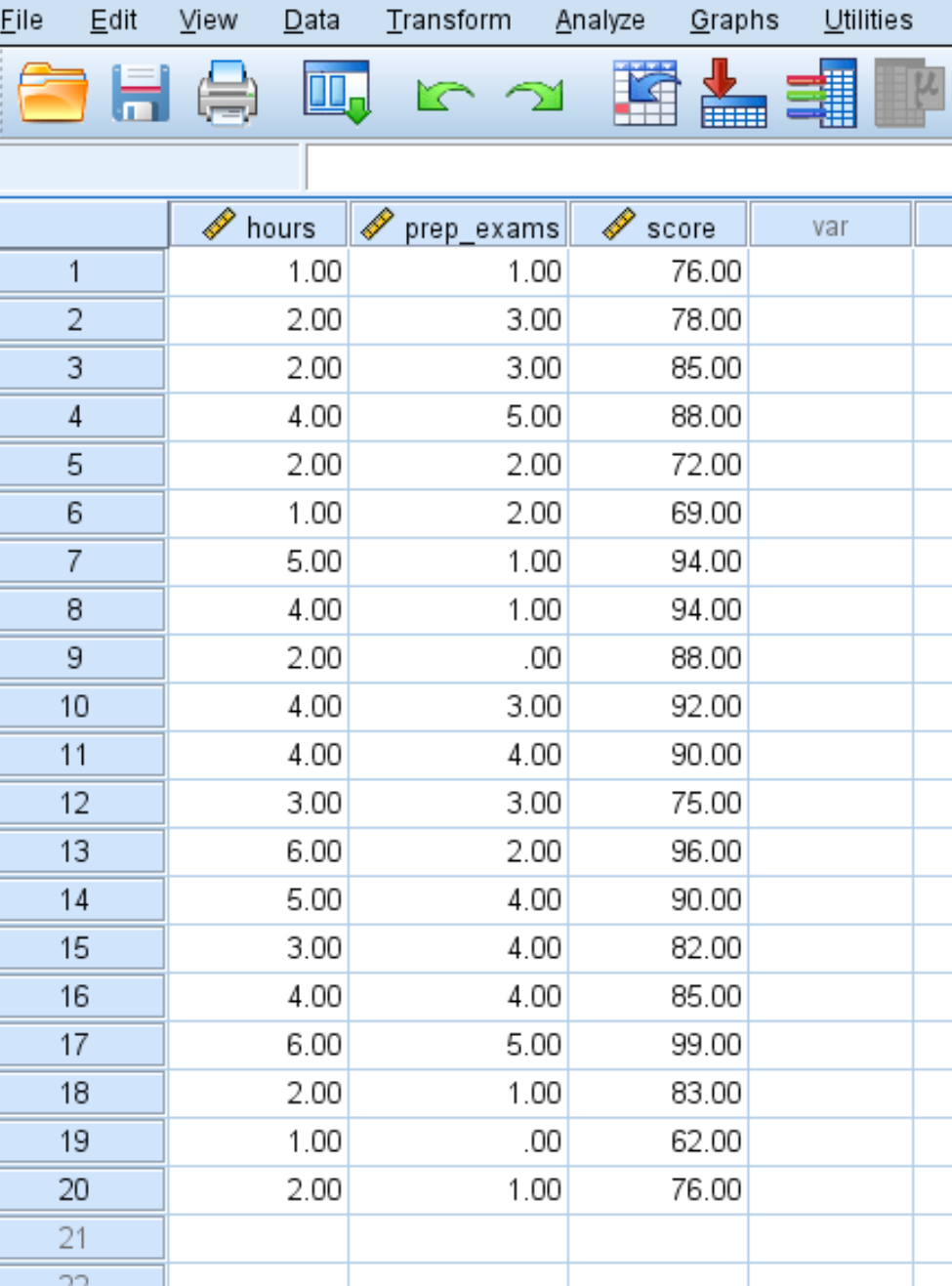
Stap 2: Voer meerdere lineaire regressie uit.

Klik op het tabblad Analyseren , vervolgens op Regressie en vervolgens op Lineair :

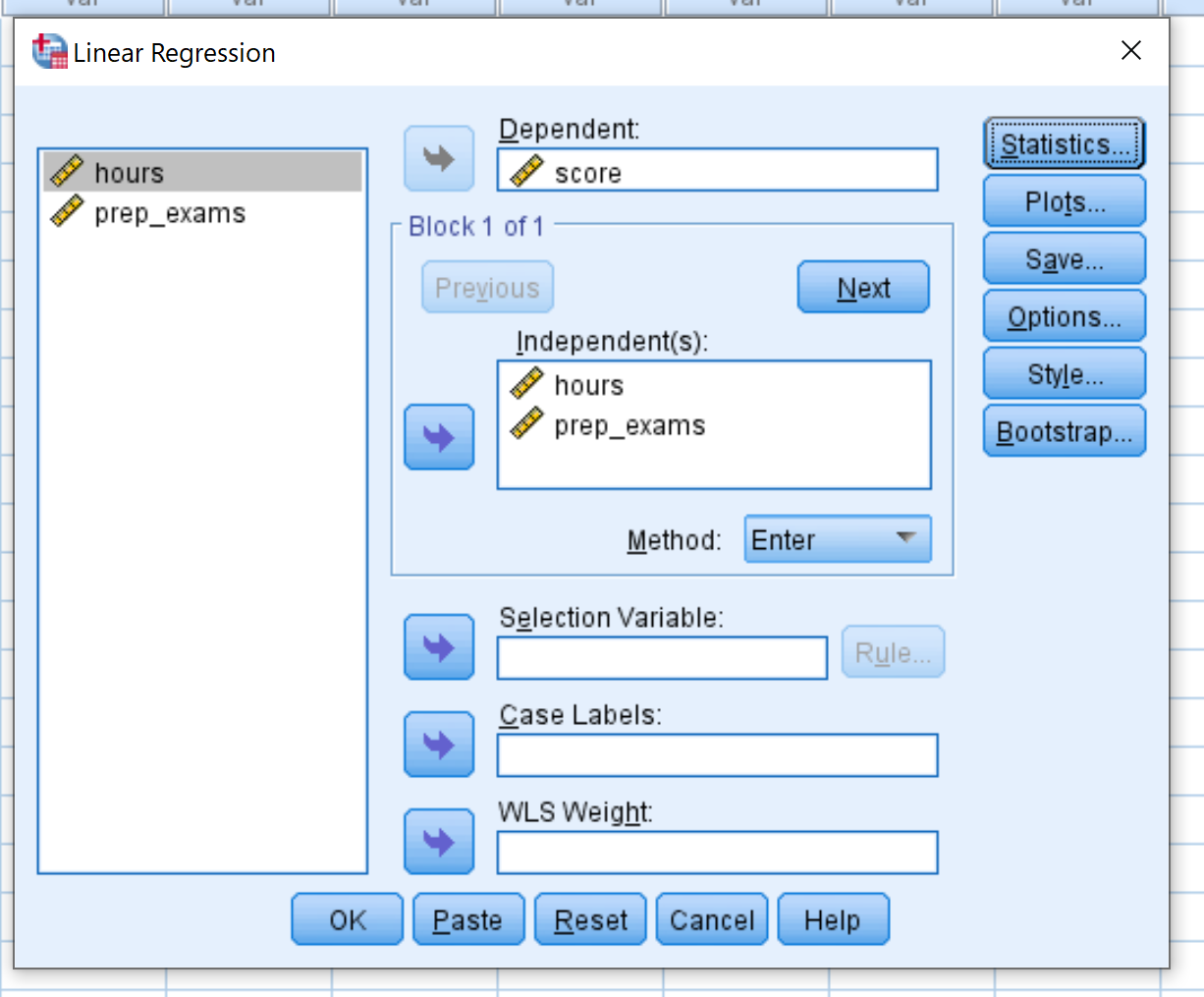
Sleep de variabele score naar het vak met het label Afhankelijk. Sleep de variabelen uren en prep_exams naar het vak met de naam Independent(s). Klik vervolgens op OK .

Stap 3: Interpreteer het resultaat.

Zodra u op OK klikt, verschijnen de resultaten van de meervoudige lineaire regressie in een nieuw venster.

De eerste tabel die ons interesseert heet Modelsamenvatting :

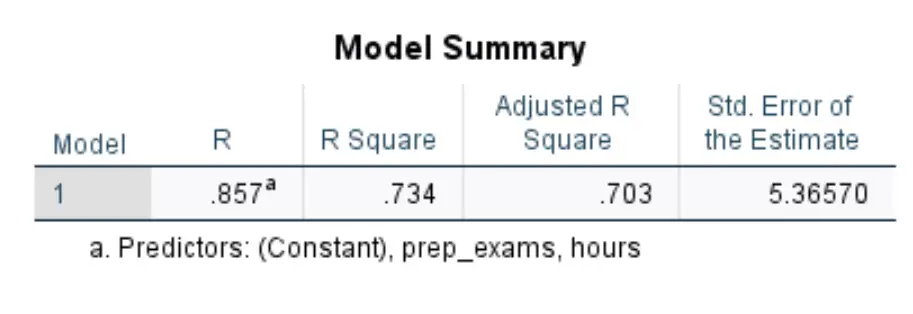
Zo interpreteert u de meest relevante cijfers in deze tabel:

• R-kwadraat: Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabelen. In dit voorbeeld kan 73,4% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren en het aantal afgelegde voorbereidende examens.
• Standaard. Schattingsfout: de standaardfout is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. In dit voorbeeld wijken de waargenomen waarden gemiddeld 5,3657 eenheden af van de regressielijn.

De volgende tabel die ons interesseert heet ANOVA :

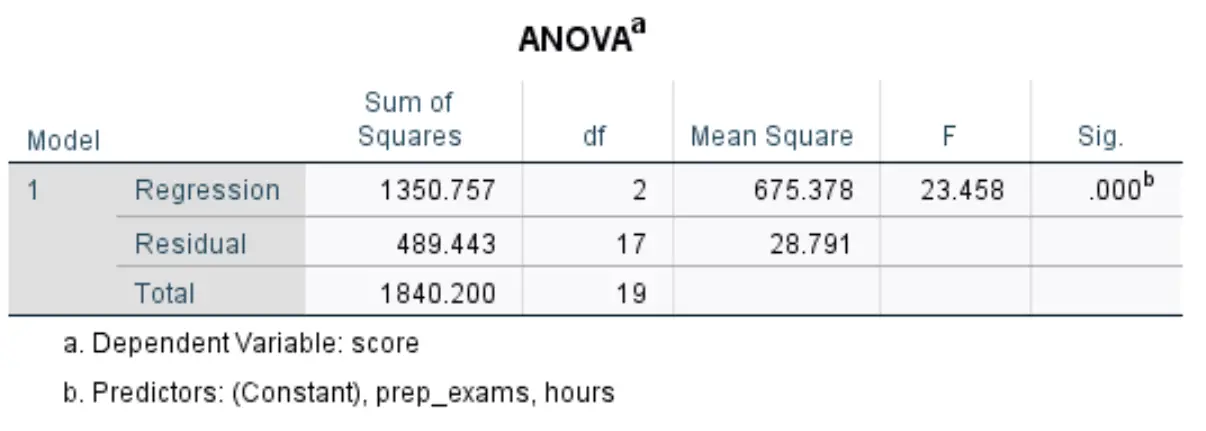
Zo interpreteert u de meest relevante cijfers in deze tabel:

• F: Dit is de algemene F-statistiek voor het regressiemodel, berekend als Mean Square Regression / Mean Square Residual.
• Sig: Dit is de p-waarde die is gekoppeld aan de algehele F-statistiek. Dit vertelt ons of het regressiemodel als geheel statistisch significant is of niet. Met andere woorden, het vertelt ons of de twee verklarende variabelen samen een statistisch significant verband hebben met de responsvariabele. In dit geval is de p-waarde gelijk aan 0,000, wat aangeeft dat de verklarende variabelen, de gestudeerde uren en de afgelegde voorbereidende examens een statistisch significant verband hebben met het examenresultaat.

De volgende tabel die ons interesseert, heeft de titel Coëfficiënten :

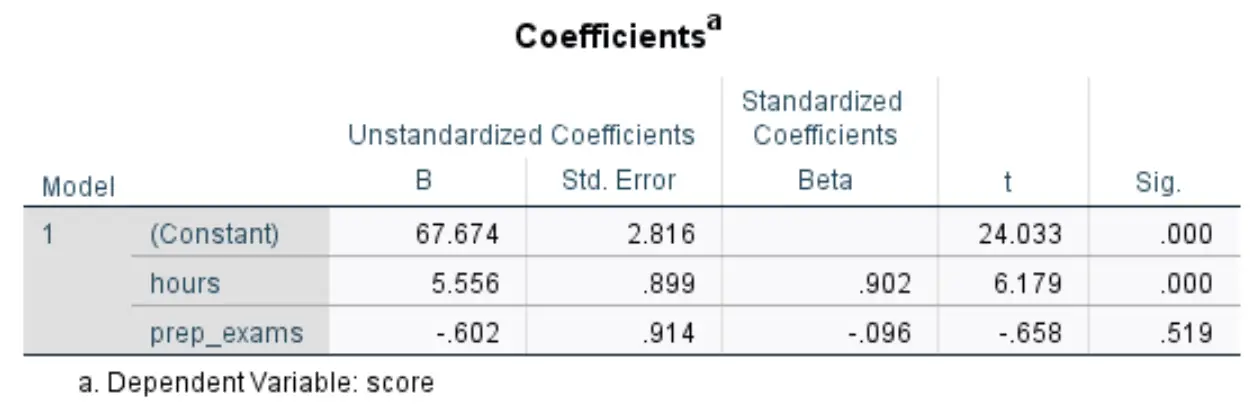
Zo interpreteert u de meest relevante cijfers in deze tabel:

• B ongestandaardiseerd (constant): dit vertelt ons de gemiddelde waarde van de responsvariabele wanneer beide voorspellende variabelen nul zijn. In dit voorbeeld is de gemiddelde examenscore 67.674 wanneer de gestudeerde uren en de afgelegde voorbereidende examens beide nul zijn.
• Niet-gestandaardiseerde B (uren): Dit vertelt ons de gemiddelde verandering in examenscores die gepaard gaat met een toename van één eenheid in studie-uren, ervan uitgaande dat het aantal afgelegde voorbereidende examens constant blijft. In dit geval gaat elk extra uur dat aan studeren wordt besteed gepaard met een stijging van de examenscore met 5.556 punten, ervan uitgaande dat het aantal afgelegde oefenexamens constant blijft.
• Niet-gestandaardiseerde B (prep_exams): Dit vertelt ons de gemiddelde verandering in de examenscore die gepaard gaat met een toename van één eenheid in het aantal afgelegde voorbereidende examens, ervan uitgaande dat het aantal bestudeerde uren constant blijft. In dit geval gaat elk bijkomend afgelegd voorbereidend examen gepaard met een daling van de examenscore met 0,602 punten, ervan uitgaande dat het aantal gestudeerde uren constant blijft.
• Zig. (uren): Dit is de p-waarde voor de verklarende variabele uren . Omdat deze waarde (0,000) kleiner is dan 0,05, kunnen we concluderen dat de bestudeerde uren een statistisch significant verband hebben met examenscores.
• Zig. (prep_exams): Dit is de p-waarde voor de verklarende variabele prep_exams . Omdat deze waarde (0,519) niet kleiner is dan 0,05 kunnen we niet concluderen dat het aantal afgelegde voorbereidende examens een statistisch significant verband heeft met het examenresultaat.

Ten slotte kunnen we een regressievergelijking vormen met behulp van de waarden die in de tabel worden weergegeven voor constant , hours en prep_exams . In dit geval zou de vergelijking zijn:

Geschatte examenscore = 67,674 + 5,556*(uren) – 0,602*(prep_exams)

We kunnen deze vergelijking gebruiken om de geschatte examenscore van een student te vinden, op basis van het aantal uren studie en het aantal oefenexamens dat hij/zij heeft afgelegd. Een student die bijvoorbeeld 3 uur studeert en 2 voorbereidende examens aflegt, zou een examenscore van 83,1 moeten krijgen:

Geschatte examenscore = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Opmerking: Omdat de verklarende variabele voor voorbereidende examens niet statistisch significant bleek te zijn, kunnen we besluiten deze uit het model te verwijderen en in plaats daarvan een eenvoudige lineaire regressie uit te voeren met bestudeerde uren als de enige verklarende variabele.