Hoe u een roc-curve in spss kunt maken en interpreteren

Logistische regressie is een statistische methode die we gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is. Om te evalueren hoe goed een logistisch regressiemodel bij een dataset past, kunnen we naar de volgende twee statistieken kijken:

• Gevoeligheid: waarschijnlijkheid dat het model een positief resultaat voorspelt voor een waarneming terwijl het resultaat daadwerkelijk positief is.
• Specificiteit: de kans dat het model een negatief resultaat voorspelt voor een waarneming terwijl het resultaat feitelijk negatief is.

Een eenvoudige manier om deze twee statistieken te visualiseren is door een ROC-curve te maken, een grafiek die de gevoeligheid en specificiteit van een logistisch regressiemodel weergeeft.

In deze tutorial wordt uitgelegd hoe u een ROC-curve in SPSS maakt en interpreteert.

Voorbeeld: ROC-curve in SPSS

Laten we zeggen dat we de volgende dataset hebben die laat zien of een basketbalspeler wel of niet is opgeroepen voor de NBA (0 = nee, 1 = ja) en zijn gemiddelde punten per wedstrijd op de universiteit:

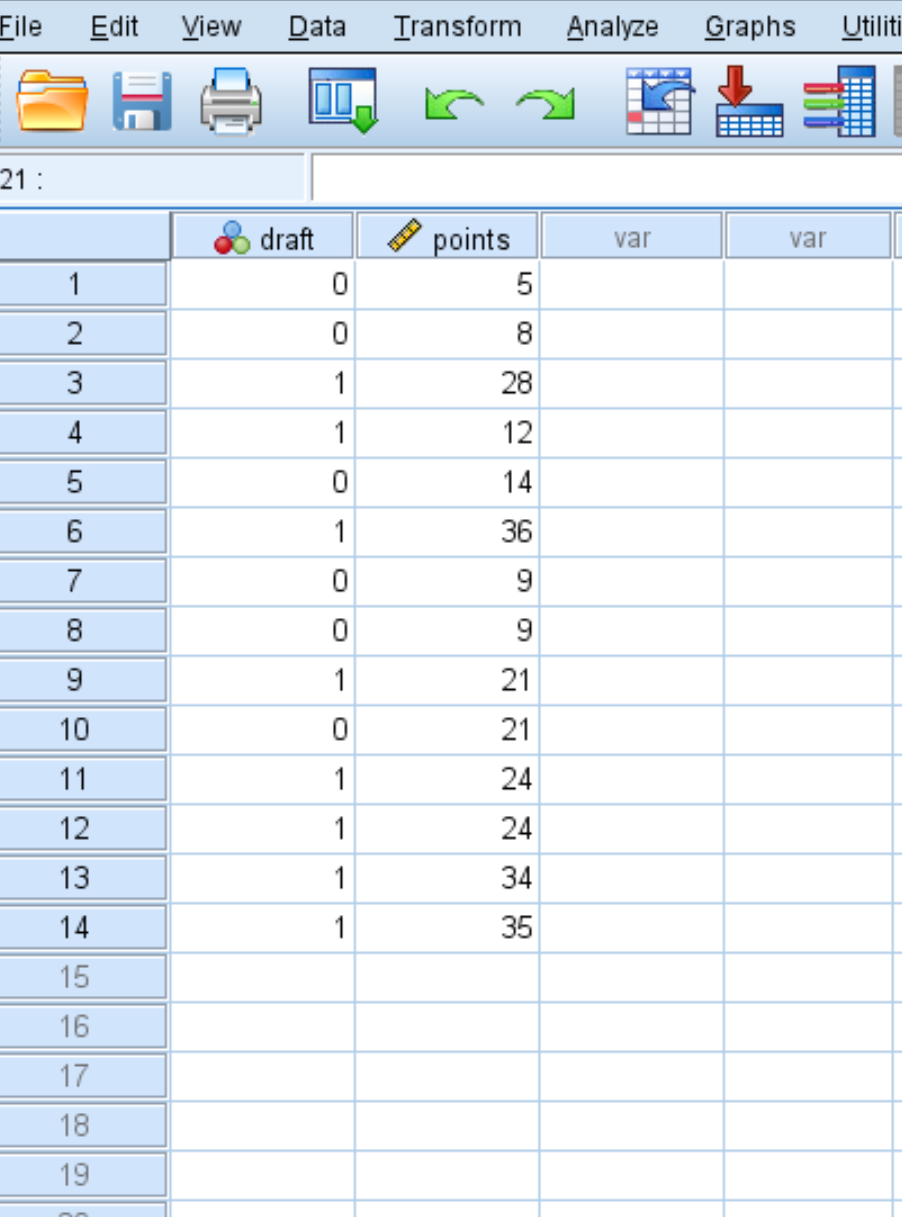
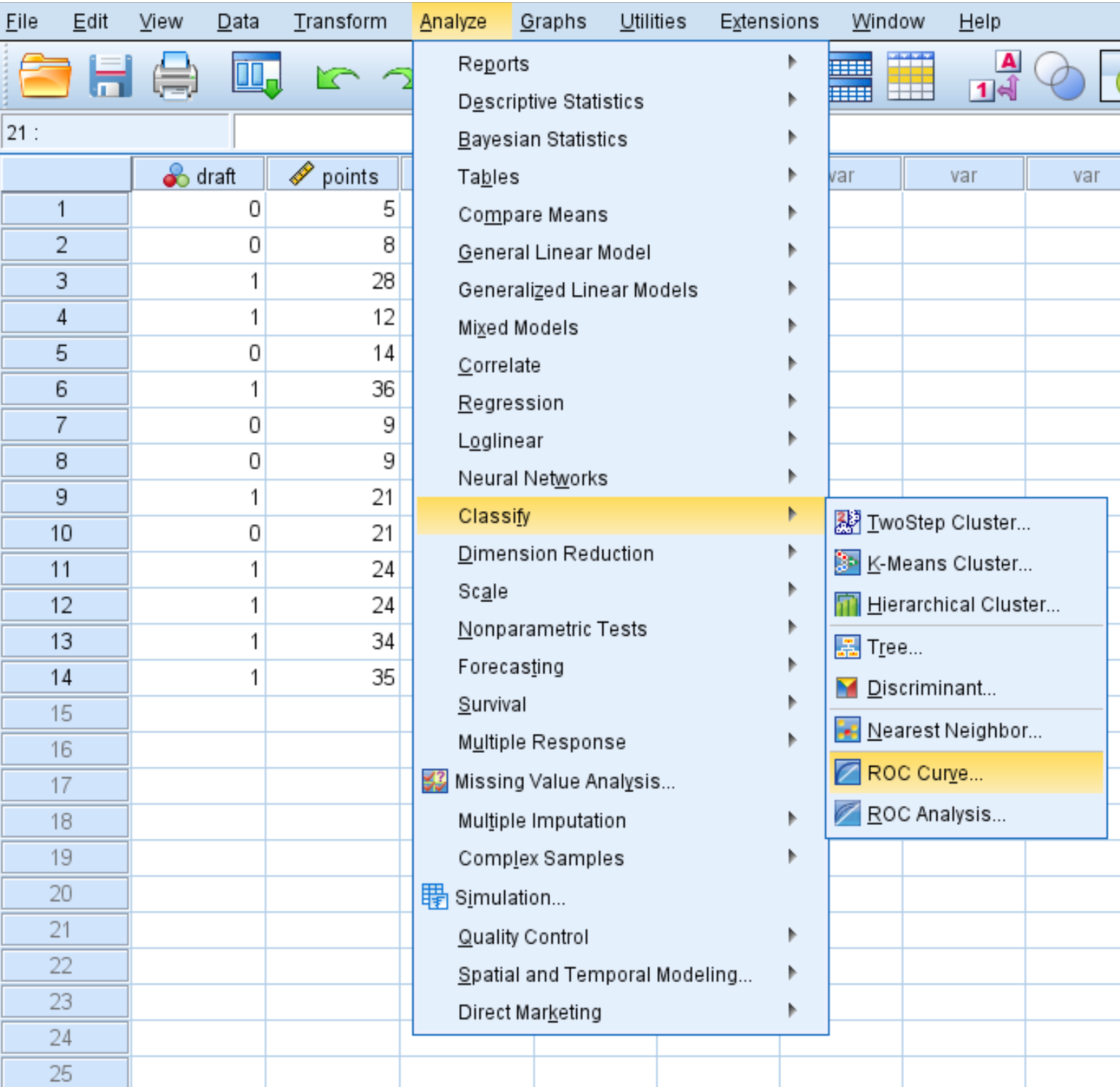
Om een ROC-curve voor deze gegevensset te maken, klikt u op het tabblad Analyseren , vervolgens op Classificeren en vervolgens op ROC-curve :

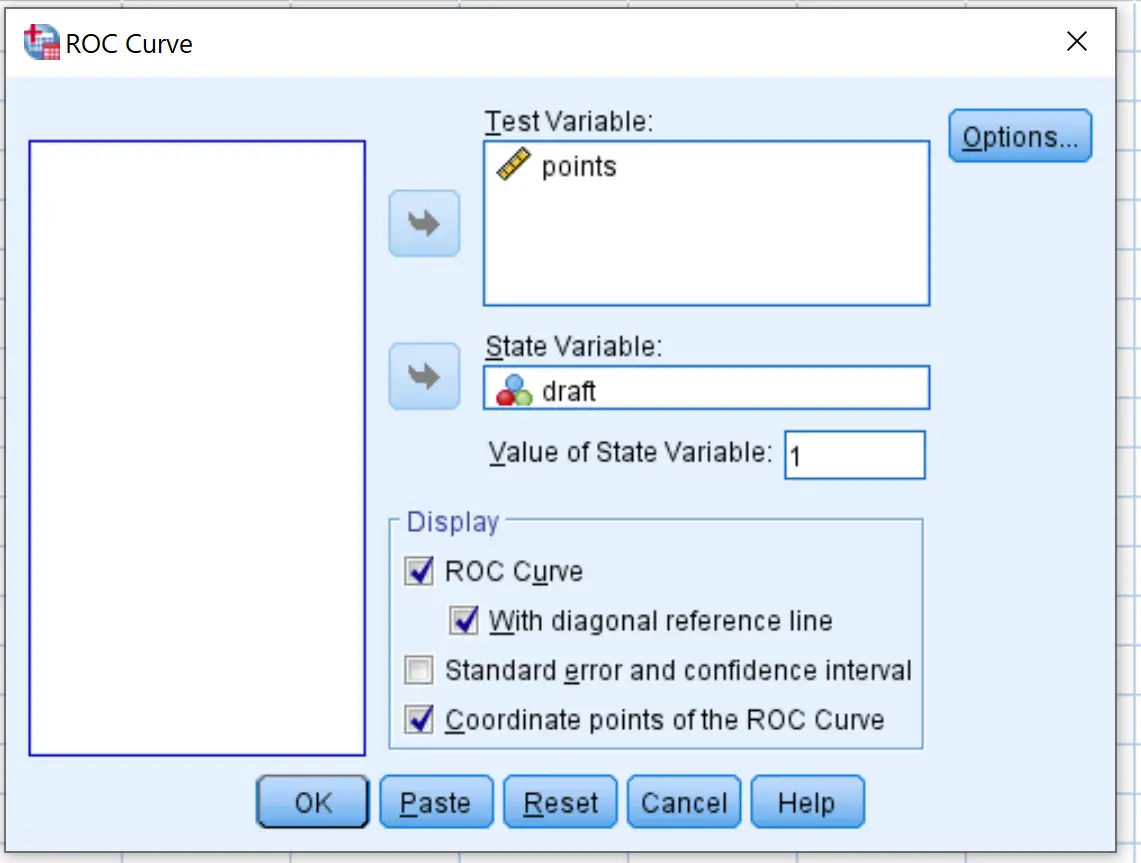
In het nieuwe venster dat verschijnt, sleept u de conceptvariabele naar het gebied met de naam Staatsvariabele. Stel de waarde van de statusvariabele in op 1 . (Dit is de waarde die aangeeft dat een speler is opgeroepen). Sleep de variabele punten naar het gebied met de naam Testvariabele.

Vink de vakjes aan naast Met diagonale referentielijn en ROC-curvepuntcoördinaten . Klik vervolgens op OK .

Zo interpreteert u het resultaat:

Samenvatting van bestandsverwerking:

Deze tabel toont het totale aantal positieve en negatieve gevallen in de dataset. In dit voorbeeld zijn 8 spelers opgeroepen (positief resultaat) en 6 spelers niet opgesteld (negatief resultaat):

ROC-curve:

De Receiver Operating Characteristic (ROC)-curve is een grafiek van gevoeligheidswaarden versus specificiteit 1 terwijl de drempelwaarde verandert van 0 naar 1:

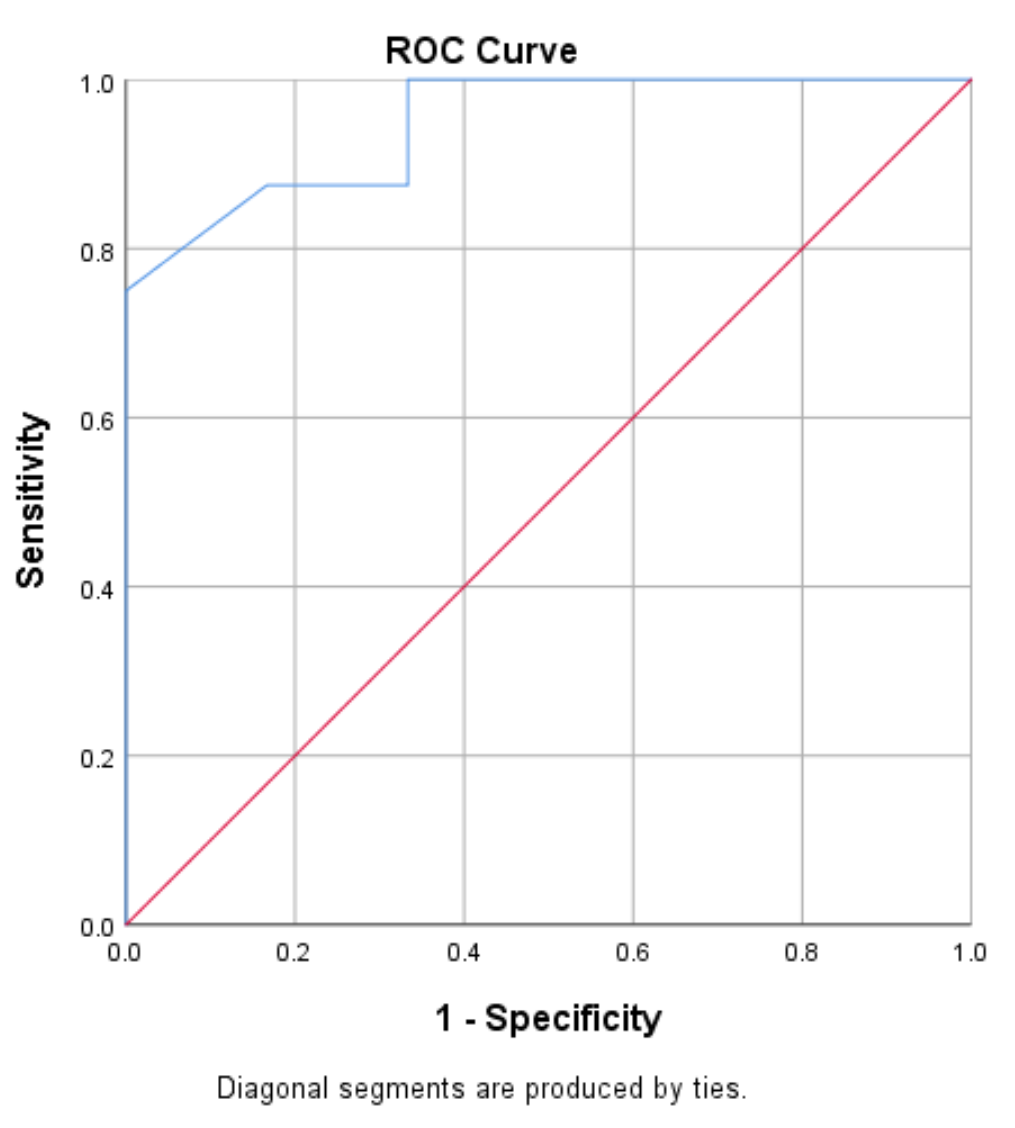
Een model met hoge gevoeligheid en specificiteit heeft een ROC-curve die in de linkerbovenhoek van de grafiek past. Een model met een lage gevoeligheid en lage specificiteit zal een curve hebben die dichtbij de diagonaal van 45 graden ligt.

We kunnen zien dat de ROC-curve (de blauwe lijn) in dit voorbeeld de linkerbovenhoek van de plot omhelst, wat aangeeft dat het model goed presteert in het voorspellen van spelers of ze wel of niet zullen worden opgeroepen, op basis van hun gemiddelde punten per spel. . .

Oppervlakte onder de curve:

Het gebied onder de curve geeft ons een idee van het vermogen van het model om onderscheid te maken tussen positieve en negatieve uitkomsten. De AUC kan variëren van 0 tot 1. Hoe hoger de AUC, hoe beter het model de resultaten correct classificeert.

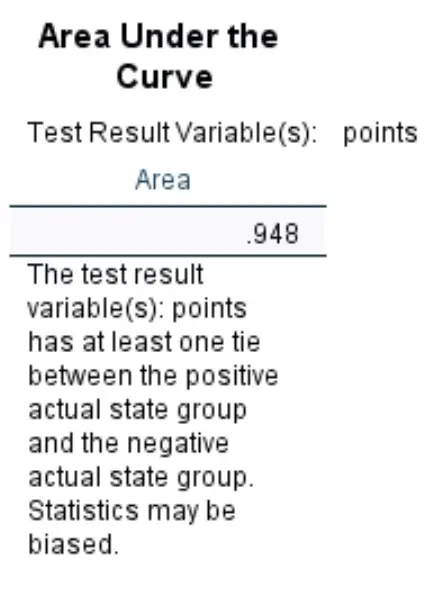
We kunnen zien dat de AUC voor dit specifieke logistische regressiemodel 0,948 is, wat extreem hoog is. Dit geeft aan dat het model goed kan voorspellen of een speler wordt opgeroepen of niet.

Coördinaten van de curve:

Deze laatste tabel toont de gevoeligheid en specificiteit 1 van de ROC-curve voor verschillende drempels.

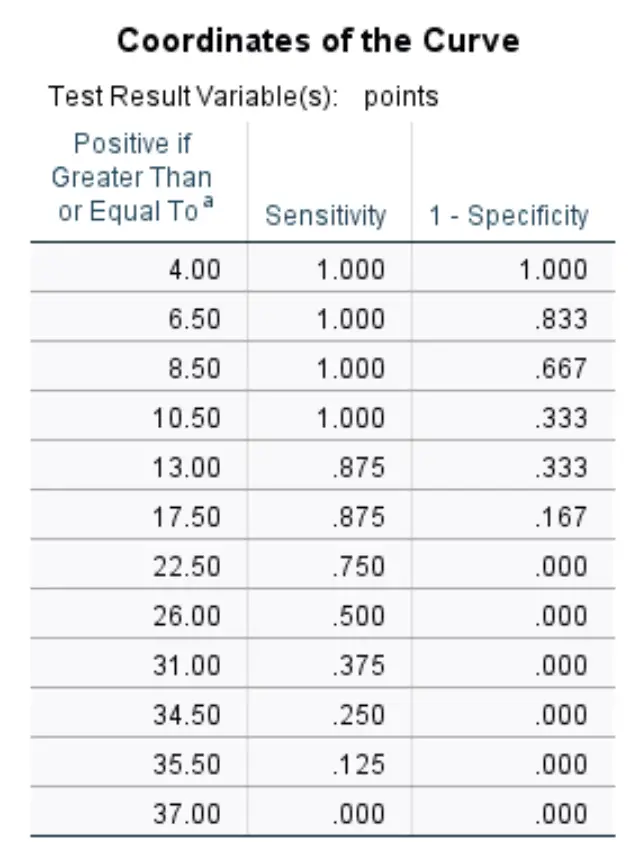
Bijvoorbeeld:

Als we toestaan dat de drempel 8,50 is, betekent dit dat we verwachten dat elke speler die minder dan 8,50 punten per spel scoort, niet wordt opgeroepen, en dat elke speler die meer dan 8,50 punten per spel scoort, wordt opgesteld.

Als we dit als drempel gebruiken, zou onze gevoeligheid 100% zijn (aangezien elke speler die minder dan 8,50 punten per spel scoorde inderdaad niet werd opgesteld) en onze specificiteit 1 66,7% zijn (aangezien 8 van de 12 spelers die meer dan 8,50 punten scoorden). per spel werden opgesteld).

In de bovenstaande tabel kunnen we de gevoeligheid en specificiteit 1 voor elke potentiële drempel zien.