Een vriendelijke gids voor de som van de kwadraten: sst, ssr, sse
Lineaire regressie wordt gebruikt om een lijn te vinden die het beste ‘past’ bij een reeks gegevens.
We gebruiken vaak drie verschillende kwadratensommen om te meten hoe goed de regressielijn daadwerkelijk bij de gegevens past:
1. Som van totale kwadraten (SST) – De som van de kwadraten van de verschillen tussen individuele gegevenspunten (y i ) en het gemiddelde van de responsvariabele ( y ).
- SST = Σ(y i – y ) 2
2. Som van kwadratenregressie (SSR) – De som van de kwadraten van de verschillen tussen de voorspelde gegevenspunten (ŷ i ) en het gemiddelde van de responsvariabele ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Som van kwadratenfout (SSE) – De som van de kwadraten van de verschillen tussen de voorspelde datapunten (ŷ i ) en de waargenomen datapunten (y i ).
- SSE = Σ(ŷ ik – y ik ) 2
Tussen deze drie maatregelen bestaat de volgende relatie:
SST = SSR + SSE
Dus als we twee van deze metingen kennen, kunnen we eenvoudige algebra gebruiken om de derde te berekenen.
SSR, SST en R-vierkant
R-kwadraat , ook wel de determinatiecoëfficiënt genoemd, is een maatstaf voor hoe goed een lineair regressiemodel bij een dataset past. Het vertegenwoordigt het deel van de variantie in deresponsvariabele dat kan worden verklaard door de voorspellende variabele.
De R-kwadraatwaarde kan variëren van 0 tot 1. Een waarde van 0 geeft aan dat de responsvariabele helemaal niet kan worden verklaard door de voorspellende variabele. Een waarde van 1 geeft aan dat de responsvariabele perfect en zonder fouten kan worden verklaard door de voorspellende variabele.
Met behulp van SSR en SST kunnen we de R-kwadraat als volgt berekenen:
R kwadraat = SSR / SST
Als de SSR voor een bepaald regressiemodel bijvoorbeeld 137,5 is en de SST 156, berekenen we de R-kwadraat als volgt:
R kwadraat = 137,5 / 156 = 0,8814
Dit vertelt ons dat 88,14% van de variatie in de responsvariabele kan worden verklaard door de voorspellende variabele.
Bereken SST, SSR, SSE: stap voor stap voorbeeld
Stel dat we de volgende dataset hebben die het aantal uren toont dat zes verschillende studenten hebben gestudeerd, samen met hun eindexamenscores:
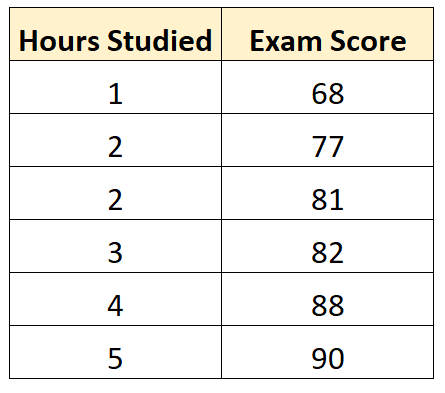
Met behulp van wat statistische software (zoals R , Excel , Python ) of zelfs met de hand kunnen we zien dat de best passende lijn is:
Score = 66.615 + 5.0769*(uren)
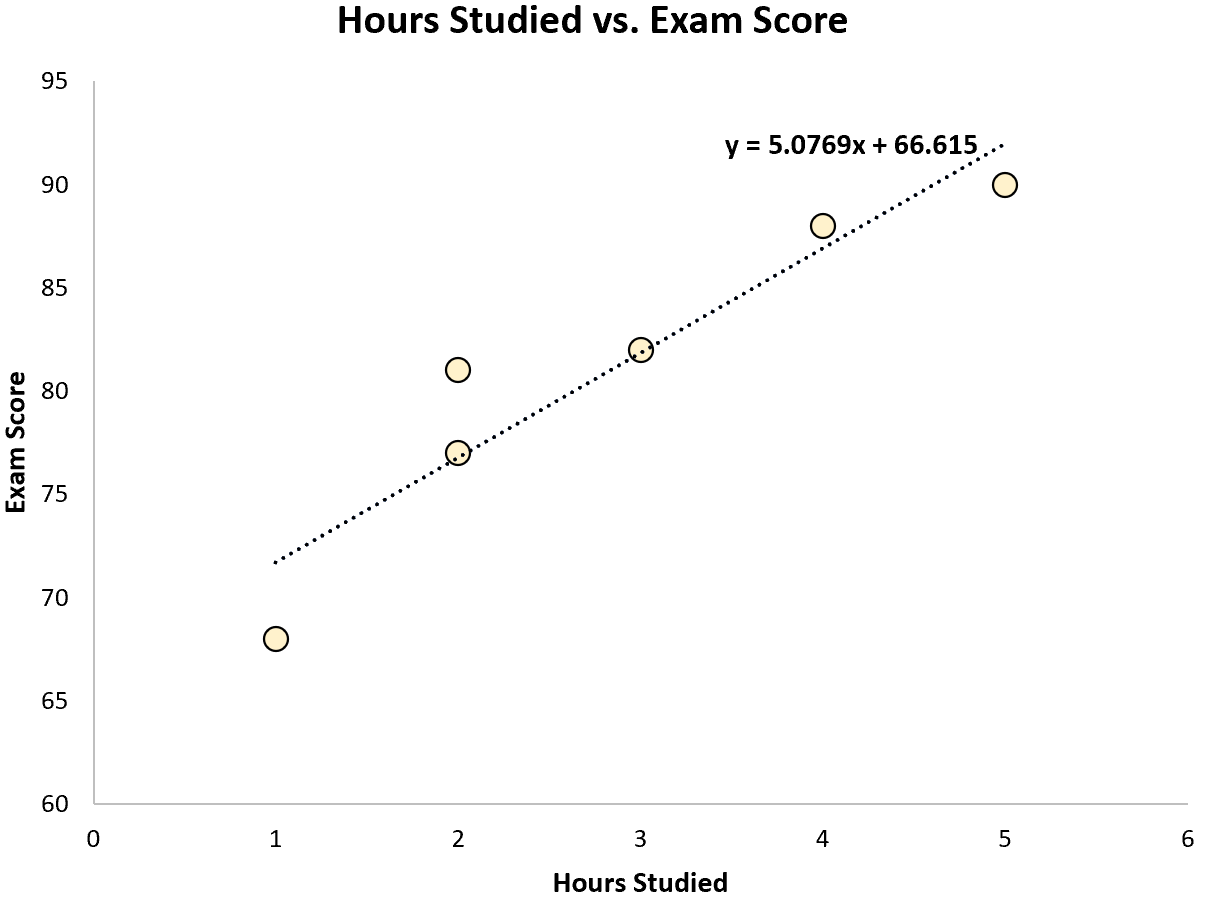
Zodra we de lijn van de best passende vergelijking kennen, kunnen we de volgende stappen gebruiken om SST, SSR en SSE te berekenen:
Stap 1: Bereken het gemiddelde van de responsvariabele.
Het gemiddelde van de responsvariabele ( y ) blijkt 81 te zijn.
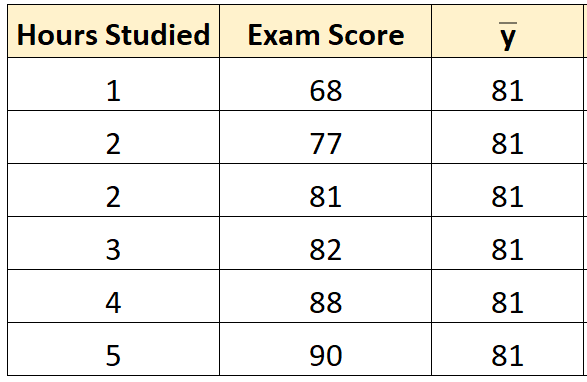
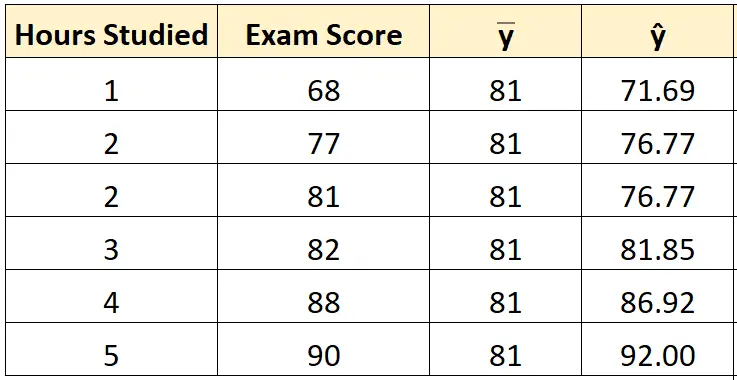
Stap 2: Bereken de voorspelde waarde voor elke waarneming.
Vervolgens kunnen we de lijn van de best passende vergelijking gebruiken om de voorspelde examenscore () voor elke student te berekenen.
Het voorspelde examencijfer voor de student die één uur heeft gestudeerd is bijvoorbeeld:
Score = 66,615 + 5,0769*(1) = 71,69 .
We kunnen dezelfde aanpak gebruiken om de voorspelde score voor elke leerling te vinden:
Stap 3: Bereken de totale som van de kwadraten (SST).
Dan kunnen we de som van de kwadraten in totaal berekenen.
De totale som van de kwadraten voor de eerste leerling is bijvoorbeeld:
(y ik – y ) 2 = (68 – 81) 2 = 169 .
We kunnen dezelfde aanpak gebruiken om de totale som van de kwadraten voor elke leerling te vinden:
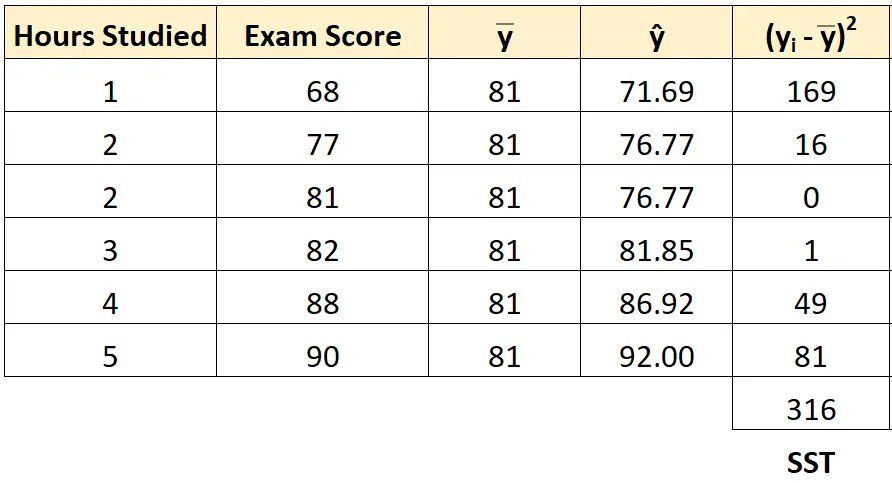
De totale som van de kwadraten blijkt 316 te zijn.
Stap 4: Bereken de som van de kwadratenregressie (SSR).
Vervolgens kunnen we de som van de kwadratenregressie berekenen.
De som van de kwadratenregressie voor de eerste leerling is bijvoorbeeld:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
We kunnen dezelfde aanpak gebruiken om de regressie van de som van de kwadraten voor elke leerling te vinden:
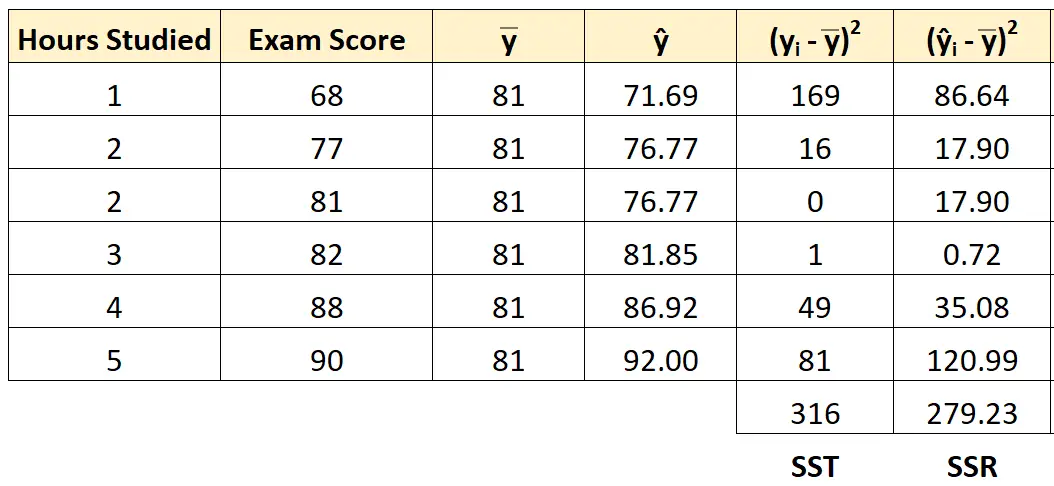
De som van de kwadratenregressie blijkt 279,23 te zijn.
Stap 5: Bereken de som van de kwadratenfout (SSE).
Dan kunnen we de fout van de som van de kwadraten berekenen.
De som van de kwadratenfout voor de eerste leerling is bijvoorbeeld:
(ŷ ik – y ik ) 2 = (71,69 – 68) 2 = 13,63 .
We kunnen dezelfde aanpak gebruiken om de som van de kwadratenfout voor elke leerling te vinden:
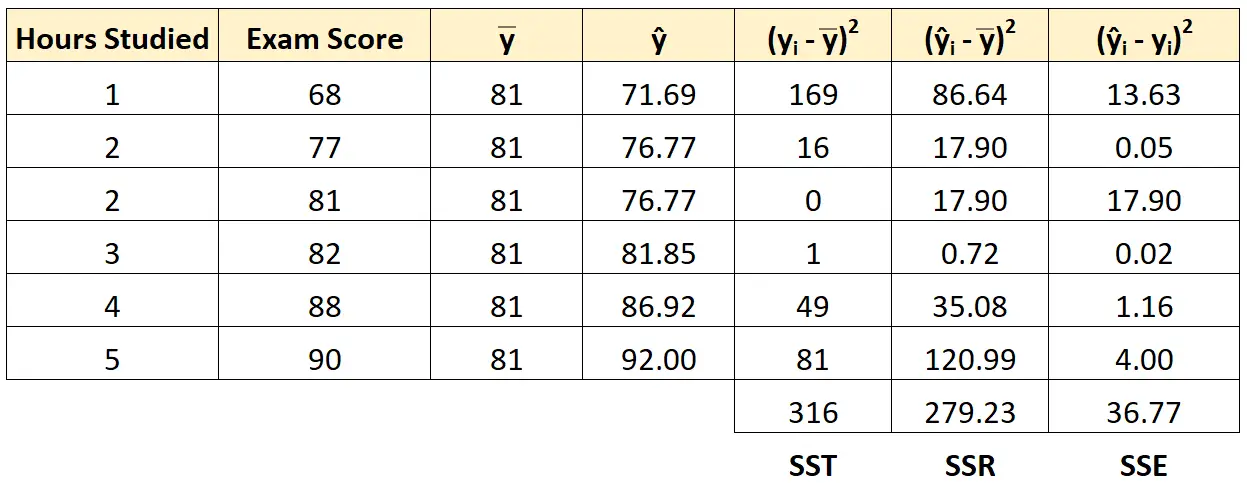
We kunnen verifiëren dat SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
We kunnen ook het R-kwadraat van het regressiemodel berekenen met behulp van de volgende vergelijking:
- R kwadraat = SSR / SST
- R kwadraat = 279,23 / 316
- R kwadraat = 0,8836
Dit leert ons dat 88,36% van de variatie in examenscores kan worden verklaard door het aantal gestudeerde uren.
Aanvullende bronnen
U kunt de volgende rekenmachines gebruiken om SST, SSR en SSE automatisch te berekenen voor elke eenvoudige lineaire regressielijn:
SST-calculator
RSS-calculator
ESS-calculator
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder