Hoe sst, ssr en sse in excel te berekenen

We gebruiken vaak drie verschillende kwadratensommen om te meten hoe goed een regressielijn daadwerkelijk bij een dataset past:

1. Som van totale kwadraten (SST) – De som van de kwadraten van de verschillen tussen individuele gegevenspunten (y _i ) en het gemiddelde van de responsvariabele ( y ).

• SST = Σ(y _i – y ) ²

2. Som van kwadratenregressie (SSR) – De som van de kwadraten van de verschillen tussen de voorspelde gegevenspunten (ŷ _i ) en het gemiddelde van de responsvariabele ( y ).

• SSR = Σ(ŷ _i – y ) ²

3. Som van kwadratenfout (SSE) – De som van de kwadraten van de verschillen tussen de voorspelde datapunten (ŷ _i ) en de waargenomen datapunten (y _i ).

• SSE = Σ(ŷ _ik – y _ik ) ²

In het volgende stapsgewijze voorbeeld ziet u hoe u elk van deze metrieken voor een bepaald regressiemodel in Excel kunt berekenen.

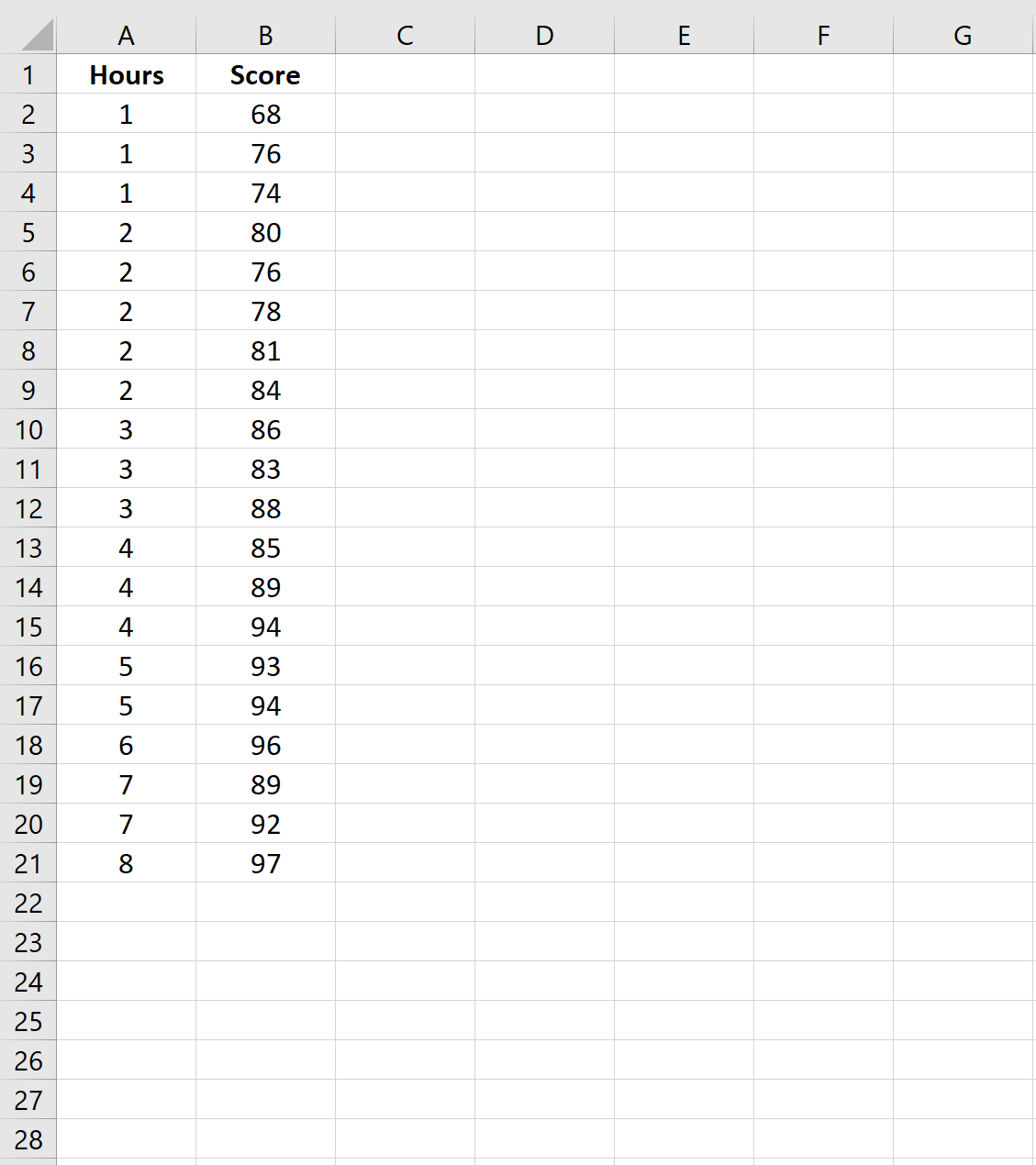
Stap 1: Creëer de gegevens

Laten we eerst een dataset maken met het aantal gestudeerde uren en de behaalde examenscores voor 20 verschillende leerlingen op een bepaalde school:

Stap 2: Pas een regressiemodel toe

Klik op het bovenste lint van Excel op het tabblad Gegevens en klik op Gegevensanalyse . Als u deze optie niet ziet, moet u eerst de gratis Analysis ToolPak-software installeren .

Zodra u op Data-analyse klikt, verschijnt een nieuw venster. Selecteer Regressie en klik op OK.

Geef in het nieuwe venster dat verschijnt de volgende informatie op:

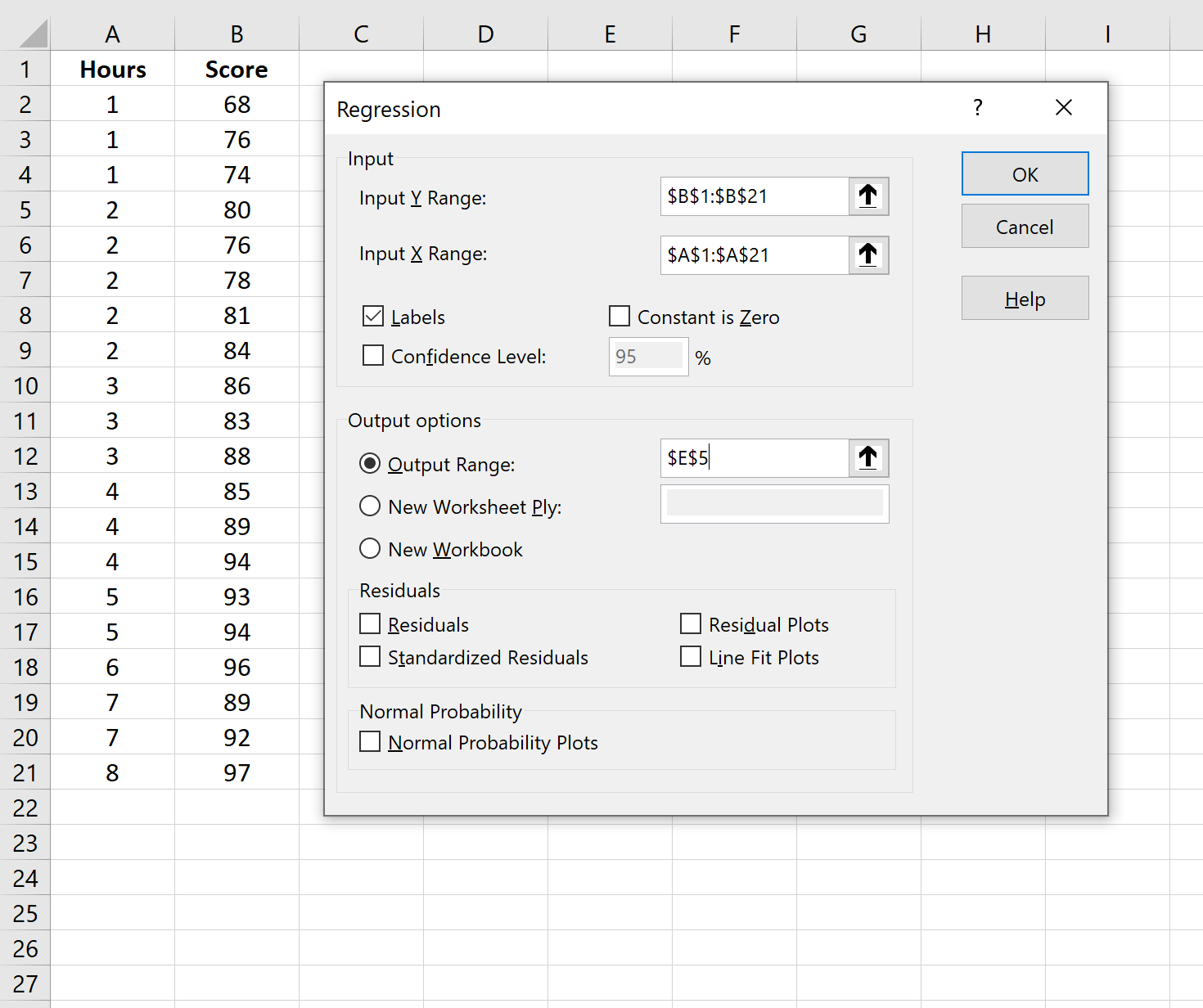
Zodra u op OK klikt, verschijnt de regressie-uitvoer.

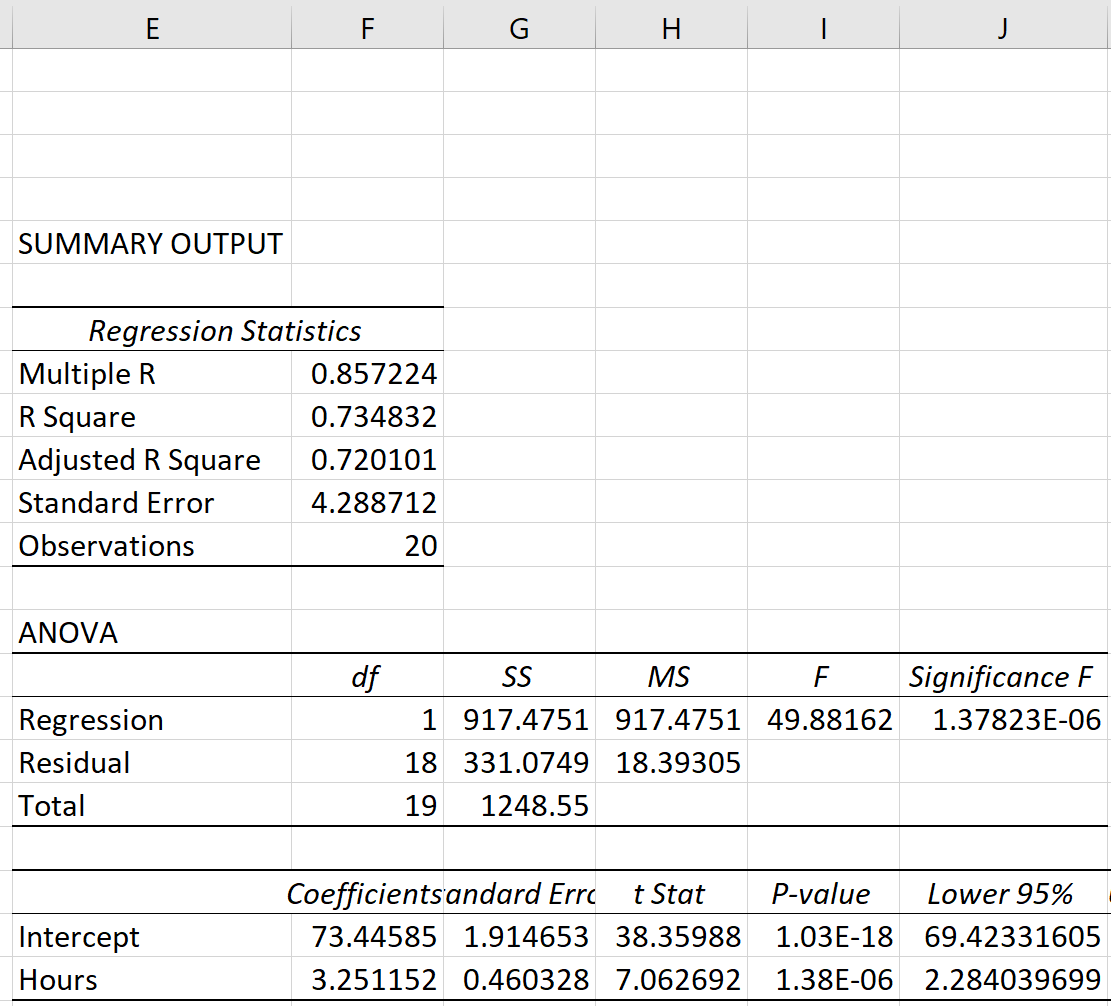
Stap 3: Analyseer het resultaat

De drie kwadratensomstatistieken – SST, SSR en SSE – zijn te zien in de SS- kolom van de ANOVA- tabel:

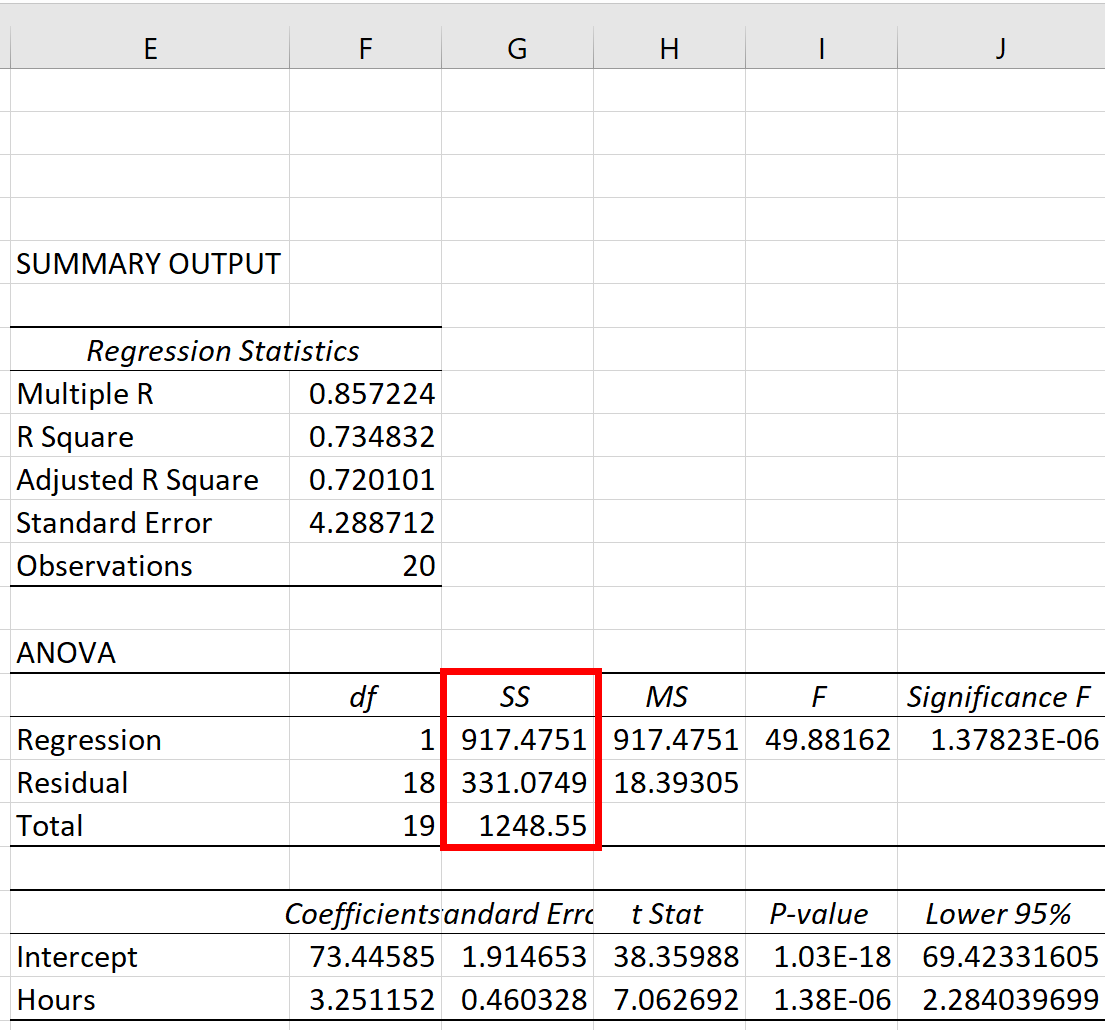
De statistieken blijken te zijn:

• Totale som van kwadraten (SST): 1248,55
• Som van kwadratenregressie (SSR): 917,4751
• Som van kwadratenfout (SSE): 331,0749

We kunnen verifiëren dat SST = SSR + SSE:

• SST = SSR + SSE
• 1248,55 = 917,4751 + 331,0749

We kunnen ook handmatig het R-kwadraat van het regressiemodel berekenen:

• R kwadraat = SSR / SST
• R kwadraat = 917,4751 / 1248,55
• R kwadraat = 0,7348

Dit vertelt ons dat 73,48% van de variatie in examenscores kan worden verklaard door het aantal gestudeerde uren.

Aanvullende bronnen

Hoe u eenvoudige lineaire regressie uitvoert in Excel
Hoe u meerdere lineaire regressies uitvoert in Excel
Hoe polynomiale regressie uit te voeren in Excel
Exponentiële regressie uitvoeren in Excel