Stam- en bladdiagram

In dit artikel wordt uitgelegd wat stam- en bladdiagrammen in de statistiek zijn en waarvoor ze worden gebruikt. Je ontdekt dus hoe je een stam-bladdiagram construeert, opgeloste oefeningen voor dit soort statistische grafieken en, ten slotte, wat de voor- en nadelen zijn van het stam-bladdiagram.

Wat is het stam-bladdiagram?

Stam- en bladdiagram is een soort statistisch diagram waarin een reeks kwantitatieve gegevens wordt weergegeven.

In een stam-bladdiagram wordt elk gegevenspunt gescheiden door het blad , wat het laatste cijfer is, en de stam , wat de overige cijfers zijn. In een stam-bladdiagram wordt dus elk blad op de lijn van de bijbehorende stengel geplaatst.

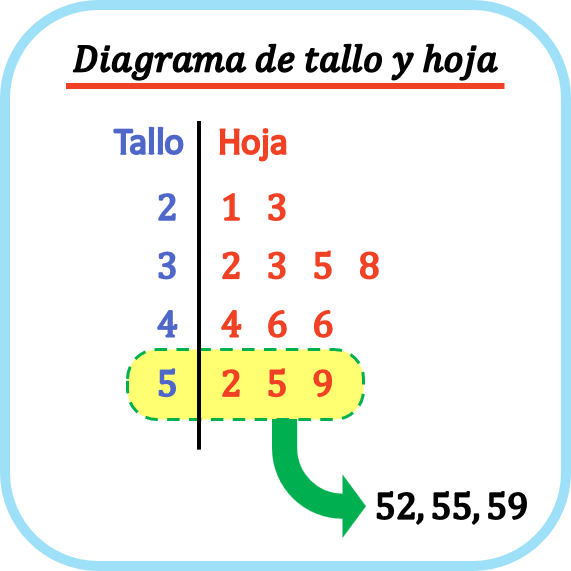
Op deze manier helpen stengel- en bladplots om een reeks statistische gegevens grafisch weer te geven en ook om de vorm van de verdeling te visualiseren.

Stam- en bladdiagram wordt ook wel stengel- en bladdiagram genoemd, een naam die uit het Engels komt.

Het plotten van stengels en bladeren lijkt sterk op het histogram , hoewel dit andere type statistische grafiek wordt gebruikt voor grotere steekproeven.

Hoe u een stam- en bladdiagram maakt

Volg deze stappen om een stengel- en bladdiagram te maken :

1. Sorteer de gegevens van klein naar groot.
2. Rond indien nodig de cijfers af tot ze het gewenste aantal cijfers hebben.
3. Bepaal in welke figuur de snede wordt gemaakt tussen de stengel en het blad, dat wil zeggen, bepaal het aantal cijfers dat de bladeren zullen hebben. Normaal gesproken is het blad zo ontworpen dat het alleen het laatste cijfer van elk gegevensitem bevat.
4. Vertegenwoordig elk stukje gegevens in het stengel- en bladdiagram. De stengels worden in oplopende volgorde in de linkerkolom geplaatst, terwijl de bladeren in de rechterkolom worden geplaatst ter hoogte van de bijbehorende stengel en ook in oplopende volgorde.

Voorbeeld van een stam- en bladplot

Om u te laten zien hoe u een stam- en bladdiagram maakt, lossen we hieronder twee voorbeelden op: één zonder decimalen en de andere met decimalen.

voorbeeld 1

• Teken de volgende gegevensreeksen in een stengel- en bladdiagram:

In dit geval zijn de gegevens al geordend en afgerond, dus het is niet nodig om deze twee stappen uit te voeren. Omdat getallen dus twee cijfers hebben, worden ze zo weergegeven dat de tijden de stam vormen en de tijden de bladeren van de grafiek.

We zullen eerst de stam van het diagram weergeven. De tijd van de gegevens loopt op tot 9, dus we maken een regel voor elke tien:

En dan vertegenwoordigen we de bladeren, hiervoor plaatsen we de eenheid van elke gegevens in de overeenkomstige regel. Het getal 57 gaat bijvoorbeeld naar de wortel 5 en in de rechterkolom voegen we een 7 toe.

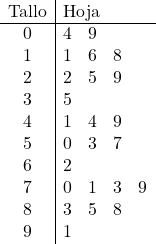
En op deze manier werden alle monstergegevens weergegeven in een stengel- en bladplot.

Voorbeeld 2

• Vergelijk de volgende twee gegevensvoorbeelden met decimalen met behulp van een stengel-en-bladplot.

Zoals je in deze oefening zult zien, kan een enkele stam-en-bladgrafiek worden gebruikt om twee statistische steekproeven weer te geven. Daarom zullen we beide sets gegevens in hetzelfde stengel-en-bladdiagram plotten: één aan de linkerkant en één aan de rechterkant. Dit type plot wordt een dubbelstammig stam-en-bladplot genoemd.

In dit geval nemen we het hele deel van de getallen als stam van het diagram en aan de andere kant zijn de decimalen de bladeren van het diagram. We construeren daarom de stengel- en bladindeling door alle hele onderdelen te plaatsen:

En nu plaatsen we het blad van elke gegevens in de stam die ermee overeenkomt:

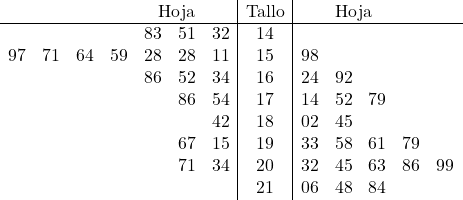
Door de gegevens grafisch weer te geven, kunnen we deze eenvoudig vergelijken. Concreet zien we dat de voorbeeldgegevens aan de rechterkant iets groter zijn dan de steekproef aan de linkerkant, en daarom zal het gemiddelde ook groter zijn. Afhankelijk van het doel van het statistische onderzoek zullen we dus geïnteresseerd zijn in het kiezen van deze of gene steekproef.

Houd er rekening mee dat u niet alleen moet weten hoe u een slash- en blade-diagram moet maken, maar dat u ook moet weten hoe u het diagram moet interpreteren.

Voor- en nadelen van stam- en bladplot

Vanwege de kenmerken van het stengel- en bladplot hebben dit soort percelen de volgende voor- en nadelen:

Voordeel:

• Door de stengels en bladeren te volgen, kunt u de vorm van een verdeling zien.
• Er kunnen twee verdelingen worden vergeleken met behulp van de dubbelstammige stam-en-bladgrafiek.
• Hiermee kunt u snel uitschieters in een dataset identificeren.
• U kunt de modus van de gegevensreeksen met het oog bepalen.

Nadelen:

• Het stengel- en bladdiagram wordt steeds minder gebruikt omdat computersoftware snel een complexere grafiek kan maken.
• De te representeren steekproefomvang is beperkt, doorgaans tussen 15 en 150 datapunten.
• Alleen kwantitatieve gegevens kunnen worden weergegeven.