Standaardafwijking in google spreadsheets (steekproef en populatie)

Standaarddeviatie is een van de meest gebruikelijke manieren om de verdeling van waarden in een dataset te meten.

Er zijn twee verschillende soorten standaarddeviaties die u kunt berekenen, afhankelijk van het type gegevens waarmee u werkt.

1. Standaardafwijking van de populatie

U moet de standaarddeviatie van de populatie berekenen wanneer de dataset waarmee u werkt een gehele populatie vertegenwoordigt, dat wil zeggen elke waarde waarin u geïnteresseerd bent.

De formule voor het berekenen van een populatiestandaarddeviatie, aangeduid met σ, is:

σ = √ Σ(x _ik – μ) ² / N

Goud:

• Σ : Een symbool dat “som” betekent
• x _i : De i- ^de waarde in een gegevensset
• μ : Het populatiegemiddelde
• N : Populatieomvang

2. Voorbeeld van standaardafwijking

U moet de standaarddeviatie van de steekproef berekenen als de gegevensset waarmee u werkt een steekproef vertegenwoordigt die is genomen uit een grotere populatie waarin u geïnteresseerd bent.

De formule voor het berekenen van een steekproefstandaarddeviatie, aangeduid als s , is:

s = √ Σ(x _ik – x̄) ² / (n – 1)

Goud:

• Σ : Een symbool dat “som” betekent
• x _i : De i- ^de waarde in een gegevensset
• x̄ : De steekproefgemiddelden
• n : De steekproefomvang

De volgende voorbeelden laten zien hoe u de standaardafwijking van de steekproef en de populatie in Google Spreadsheets kunt berekenen.

Voorbeeld 1: Berekening van een standaarddeviatie van een steekproef in Google Spreadsheets

Stel dat een bioloog de standaarddeviatie van het gewicht van een bepaalde schildpadsoort wil samenvatten, en dus een eenvoudige willekeurige steekproef van twintig schildpadden uit de populatie neemt.

Omdat het een steekproef gebruikt om de standaarddeviatie van de populatie te schatten, kan het de standaarddeviatie van de steekproef berekenen.

De volgende schermafbeelding laat zien hoe u de functie STDEV.S() gebruikt om de standaarddeviatie van het monster te berekenen:

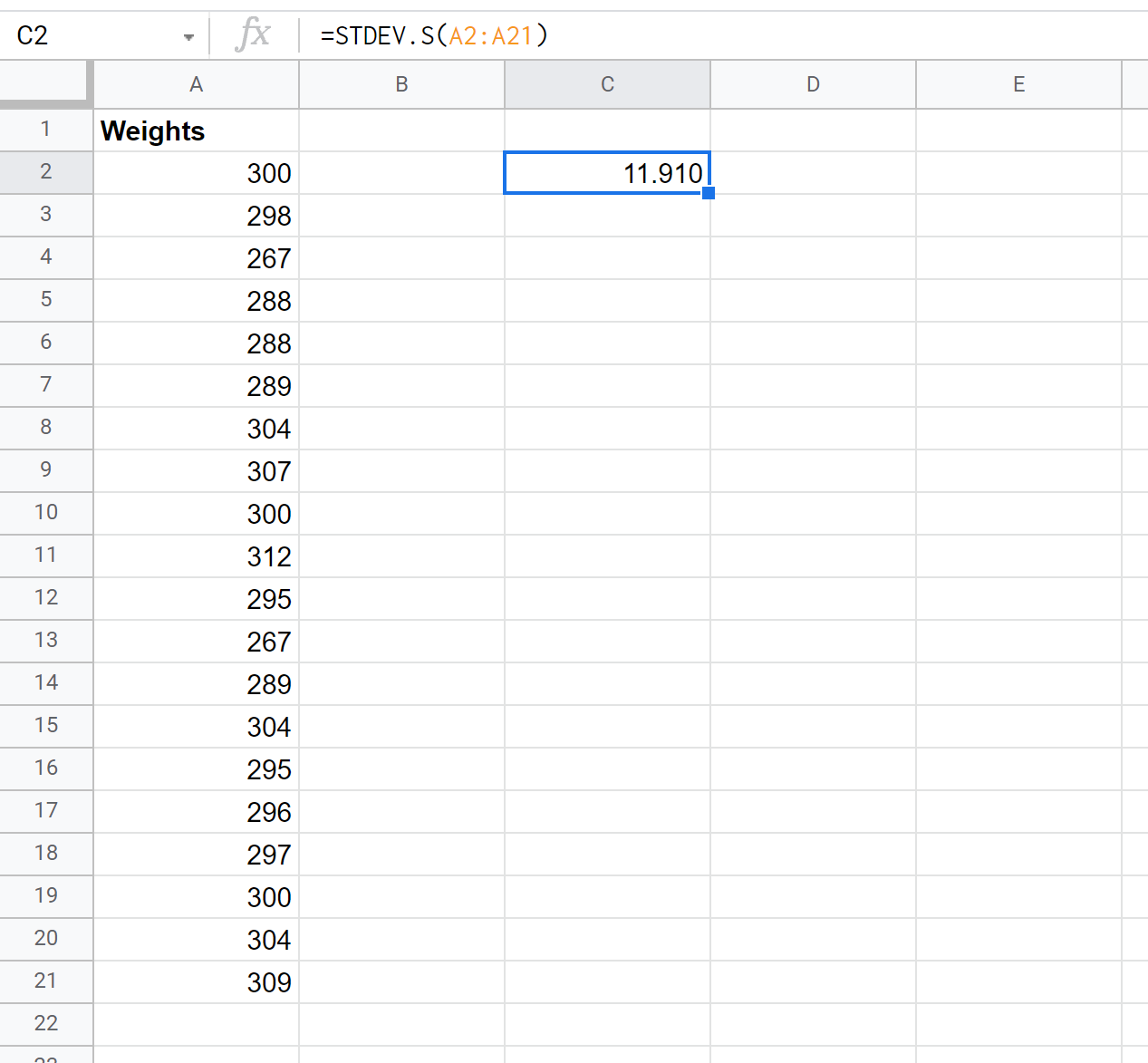
De standaarddeviatie van de steekproef blijkt 11,91 te zijn.

Houd er rekening mee dat STDEV() ook de standaarddeviatie van het monster retourneert.

Voorbeeld 2: Berekening van de standaarddeviatie van de populatie in Google Spreadsheets

Stel dat een basketbalcoach de standaarddeviatie wil samenvatten van de punten die door de twaalf spelers van zijn team zijn gescoord.

Omdat hij alleen geïnteresseerd is in de punten die zijn spelers scoren en niet in andere spelers van een ander team, kan hij de standaarddeviatie van de populatie berekenen.

De volgende schermafbeelding laat zien hoe u de functie STDEV.P() gebruikt om de standaarddeviatie van de populatie te berekenen:

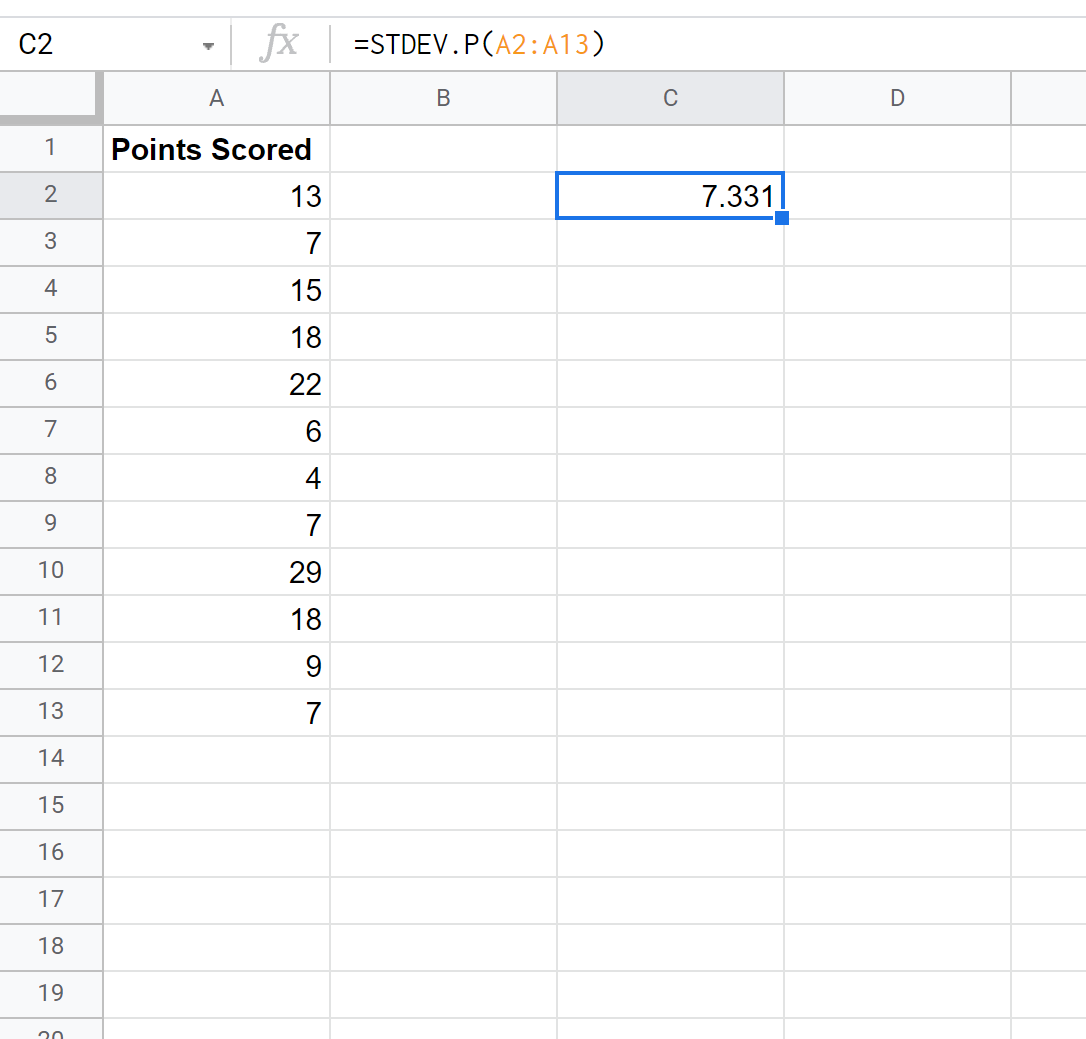
De standaarddeviatie van de populatie blijkt 7.331 te zijn.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de standaarddeviatie:

• Bevolking versus Voorbeeldstandaardafwijking: wanneer moet u deze gebruiken?
• Variatiecoëfficiënt versus standaardafwijking: het verschil
• Waarom is standaarddeviatie belangrijk?

In de volgende tutorials wordt uitgelegd hoe u andere spreidingsstatistieken in Google Spreadsheets kunt berekenen:

• Hoe het interkwartielbereik in Google Spreadsheets te berekenen
• Hoe de variatiecoëfficiënt in Google Spreadsheets te berekenen