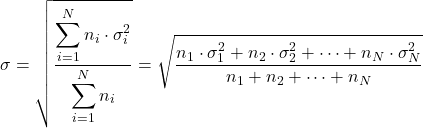Standaardafwijking (of standaardafwijking)

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat standaarddeviatie, ook wel standaarddeviatie genoemd, is. Je leert hoe je de standaarddeviatie berekent, een stapsgewijs praktijkvoorbeeld en een online calculator om de standaarddeviatie van elk gegevensmonster te vinden.

Wat is de standaardafwijking (of standaardafwijking)?

Standaardafwijking , ook wel standaardafwijking genoemd, is een maatstaf voor statistische spreiding. Met andere woorden, de standaarddeviatie is een waarde die de spreiding van een reeks statistische gegevens aangeeft.

Daarom wordt de standaardafwijking (of standaardafwijking) gebruikt om de spreiding van een populatie of statistische steekproef te kwantificeren. Hoe groter de standaarddeviatie van een gegevensreeks, hoe meer verspreid de gegevens zijn. En de interpretatie kan ook in de andere richting plaatsvinden: als de standaarddeviatie laag is, betekent dit dat de gegevens over het algemeen zeer dicht bij het gemiddelde liggen.

Bij het berekenen van de standaard- of typische deviatie over een populatie is het symbool voor standaarddeviatie de Griekse letter sigma (σ). Maar als het gaat om de standaarddeviatie van de steekproef, wordt de letter s gebruikt om de statistische meting weer te geven.

In sommige statistieken en waarschijnlijkheidsboeken wordt de standaardafwijking ook wel de standaardafwijking genoemd.

Formule voor standaardafwijking (of standaardafwijking).

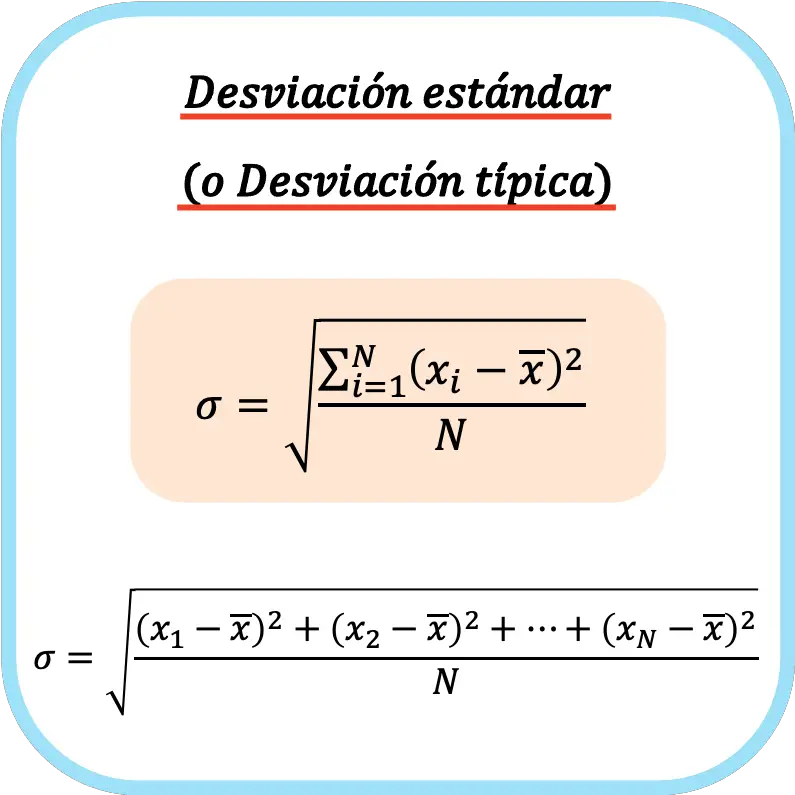
De standaarddeviatie (of standaarddeviatie) is gelijk aan de vierkantswortel van de som van de kwadraten van de afwijkingen van de gegevensreeks gedeeld door het totale aantal waarnemingen.

De formule voor het berekenen van de standaardafwijking (of standaardafwijking) is daarom:

👉 U kunt de onderstaande rekenmachine gebruiken om de standaardafwijking van elke dataset te berekenen.

Concluderend: om de standaarddeviatie van een dataset te vinden, moet u alle afwijkingen berekenen (gedefinieerd als het verschil tussen een datapunt en het rekenkundig gemiddelde), de afwijkingen verhogen tot twee, ze allemaal bij elkaar optellen en vervolgens delen door de totaal. aantal gegevens en neem ten slotte de vierkantswortel.

Voorbeeld van standaardafwijking (of standaardafwijking)

Gezien de definitie van standaardafwijking (of typische afwijking), vindt u hieronder een stapsgewijs voorbeeld, zodat u kunt zien hoe de standaardafwijking van een gegevensreeks wordt berekend.

Bereken de standaardafwijking van de volgende waarden: 3, 6, 2, 9, 4.

Het eerste wat we moeten doen is het steekproefgemiddelde bepalen. Om dit te doen, tellen we alle gegevens bij elkaar op en delen we deze door het totale aantal waarnemingen, namelijk vijf:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

We gebruiken nu de standaardafwijkingsformule:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

We vervangen de gegevens in de formule:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

En tenslotte berekenen we de standaarddeviatie:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Standaardafwijking (of standaardafwijking) Calculator

Voer een reeks statistische gegevens in de volgende online rekenmachine in om de standaardafwijking (of standaardafwijking) te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Standaard (of typische) afwijking voor gegroepeerde gegevens

Om de standaardafwijking (of standaardafwijking) van gegevens gegroepeerd in intervallen te berekenen , moeten de volgende stappen worden gevolgd:

Zoek het gemiddelde van de gegroepeerde gegevens.
Bereken afwijkingen van gegroepeerde gegevens.
Maak elke opening vierkant.
Vermenigvuldig elk vorig resultaat met de frequentie van het interval.
Voeg de som toe van alle waarden verkregen in de vorige stap.
Deel door het totale aantal waarnemingen.
Neem de vierkantswortel van de vorige waarde. Het resulterende getal is de standaardafwijking van de gegroepeerde gegevens.

Concluderend is de formule voor het berekenen van de standaardafwijking van gegevens gegroepeerd in intervallen:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

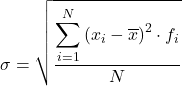
Hoewel de bovenstaande formule normaal gesproken wordt gebruikt, kan de volgende algebraïsche uitdrukking ook worden gebruikt, aangezien hetzelfde resultaat wordt verkregen:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

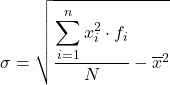
Hieronder vindt u een stapsgewijze oefening over de standaarddeviatie van gegevens gegroepeerd in intervallen, zodat u kunt zien hoe dit wordt gedaan. Preciezer gezegd, de standaardafwijking van de volgende statistische gegevens wordt berekend:

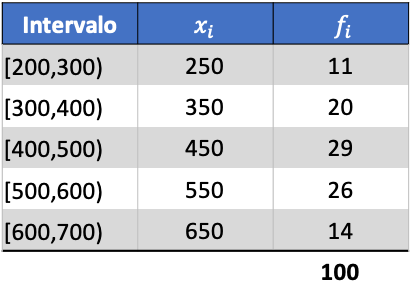
voorbeeld van gegevens gegroepeerd in intervallen

Eerst vermenigvuldigen we de klassescore van elk interval met de frequentie ervan om het rekenkundig gemiddelde te berekenen:

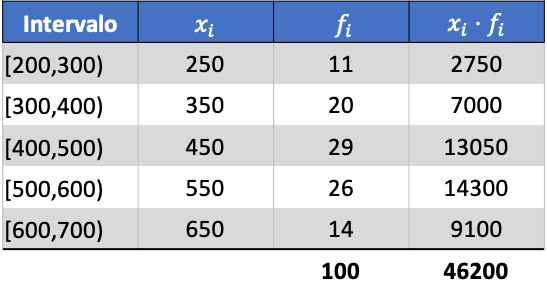
Het gemiddelde van de gegroepeerde gegevens is dus:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

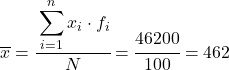
Nu we de waarde van het gemiddelde kennen, moeten we de volgende drie kolommen aan de gegevenstabel toevoegen:

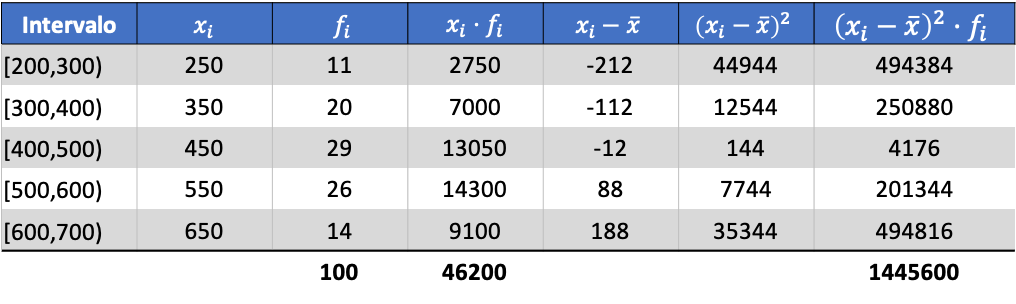
opgeloste oefening van standaardafwijking of standaardafwijking voor gegroepeerde gegevens

De standaardafwijking van de gegroepeerde gegevens is dan het resultaat van de vierkantswortel van het totaal van de laatste kolom gedeeld door het totale aantal waarnemingen:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

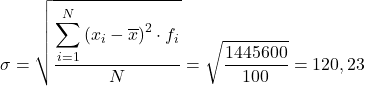
Standaard (of typische) afwijking en variantie

De relatie tussen standaardafwijking (of typische afwijking) en variantie is dat standaardafwijking de vierkantswortel van de variantie is.

Dus als we de variantiewaarde van een dataset kennen, kunnen we eenvoudig de standaarddeviatie berekenen door de vierkantswortel te nemen. Of omgekeerd, als we de standaarddeviatie kennen, kunnen we de variantie vinden door de waarde te kwadrateren.

$Var(X)=\sigma^2$

In feite kan de variantie eenvoudig worden weergegeven door het gekwadrateerde standaardafwijkingssymbool te gebruiken. Daarom is het symbool voor populatievariantie sigma-kwadraat (σ ² ) en het symbool voor steekproefvariantie s-kwadraat (s ² ).

Bovendien hebben de concepten standaarddeviatie en variantie een vergelijkbare interpretatie, aangezien beide de spreiding van een reeks statistische gegevens laten zien.

Eigenschappen van standaardafwijking (of standaardafwijking)

De standaarddeviatie heeft de volgende eigenschappen:

De standaarddeviatie van een gegevensmonster kan niet negatief zijn.

$\sigma \ge 0$

De standaardafwijking is nul als alle gegevens hetzelfde zijn.

$\sigma =0$

Als aan alle gegevens een constante term wordt toegevoegd, verandert de waarde van de standaardafwijking niet.

$\sigma (X+k)=\sigma (X)$

Als alle gegevens met een getal worden vermenigvuldigd, wordt de standaardafwijking vermenigvuldigd met de absolute waarde van dat getal.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

De standaardafwijking van de som van twee willekeurige variabelen is gelijk aan de vierkantswortel van de som van de varianties van de variabelen plus tweemaal de covariantie tussen de twee variabelen.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Als we de standaardafwijkingen van de verschillende verdelingen (σ _i ) en hun aantal gegevens (n _i ) kennen, kunnen we de totale standaardafwijking berekenen door de volgende formule toe te passen:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder