Hoe de standaarddeviatie van een kansverdeling te vinden

Een kansverdeling vertelt ons de waarschijnlijkheid dat een willekeurige variabele bepaalde waarden aanneemt.

De volgende kansverdeling vertelt ons bijvoorbeeld de waarschijnlijkheid dat een bepaald voetbalteam een bepaald aantal doelpunten zal scoren in een bepaalde wedstrijd:

Om de standaardafwijking van een kansverdeling te vinden, kunnen we de volgende formule gebruiken:

σ = √ Σ(x _ik -μ) ² * P(x _ik )

Goud:

• x _i : De ^i-de waarde
• μ: Het gemiddelde van de verdeling
• P( _xi ): De waarschijnlijkheid van de ^i- de waarde

Beschouw bijvoorbeeld onze kansverdeling voor het voetbalteam:

Het gemiddelde aantal doelpunten van het voetbalteam zou als volgt worden berekend:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 doelpunten.

We kunnen dan de standaarddeviatie als volgt berekenen:

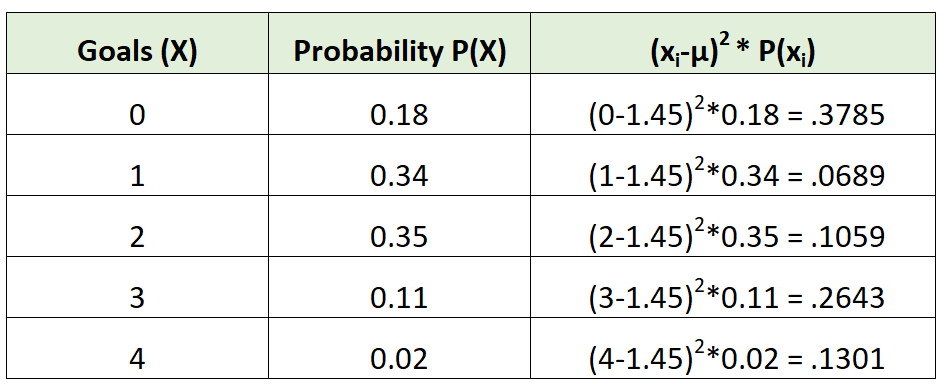
De standaardafwijking is de vierkantswortel van de som van de waarden in de derde kolom. We zouden het dus als volgt berekenen:

Standaardafwijking = √ (.3785 + .0689 + .1059 + .2643 + .1301) = 0,9734

De variantie is eenvoudigweg de standaardafwijking in het kwadraat, dus:

Afwijking = 0,9734 ² = 0,9475

De volgende voorbeelden laten zien hoe u de standaardafwijking van een kansverdeling in enkele andere scenario’s kunt berekenen.

Voorbeeld 1: Standaardafwijking van voertuigpech

De volgende kansverdeling vertelt ons de waarschijnlijkheid dat een bepaald voertuig gedurende een periode van 10 jaar een bepaald aantal batterijstoringen zal ervaren:

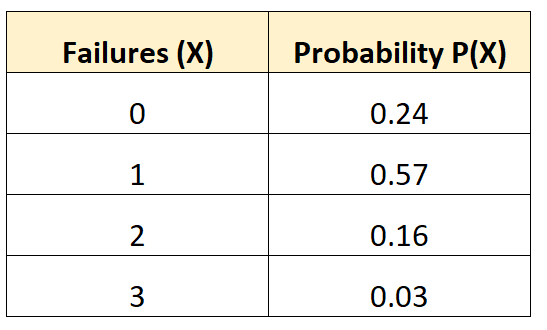
Vraag: Wat is de standaardafwijking van het aantal pechgevallen voor dit voertuig?

Oplossing: Het gemiddelde aantal verwachte storingen wordt als volgt berekend:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 storingen.

We kunnen dan de standaarddeviatie als volgt berekenen:

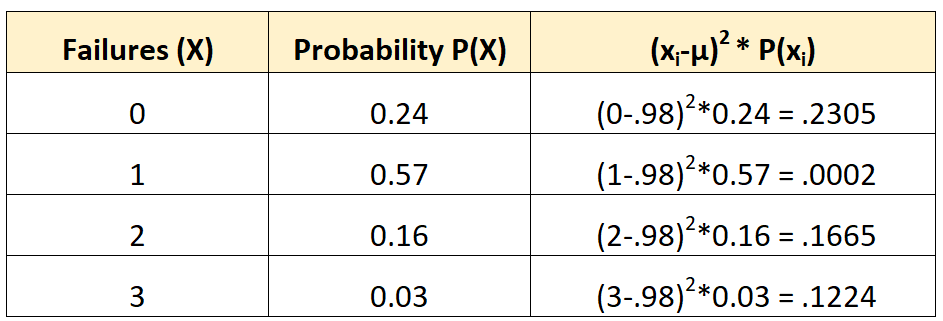
De standaardafwijking is de vierkantswortel van de som van de waarden in de derde kolom. We zouden het dus als volgt berekenen:

Standaardafwijking = √ (.2305 + .0002 + .1665 + .1224) = 0,7208

Voorbeeld 2: Standaardafwijking van de verkoop

De volgende kansverdeling vertelt ons de waarschijnlijkheid dat een bepaalde verkoper de komende maand een bepaald aantal verkopen zal realiseren:

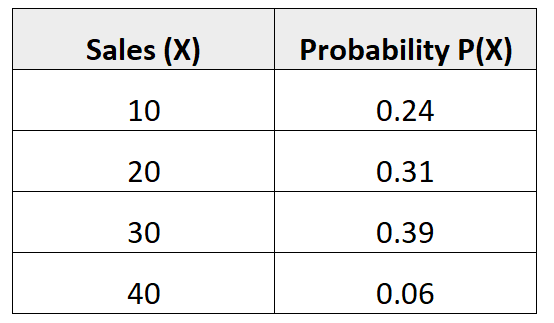
Vraag: Wat is de standaardafwijking van het aantal verkopen van deze verkoper in de komende maand?

Oplossing: Het gemiddelde aantal verwachte verkopen wordt als volgt berekend:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 vuil.

We kunnen dan de standaarddeviatie als volgt berekenen:

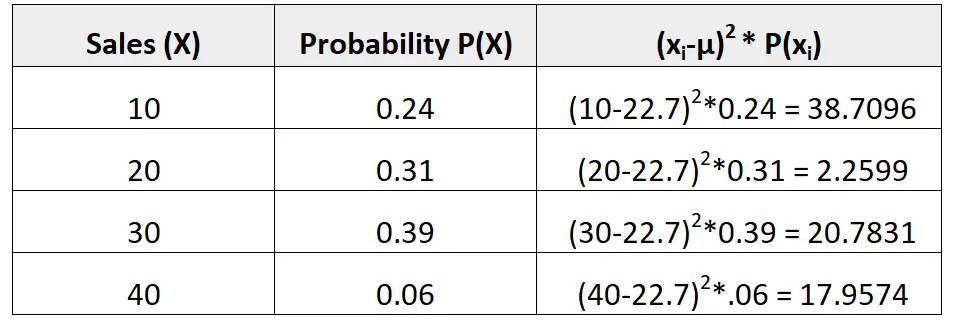
De standaardafwijking is de vierkantswortel van de som van de waarden in de derde kolom. We zouden het dus als volgt berekenen:

Standaardafwijking = √ (38,7096 + 2,2599 + 20,7831 + 17,9574) = 8,928

Aanvullende bronnen

Hoe het gemiddelde van een kansverdeling te vinden
Kansverdelingscalculator