Hoe de standaardafwijking van elk histogram te schatten

Een histogram biedt een handige manier om de verdeling van waarden in een dataset te visualiseren.

De x-as van een histogram geeft groepen gegevenswaarden weer en de y-as vertelt ons hoeveel waarnemingen in een gegevensset zich in elke groep bevinden.

Omdat een histogram waarnemingen in vakken plaatst, is het niet mogelijk om de exacte standaardafwijking te berekenen van de gegevensset die door het histogram wordt weergegeven, maar het is wel mogelijk om de standaardafwijking te schatten.

Het volgende voorbeeld laat zien hoe u dit doet.

Gerelateerd: Hoe u het gemiddelde en de mediaan van elk histogram kunt schatten

Hoe de standaardafwijking van een histogram te schatten

Om de standaarddeviatie van een histogram te schatten, moet u eerst het gemiddelde schatten.

Om het gemiddelde te schatten kunnen we de volgende formule gebruiken:

Gemiddeld: Σm _i n _i / N

Goud:

• m _i : Het midden van de i- ^de bak
• n _i : De frequentie van de i- ^de bak
• N: De totale steekproefomvang

Stel dat we bijvoorbeeld het volgende histogram hebben:

Zo schat u de gemiddelde waarde van dit histogram:

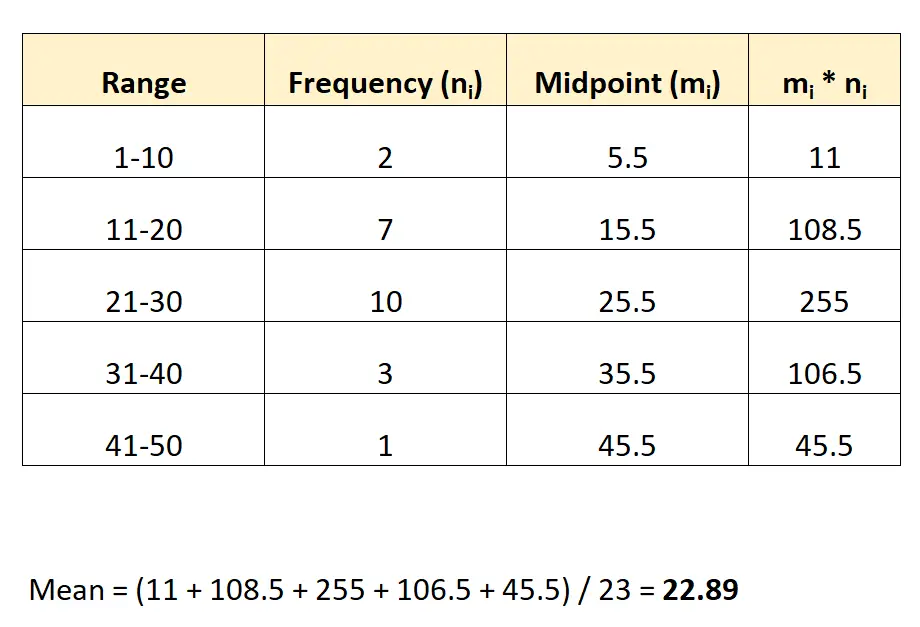
Wij schatten het gemiddelde op 22,89 .

Opmerking: het middelpunt van elke groep kan worden gevonden door het gemiddelde te nemen van de onderste en bovenste waarden van het bereik. Het middelpunt van de eerste groep wordt bijvoorbeeld als volgt berekend: (1+10) / 2 = 5,5.

Nu we een schatting van het gemiddelde hebben, kunnen we de volgende formule gebruiken om de standaardafwijking te schatten:

Standaardafwijking: √ Σn _i (m _i -μ) ² / (N-1)

Goud:

• n _i : De frequentie van de i- ^de bak
• m _i : Het midden van de i- ^de bak
• µ : Het gemiddelde
• N: De totale steekproefomvang

Zo passen we deze formule toe op onze dataset:

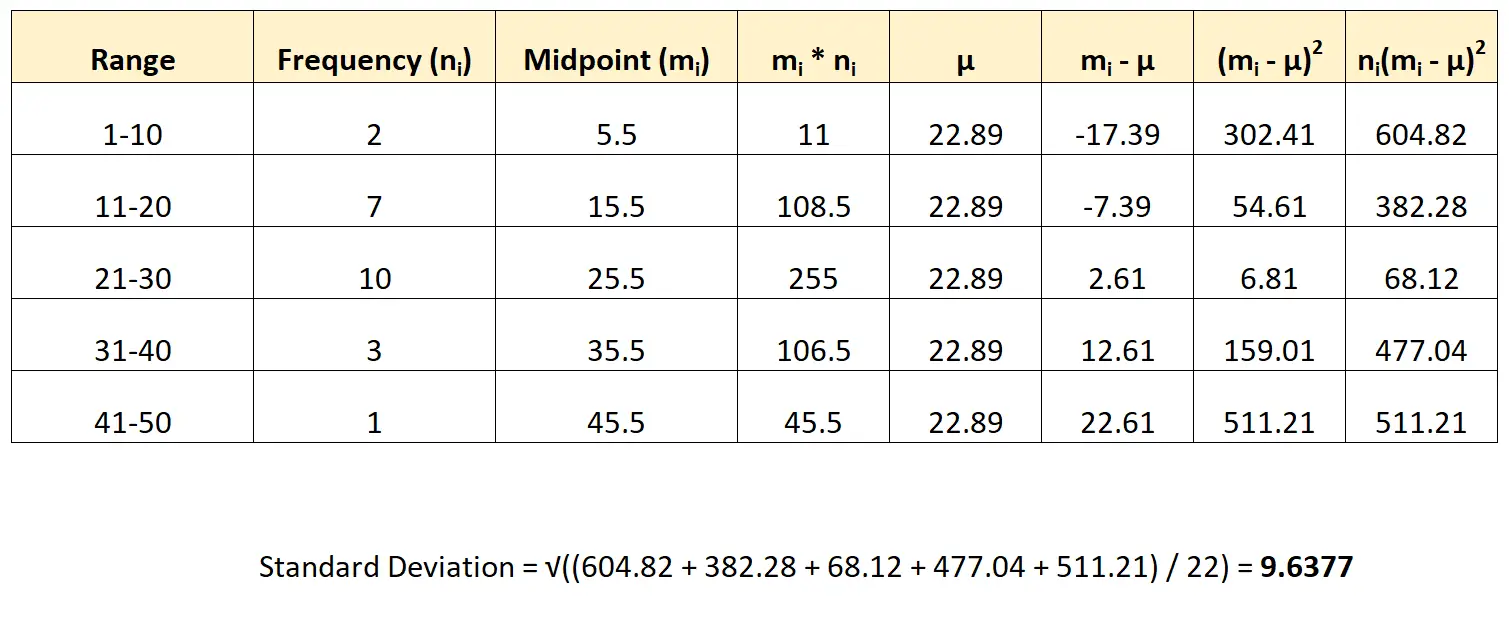We schatten de standaardafwijking van de dataset op 9,6377 .

Hoewel het niet gegarandeerd is dat het exact overeenkomt met de standaardafwijking van de dataset (aangezien we de ruwe gegevenswaarden van de dataset niet kennen), vertegenwoordigt het onze beste schatting van de standaardafwijking.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken uitvoert die verband houden met gegevens die in groepen zijn gegroepeerd:

Hoe u de variantie van gegroepeerde gegevens kunt vinden
Hoe u de mediaan van gegroepeerde gegevens kunt vinden
Hoe de gegroepeerde gegevensmodus te vinden