Standaardafwijking en standaardfout: wat is het verschil?

Twee termen die studenten vaak verwarren in de statistiek zijn standaarddeviatie en standaardfout .

Standaardafwijking meet de verdeling van waarden in een dataset.

De standaardfout is de standaardafwijking van het gemiddelde van herhaalde steekproeven uit een populatie.

Laten we eens naar een voorbeeld kijken om dit idee duidelijk te illustreren.

Voorbeeld: standaardafwijking versus standaardfout

Stel dat we het gewicht van 10 verschillende schildpadden meten.

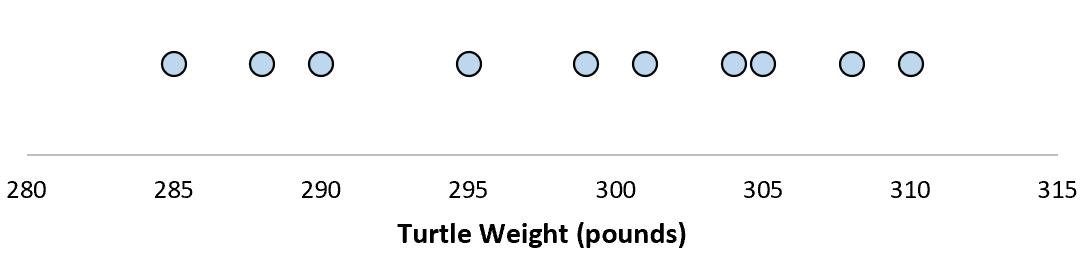
Voor deze steekproef van 10 schildpadden kunnen we het steekproefgemiddelde en de standaardafwijking van de steekproef berekenen:

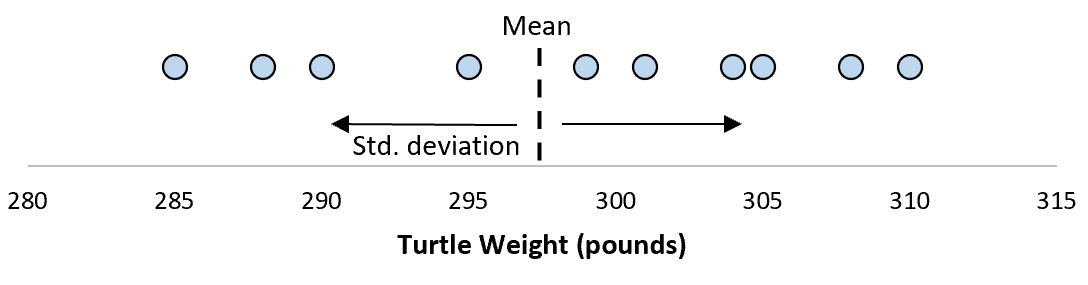
Stel dat de standaardafwijking 8,68 is. Dit geeft ons een idee van de gewichtsverdeling van deze schildpadden.

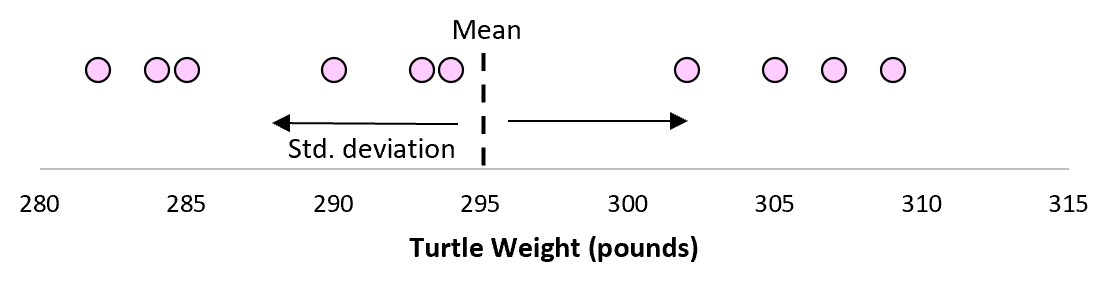
Maar stel dat we nog een eenvoudig willekeurig monster van tien schildpadden verzamelen en ook hun metingen doen.

Het is meer dan waarschijnlijk dat deze steekproef van tien schildpadden een iets ander gemiddelde en een iets andere standaarddeviatie zal hebben, ook al komen ze uit dezelfde populatie:

Als we ons nu voorstellen dat we herhaalde steekproeven uit dezelfde populatie nemen en het steekproefgemiddelde en de steekproefstandaarddeviatie voor elk monster registreren:

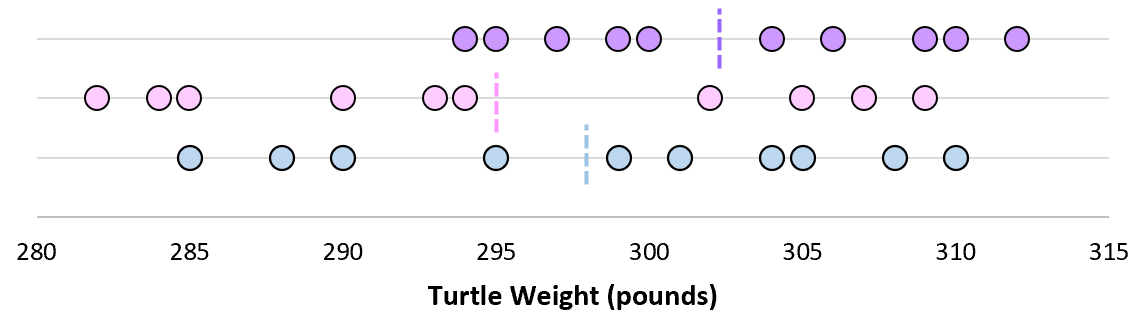
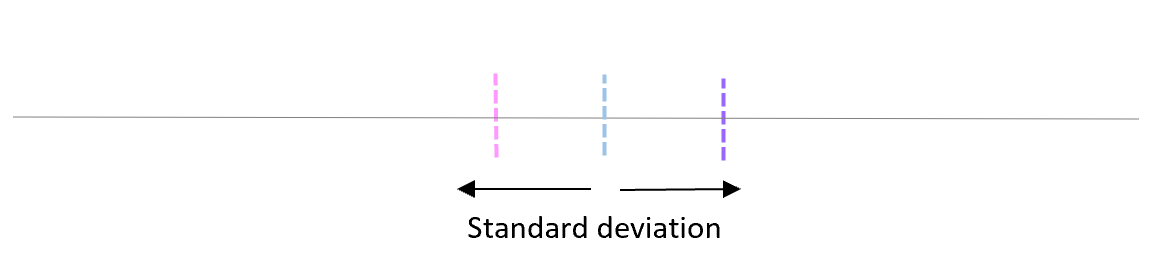
Stel je nu voor dat we elk van de steekproefgemiddelden op dezelfde lijn plotten:

De standaarddeviatie van deze gemiddelden wordt de standaardfout genoemd.

De formule om de standaardfout daadwerkelijk te berekenen is:

Standaardfout = s/ √ n

Goud:

• s: standaardafwijking van het monster
• n: steekproefomvang

Wat is het nut van het gebruik van standaardfouten?

Wanneer we het gemiddelde van een bepaalde steekproef berekenen, willen we eigenlijk niet het gemiddelde van die specifieke steekproef kennen, maar eerder het gemiddelde van de grotere populatie waaruit de steekproef afkomstig is.

We gebruiken echter steekproeven omdat het veel gemakkelijker is om gegevens voor hen te verzamelen dan voor een hele populatie.

En natuurlijk varieert het steekproefgemiddelde van steekproef tot steekproef, dus gebruiken we de standaardfout van het gemiddelde als een manier om de nauwkeurigheid van onze schatting van het gemiddelde te meten.

U zult in de formule voor het berekenen van de standaardfout opmerken dat naarmate de steekproefomvang (n) toeneemt, de standaardfout afneemt:

Standaardfout = s/ √ n

Dit zou logisch moeten zijn, omdat grotere steekproeven de variabiliteit verminderen en de kans vergroten dat ons steekproefgemiddelde dichter bij het werkelijke populatiegemiddelde ligt.

Wanneer standaardafwijking versus standaardfout gebruiken?

Als we eenvoudigweg de verdeling van waarden in een dataset willen meten, kunnen we standaarddeviatie gebruiken.

Als we echter de onzekerheid rond een schatting van het gemiddelde willen kwantificeren, kunnen we de standaardfout van het gemiddelde gebruiken.

Afhankelijk van uw specifieke scenario en wat u probeert te bereiken, kunt u ervoor kiezen standaarddeviatie of standaardfout te gebruiken.