De standaardfout van een regressiehelling begrijpen

De standaardfout van een regressiehelling is een manier om de „onzekerheid“ bij het schatten van een regressiehelling te meten.

Het wordt als volgt berekend:

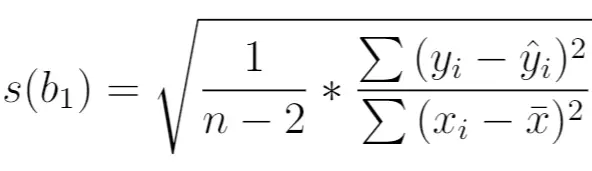
Goud:

• n : totale steekproefomvang
• y _i : reële waarde van de responsvariabele
• ŷ _i : voorspelde waarde van de responsvariabele
• x _i : reële waarde van de voorspellende variabele
• x̄ : gemiddelde waarde van de voorspellende variabele

Hoe kleiner de standaardfout, hoe lager de variabiliteit rond de coëfficiëntschatting voor de regressiehelling.

De standaardfout van de regressiehelling wordt weergegeven in een kolom „standaardfout“ in de regressie-uitvoer van de meeste statistische software:

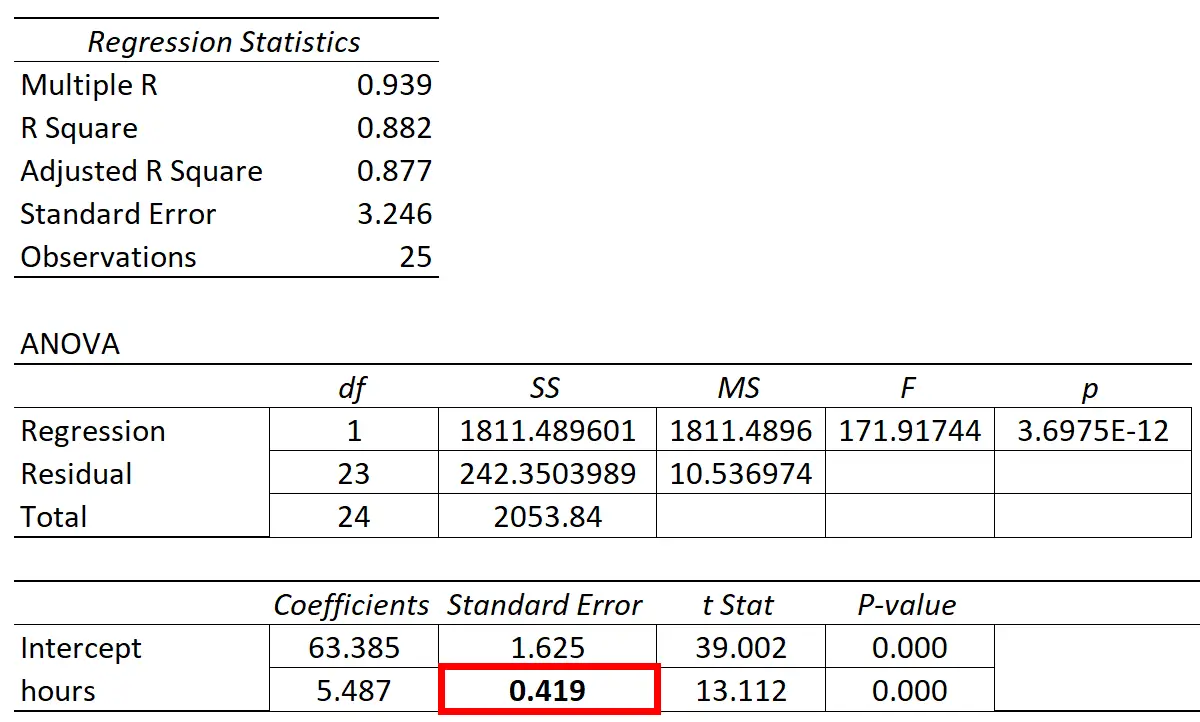
De volgende voorbeelden laten zien hoe u de standaardfout van een regressiehelling in twee verschillende scenario’s interpreteert.

Voorbeeld 1: Interpretatie van een kleine standaardfout van een regressiehelling

Stel dat een hoogleraar inzicht wil krijgen in de relatie tussen het aantal gestudeerde uren en het eindexamencijfer van de leerlingen in zijn klas.

Het verzamelt gegevens voor 25 studenten en creëert het volgende spreidingsdiagram:

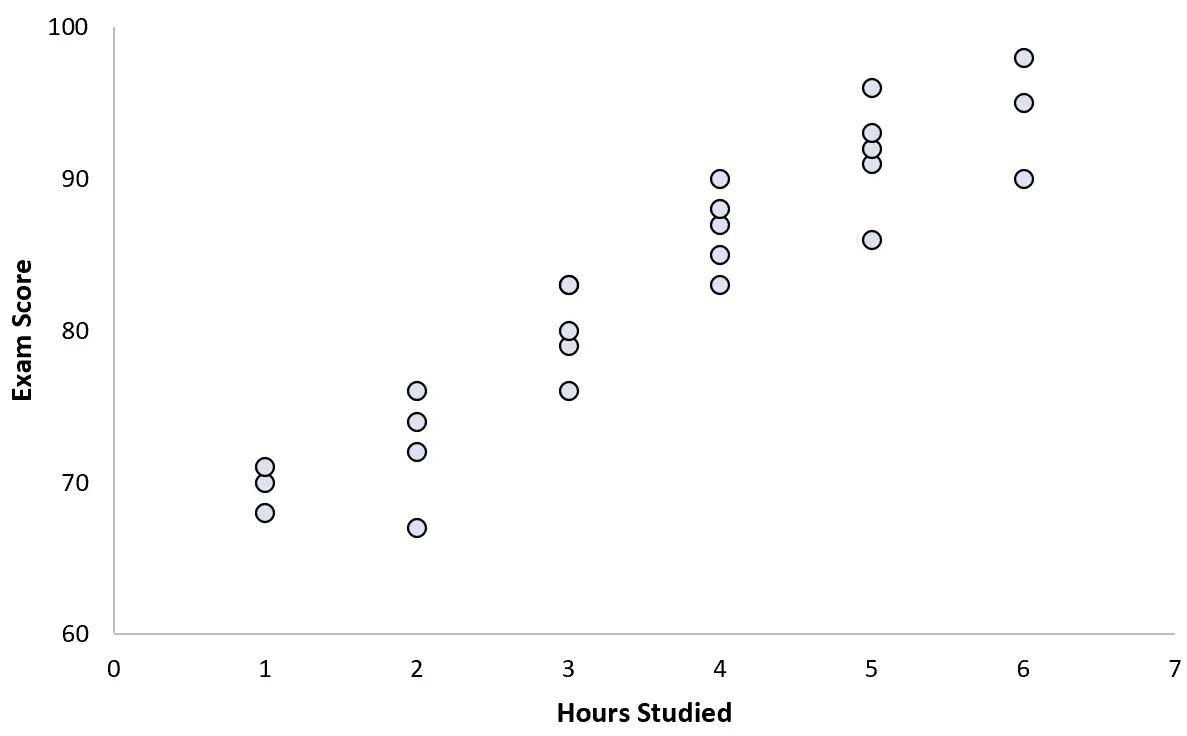
Er is een duidelijk positief verband tussen de twee variabelen. Naarmate het aantal gestudeerde uren toeneemt, stijgt de examenscore in een redelijk voorspelbaar tempo.

Vervolgens paste hij een eenvoudig lineair regressiemodel toe, waarbij hij het aantal bestudeerde uren als voorspellende variabele en het eindexamencijfer als responsvariabele gebruikte.

De volgende tabel toont de regressieresultaten:

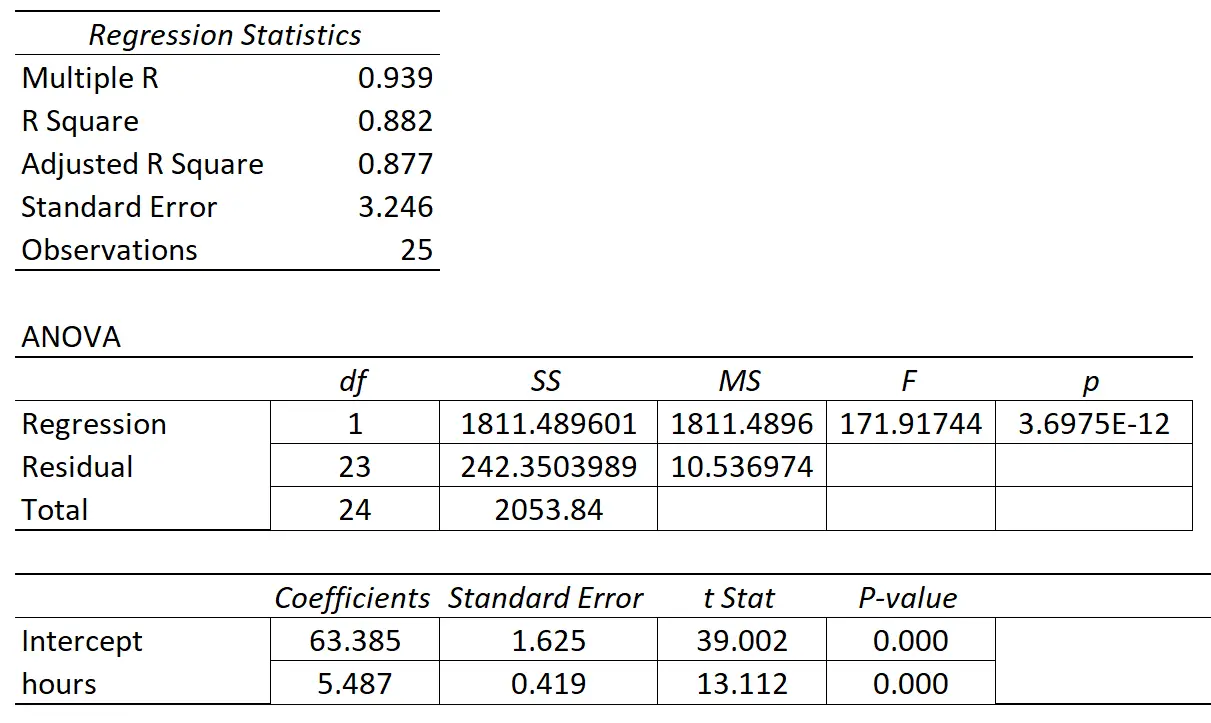
De coëfficiënt van de voorspellende variabele “studie-uren” is 5,487. Dit vertelt ons dat elk extra uur dat wordt gestudeerd, gepaard gaat met een gemiddelde stijging van de examenscore met 5.487 .

De standaardfout is 0,419 , wat een maatstaf is voor de variabiliteit rond deze schatting voor de regressiehelling.

We kunnen deze waarde gebruiken om de t-statistiek voor de voorspellende variabele ‘gestudeerde uren’ te berekenen:

• t-statistiek = coëfficiëntschatting / standaardfout
• t-statistiek = 5,487 / 0,419
• t-statistiek = 13,112

De p-waarde die bij deze toetsstatistiek hoort is 0,000, wat aangeeft dat ‘gestudeerde uren’ een statistisch significante relatie heeft met het eindexamencijfer.

Omdat de standaardfout van de regressiehelling klein was vergeleken met de coëfficiëntschatting van de regressiehelling, was de voorspellende variabele statistisch significant.

Voorbeeld 2: Interpretatie van een grote standaardfout van een regressiehelling

Stel dat een andere hoogleraar inzicht wil krijgen in de relatie tussen het aantal gestudeerde uren en het eindexamencijfer van studenten in zijn klas.

Ze verzamelt gegevens voor 25 leerlingen en maakt het volgende spreidingsdiagram:

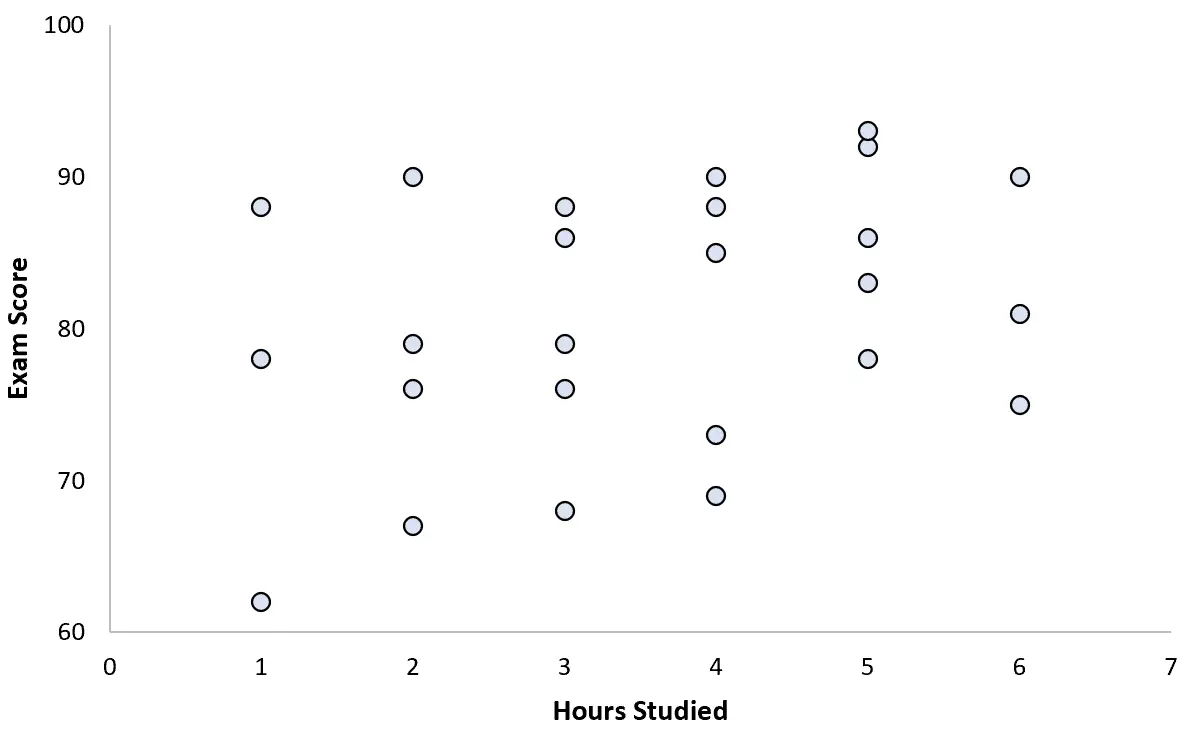
Er lijkt een licht positief verband te bestaan tussen de twee variabelen. Naarmate het aantal studie-uren toeneemt, neemt de examenscore doorgaans toe, maar niet in een voorspelbaar tempo.

Stel dat de professor dan een eenvoudig lineair regressiemodel toepast, met bestudeerde uren als voorspellende variabele en het eindexamencijfer als responsvariabele.

De volgende tabel toont de regressieresultaten:

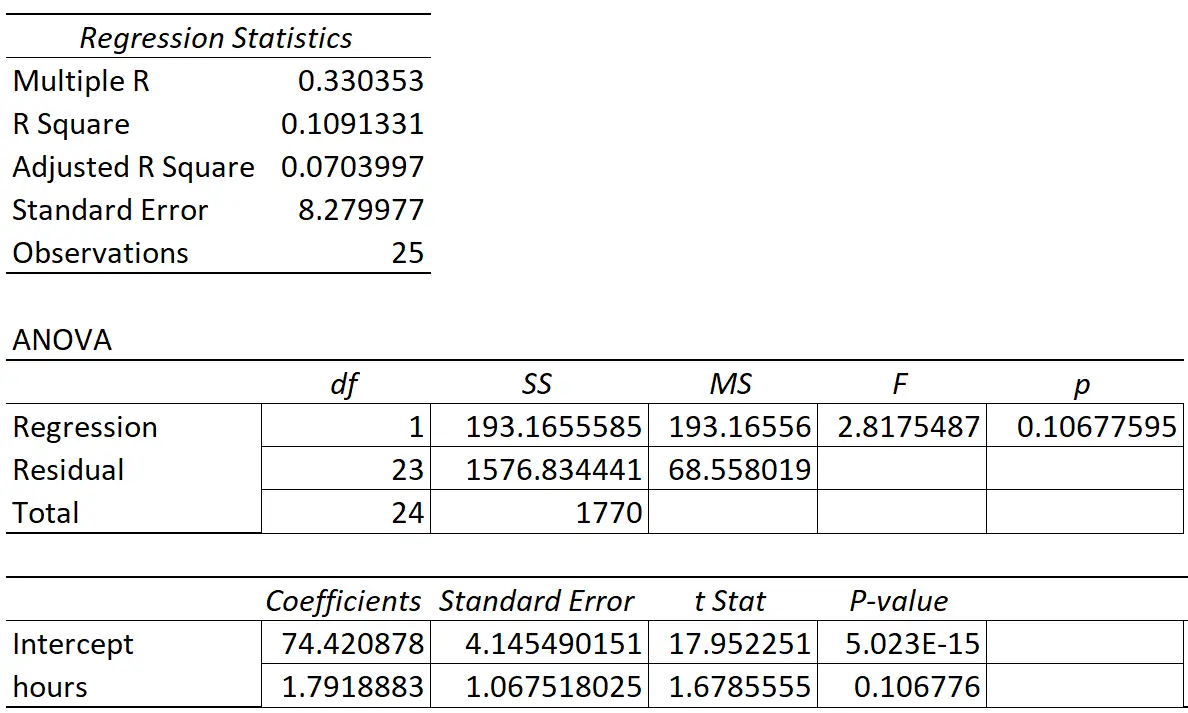
De coëfficiënt van de voorspellende variabele “studie-uren” is 1,7919. Dit vertelt ons dat elk extra uur dat wordt gestudeerd, gepaard gaat met een gemiddelde stijging van 1,7919 in de examenscore.

De standaardfout is 1,0675 , wat een maatstaf is voor de variabiliteit rond deze schatting voor de regressiehelling.

We kunnen deze waarde gebruiken om de t-statistiek voor de voorspellende variabele ‘gestudeerde uren’ te berekenen:

• t-statistiek = coëfficiëntschatting / standaardfout
• t-statistiek = 1,7919 / 1,0675
• t-statistiek = 1,678

De p-waarde die overeenkomt met deze teststatistiek is 0,107. Omdat deze p-waarde niet kleiner is dan 0,05, duidt dit erop dat “uren gestudeerd” geen statistisch significante relatie hebben met het eindexamencijfer.

Omdat de standaardfout van de regressiehelling groot was in verhouding tot de coëfficiëntschatting van de regressiehelling, was de voorspellende variabele niet statistisch significant.

Aanvullende bronnen

Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
Een regressietabel lezen en interpreteren