Wat is een staninescore? (definitie & voorbeelden)

Een Stanine-score , een afkorting van „standaardscore negen“, is een manier om testscores te schalen op een standaardschaal van negen punten.

Met deze methode kunnen we elk testresultaat omzetten van de oorspronkelijke score (dus 0 tot 100) naar een getal tussen 1 en 9.

We gebruiken een eenvoudig proces van twee stappen om de testresultaten aan te passen aan Stanine-scores:

1. Rangschik elk testresultaat van laag naar hoog.

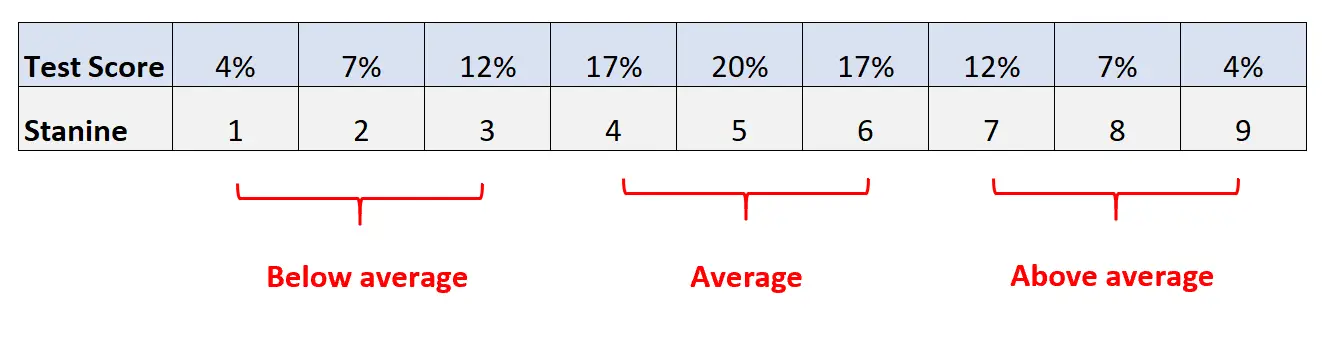
2. Geef de laagste 4% van de scores een staninescore van 1, de daaropvolgende laagste 7% van de scores een staninescore van 2, enzovoort volgens de volgende tabel:

Over het algemeen beschouwen we de testresultaten als volgt:

• Stanines 1, 2, 3: onder het gemiddelde
• Stanines 4, 5, 6: Gemiddeld
• Stanines 7, 8, 9: Bovengemiddeld

Het blijkt dat een Stanine-schaal een gemiddelde van vijf en een standaarddeviatie van twee heeft.

Voor- en nadelen van Stanine-scores

Staninescores bieden de volgende voor- en nadelen:

Voordelen: Dankzij Stanine-scores kunnen we snel begrijpen waar een bepaalde testscore staat in relatie tot alle andere testresultaten.

We weten bijvoorbeeld dat een leerling met een testscore van Stanine 5 in de middelste 20% van alle testscores zit. En we weten dat een leerling die in stanine 9 viel een testscore had in de top 4% van alle scores.

Nadeel: Het nadeel van het gebruik van stanines is dat elke stanine niet dezelfde grootte heeft en dat een testscore in een bepaalde stanine mogelijk dichter bij de scores van de volgende stanine ligt dan de scores van zijn eigen stanine.

Leerlingen die tussen het 40e en 60e percentiel scoren, worden bijvoorbeeld allemaal gegroepeerd in niveau 5. Een leerling wiens testscore in het 58e percentiel ligt, zou echter dichter bij de scores op niveau 6 komen dan de meeste scores. ontvangen in stanine 5.

Stanine Score-alternatieven

Twee alternatieven voor staninescores zijn percentielen en z-scores.

1. Een percentiel vertelt ons het percentage van alle scores waarboven een bepaalde testscore valt.

Een score op het 90e percentiel is bijvoorbeeld hoger dan 90% van alle testscores. Een toetsscore die op het 50e percentiel ligt, ligt precies in het midden van alle toetsscores.

2. Een z-score vertelt ons hoeveel standaardafwijkingen een bepaalde score heeft van het gemiddelde. Het wordt als volgt berekend:

z = (X – μ) / σ

Goud:

• X is een enkele onbewerkte gegevenswaarde
• μ is het gemiddelde van de dataset
• σ is de standaardafwijking van de dataset

We interpreteren z-scores als volgt:

• Een positieve z-score geeft aan dat een testscore bovengemiddeld is
• Een negatieve z-score geeft aan dat een testscore onder het gemiddelde ligt
• Een z-score van nul geeft aan dat de testscore exact gelijk is aan het gemiddelde

Hoe verder een z-score van nul verwijderd is, hoe verder een bepaalde testscore van het gemiddelde verwijderd is.

Z-scores en percentielen geven ons een nauwkeuriger beeld van hoe bepaalde testscores scoren in vergelijking met Stanine-scores.