Stapsgewijze regressie uitvoeren in sas (met voorbeeld)

Stapsgewijze regressie is een procedure die we kunnen gebruiken om een regressiemodel op te bouwen uit een reeks voorspellende variabelen door voorspellers stapsgewijs in het model in te voeren en te verwijderen totdat er geen statistisch geldige reden meer is om voorspellers in te voeren of te verwijderen. verwijder meer.

Het doel van stapsgewijze regressie is het creëren van een regressiemodel dat alle voorspellende variabelen omvat die statistisch significant gerelateerd zijn aan de responsvariabele .

Als u stapsgewijze regressie in SAS wilt uitvoeren, kunt u PROC REG gebruiken met de instructie SELECTION .

In het volgende voorbeeld ziet u hoe u in de praktijk stapsgewijze regressie in SAS kunt uitvoeren.

Voorbeeld: een stapsgewijze regressie uitvoeren in SAS

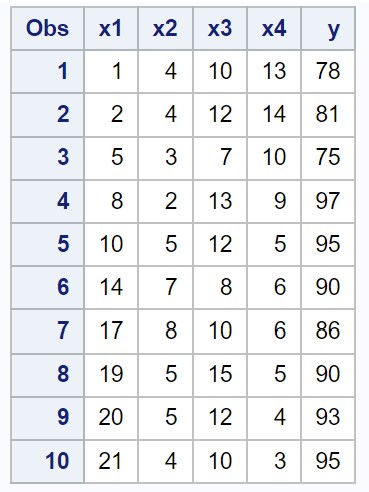
Stel dat we de volgende gegevensset in SAS hebben die vier voorspellende variabelen (x1, x2, x3, x4) en één responsvariabele (y) bevat:

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

Stel nu dat we willen bepalen welke combinatie van voorspellende variabelen het beste meervoudige lineaire regressiemodel zal opleveren.

Als we het hebben over het ‘beste’ regressiemodel, bedoelen we het model dat bepaalde metingen maximaliseert of minimaliseert.

Er zijn twee statistieken die we vaak gebruiken om te evalueren welk regressiemodel het beste is uit een groep potentiële modellen:

1. Aangepaste R-kwadraat : De aangepaste R-kwadraatwaarde vertelt ons het nut van een model, aangepast op basis van het aantal voorspellers in een model. Het model met de hoogste aangepaste R-kwadraatwaarde wordt als het beste beschouwd.

2. AIC : Het Akaike Informatiecriterium (AIC) is een maatstaf die wordt gebruikt om de fit van verschillende regressiemodellen te vergelijken. Het model met de laagste AIC-waarde wordt als het beste beschouwd.

Gelukkig kunnen we zowel de aangepaste R-kwadraat- als de AIC-waarden voor regressiemodellen in SAS berekenen met behulp van PROC REG met de SELECTION- instructie.

De volgende code laat zien hoe u dit doet:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

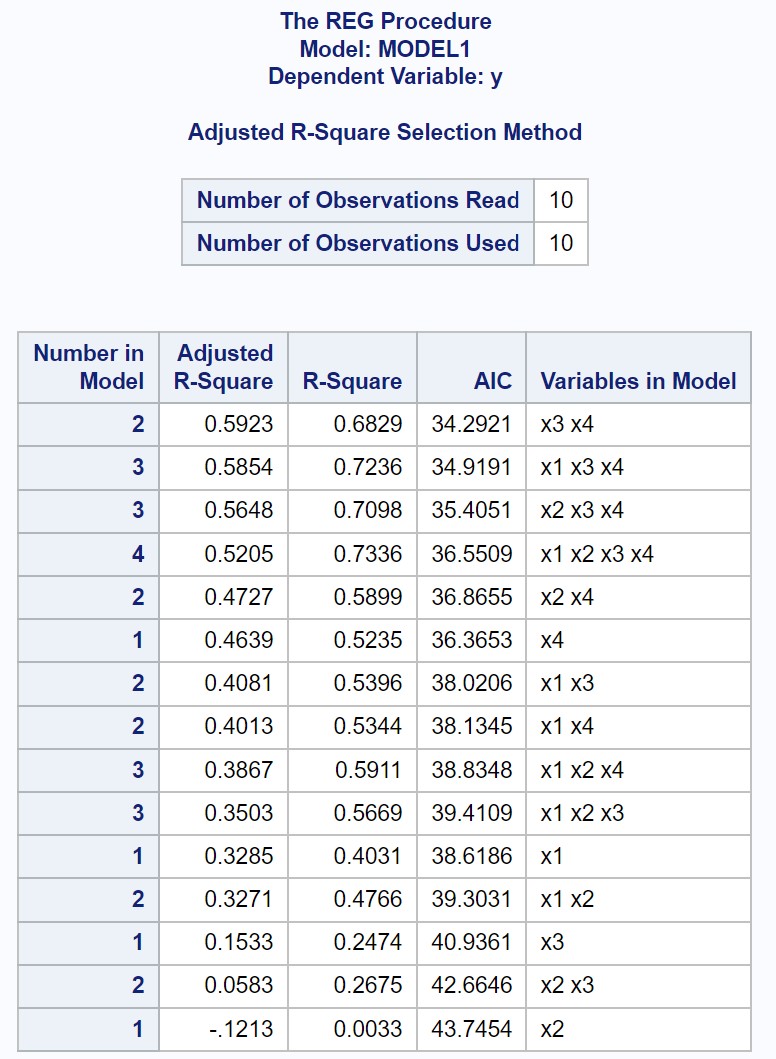
De uitvoer toont de aangepaste R-kwadraat- en AIC-waarden voor elk mogelijk meervoudig lineair regressiemodel.

Uit het resultaat kunnen we zien dat de waarde met de hoogste aangepaste R-kwadraatwaarde en de laagste AIC-waarde het regressiemodel is dat alleen x3 en x4 als voorspellende variabelen gebruikt.

Daarom verklaren wij dat het volgende model „het beste“ is van alle mogelijke modellen:

y = _b0 + _b1 (x3) + _b2 (x4)

Dit specifieke regressiemodel heeft de volgende statistieken:

• Aangepaste R-kwadraatwaarde: 0,5923
• AIC: 34.2921

Opmerkingen over het selecteren van het “beste” regressiemodel

Merk op dat het model met de hoogste aangepaste R-kwadraatwaarde soms niet altijd ook de laagste AIC-waarde heeft.

Als het erom gaat te beslissen welk regressiemodel het beste is, dienen aangepaste R-kwadraat en AIC als suggesties, maar in de echte wereld moet u mogelijk domeinexpertise gebruiken om te bepalen welk model het beste is.

Het kan ook verstandig zijn om een spaarzaam model te kiezen, dat wil zeggen een model dat het gewenste niveau van fit bereikt met zo weinig mogelijk voorspellende variabelen.

De redenering achter dit type model komt voort uit het idee van Occams scheermes (ook wel het ‘parsimony-principe’ genoemd), dat zegt dat de eenvoudigste verklaring waarschijnlijk de juiste is.

Toegepast op statistieken zou een model dat weinig parameters heeft maar een bevredigend niveau van fit bereikt de voorkeur moeten krijgen boven een model dat een heleboel parameters heeft en slechts een iets hoger fitniveau bereikt.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe polynomiale regressie uit te voeren in SAS
Hoe logistische regressie uit te voeren in SAS