Socs: een handig acroniem om distributies te beschrijven

In de statistiek willen we vaak begrijpen hoe een reeks gegevens wordt gedistribueerd. Concreet zijn er vier dingen die handig zijn om te weten over een distributie:

1 . Vorm

• Is de verdeling symmetrisch of scheef naar één kant?
• Is de verdeling unimodaal (één piek) ofbimodaal (twee pieken)?

2. Uitschieters

• Zijn er uitschieters aanwezig in de verdeling?

3. Midden

• Wat is het gemiddelde, de mediaan en de wijze van distributie?

4.Verspreiding

• Wat zijn het bereik, het interkwartielbereik, de standaarddeviatie en de variantie van de verdeling?

SOCS is een handig acroniem dat we kunnen gebruiken om deze vier dingen te onthouden. Het betekent “vorm, uitschieters, centrum, spreiding”.

Laten we een eenvoudig voorbeeld bekijken van hoe u SOCS kunt gebruiken om een distributie te beschrijven.

Voorbeeld: SOCS gebruiken om een distributie te beschrijven

Laten we zeggen dat we de volgende gegevensset hebben die de hoogte toont van een steekproef van twintig verschillende planten.

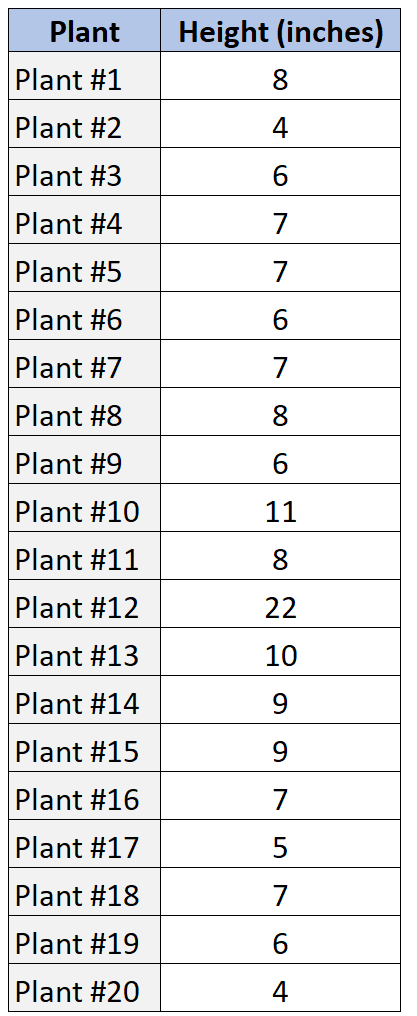
Hier leest u hoe we SOCS kunnen gebruiken om deze verdeling van gegevenswaarden te beschrijven.

Vorm

Eerst willen we de vorm van de verdeling beschrijven.

Een handige manier om de vorm van de verdeling te visualiseren is door een histogram te maken, dat de frequenties van elke waarde in de dataset weergeeft:

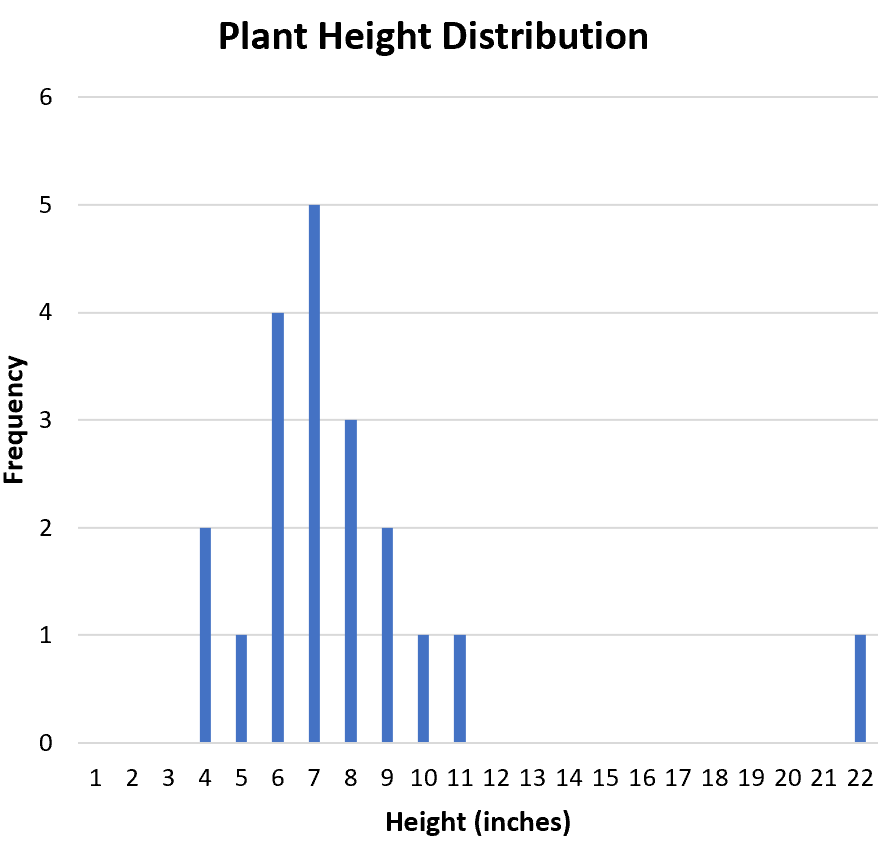
Is de verdeling symmetrisch of scheef naar één kant?   Uit het histogram kunnen we zien dat de verdeling ongeveer symmetrisch is. Met andere woorden: de waarden zijn op de een of andere manier niet bevooroordeeld.

Is de verdeling unimodaal (één piek) of bimodaal (twee pieken)? De verdeling is unimodaal. Het heeft een piek bij de waarde “7”.

Uitschieters

Vervolgens willen we bepalen of er uitbijters in de dataset voorkomen. Aan de hand van het histogram kunnen we de verdeling visueel inspecteren en zien dat 22 mogelijk een uitbijter is:

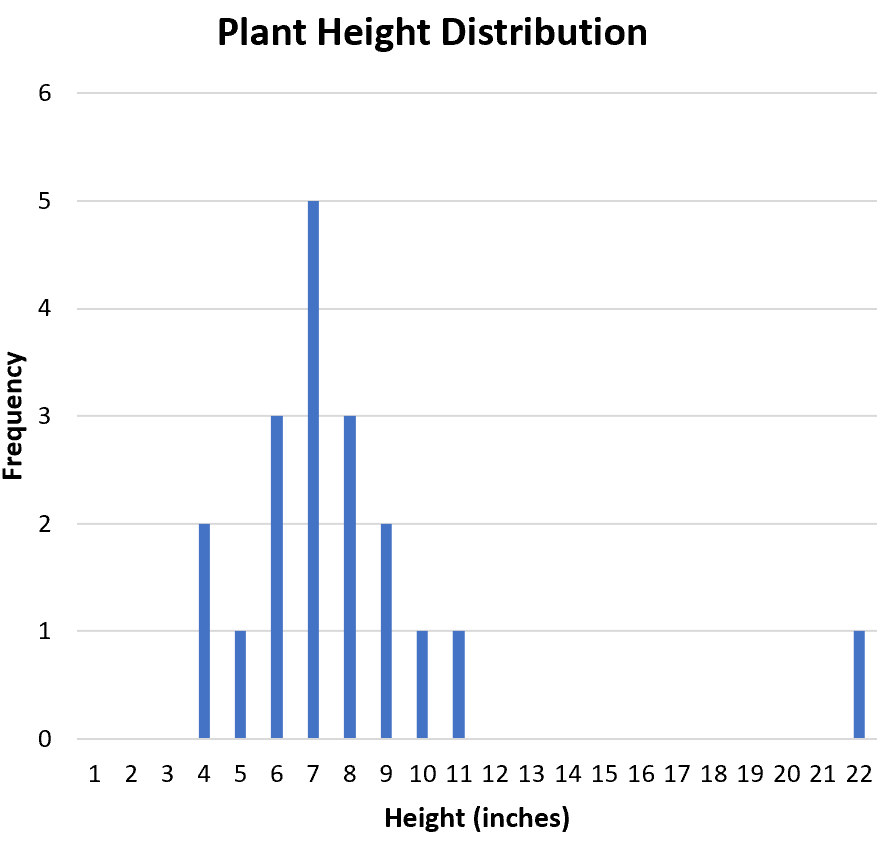
Een gebruikelijke manier om een uitbijter formeel te definiëren is elke waarde die 1,5 keer het interkwartielbereik boven het derde kwartiel of onder het eerste kwartiel ligt.

Met behulp van de interkwartielbereikcalculator kunnen we de 20 ruwe gegevenswaarden invoeren en zien dat het derde kwartiel 9 is, het interkwartielbereik 3 , en daarom is elke waarde groter dan 9 + (1,5*3) = 13,5 een uitschieter. per definitie.

Omdat 22 groter is dan 13,5, kunnen we 22 als een uitbijter beschouwen.

Centrum

Vervolgens willen we beschrijven waar het centrum van de distributie zich bevindt. Drie veelgebruikte maatstaven voor de centrale tendens die we kunnen gebruiken zijn het gemiddelde, de mediaan en de modus.

Gemiddelde: Dit is de gemiddelde waarde van de verdeling. We vinden dit door alle individuele waarden bij elkaar op te tellen en vervolgens te delen door het totale aantal waarden:

Gemiddeld = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Mediaan: Dit is de ‘gemiddelde’ waarde van de verdeling. We vinden dit door alle waarden te ordenen van klein naar groot en vervolgens de mediaanwaarde te identificeren. Het blijken er 7 te zijn.

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Modus: Dit is de waarde die het vaakst voorkomt. Het blijken er 7 te zijn.

Spreiding

Vervolgens willen we de verdeling van waarden in de verdeling beschrijven. Vier veelgebruikte spreidingsmaten die we kunnen gebruiken zijn bereik, interkwartielbereik, standaarddeviatie en variantie.

Bereik: Dit is het verschil tussen de grootste en de kleinste waarde in de dataset. Dit blijkt 22 – 4 = 18 te zijn.

Interkwartielbereik: meet de breedte van de middelste 50% van de gegevenswaarden. Als we de 20 ruwe gegevenswaarden invoeren in de interkwartielbereikcalculator, kunnen we zien dat dit gelijk is aan 3 .

Standaarddeviatie: Dit is een maatstaf voor de gemiddelde verdeling van gegevenswaarden. Als we de 20 ruwe gegevenswaarden invoeren in de variantie- en standaardafwijkingscalculator, kunnen we zien dat de standaardafwijking gelijk is aan 3,69 .

Variantie: Dit is eenvoudigweg de standaarddeviatie, in het kwadraat. Dit is gelijk aan 3,69 ² = 13,63 .

Conclusie

Met behulp van SOCS als leidraad konden we de hoogteverdeling van de plant als volgt beschrijven:

• De verdeling was unimodaal en symmetrisch, wat betekent dat er slechts één piek was en niet scheef naar de ene of de andere kant.
• De verdeling kende één uitschieter: 22.
• De verdeling had een gemiddelde van 7,85, een mediaan van 7 en een modus van 7.
• De verdeling had een bereik van 18, een interkwartielbereik van 3, een standaarddeviatie van 3,69 en een variantie van 13,63.

Merk op dat we SOCS kunnen gebruiken om elke distributie te beschrijven, wat voor ons een nuttige manier is om de vorm van een distributie volledig te begrijpen, of deze uitschieters heeft, waar ongeveer het centrum is en hoe we de waarden Datas moeten distribueren. Zijn.